- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
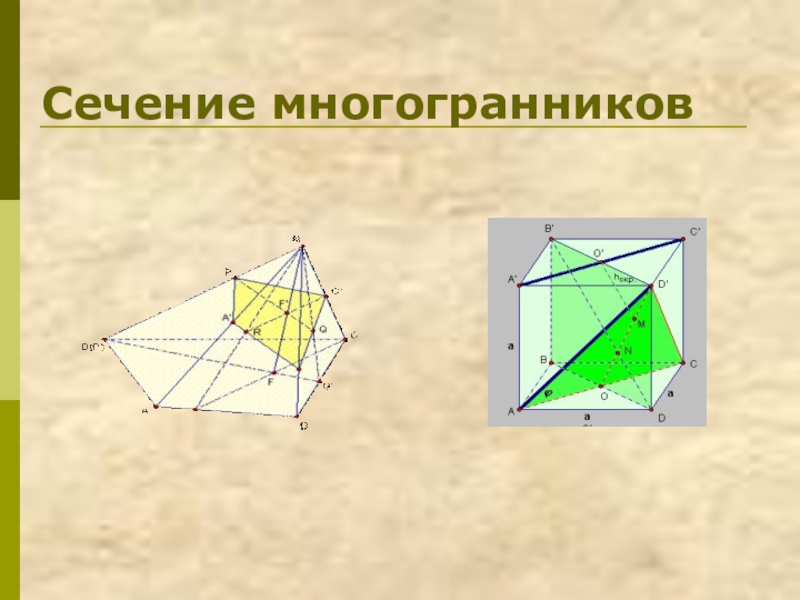
Презентация, доклад по математике на тему Сечение многогранников
Содержание
- 1. Презентация по математике на тему Сечение многогранников
- 2. Многогранником называюттело, поверхность которого состоит из конечного числа плоских многоугольников.Элементы многогранника: вершины, ребра, грани.
- 3. Сечением поверхности геометрических тел называется плоская фигура, полученная
- 4. сечение
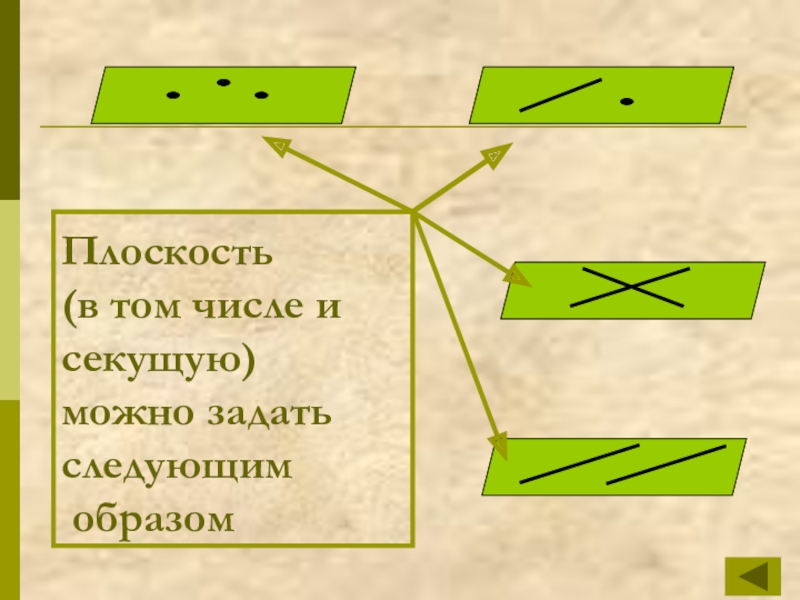
- 5. Плоскость (в том числе и секущую) можно задать следующим образом
- 6. Демонстрация сечений
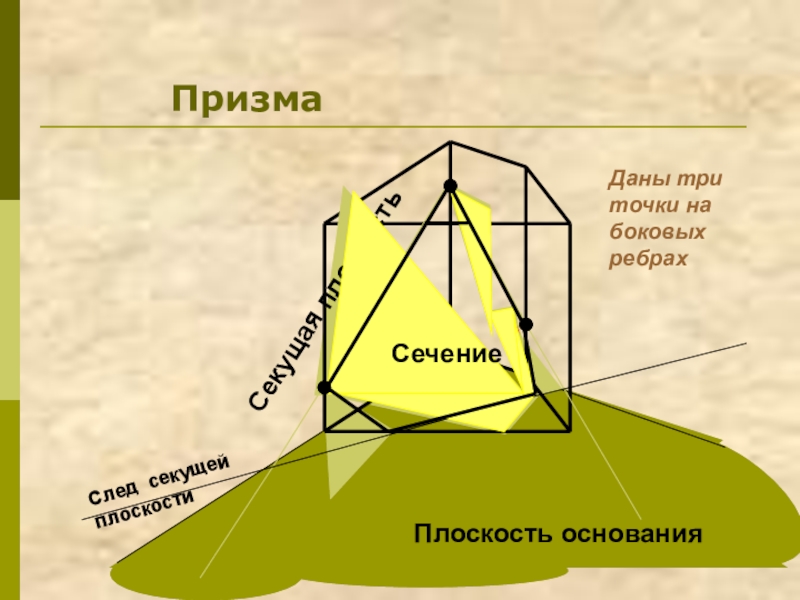
- 7. ПризмаПлоскость основанияСекущая плоскостьДаны три точки на боковых ребрахСечение
- 8. Секущая плоскость пересекает грани многогранника по
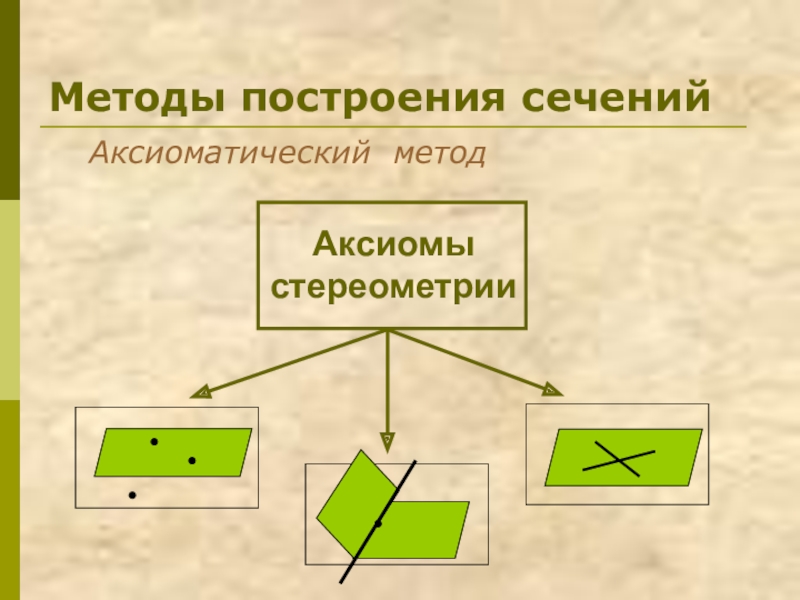
- 9. Методы построения сеченийАксиоматический метод Аксиомы стереометрии
- 10. Аксиоматический метод
- 11. ABCDKLMNFG Проводим через точки F и O
- 12. ABCDKLMNFG Шаг 2: ищем след секущей плоскости
- 13. ABCDKLMNFGШаг 3: делаем разрезы на других
- 14. CBADKLMNFGШаг 4: выделяем сечение многогранника Все разрезы
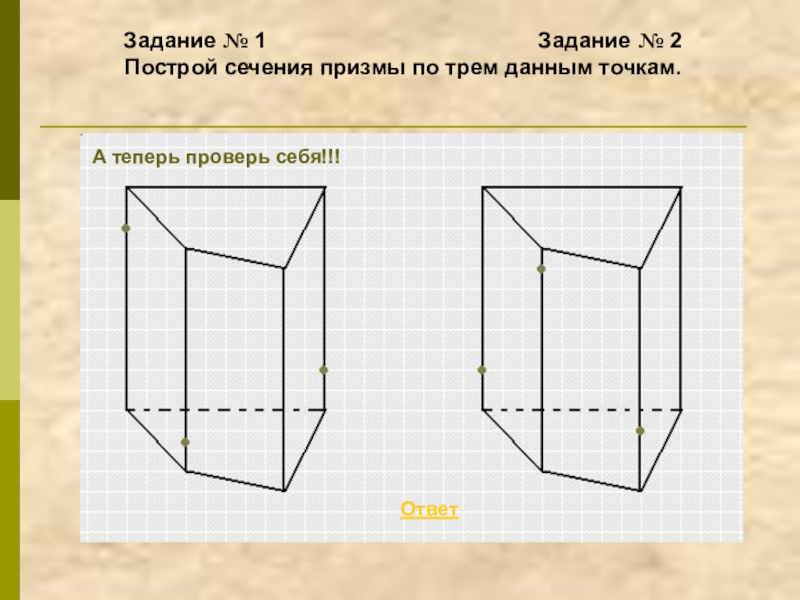
- 15. Задание № 1
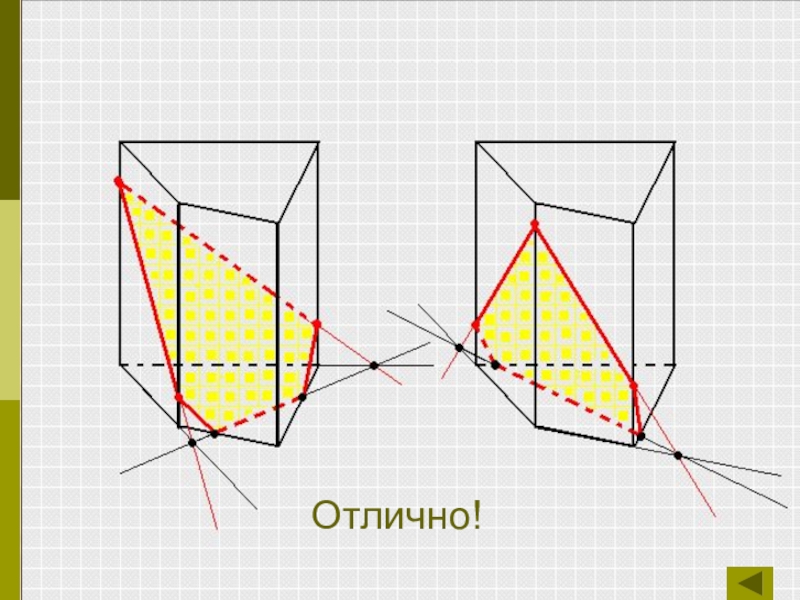
- 16. Отлично!Отлично!
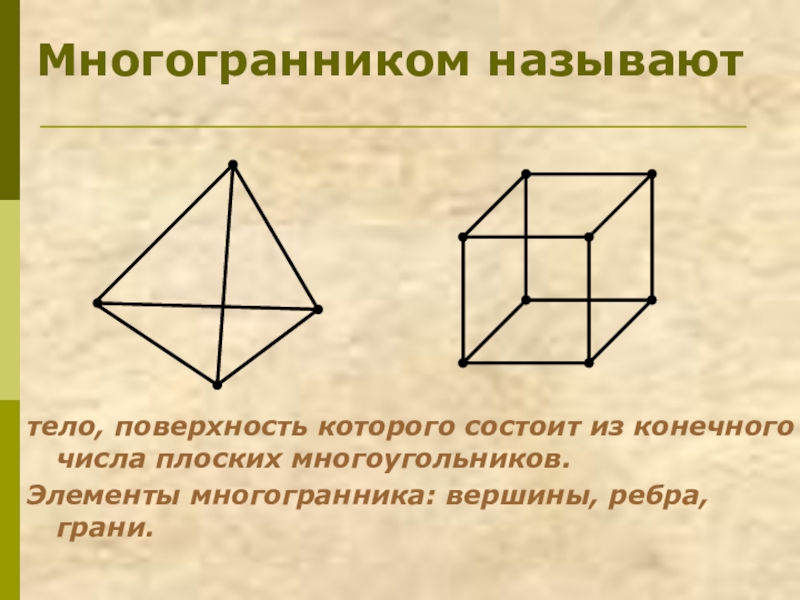
Слайд 2Многогранником называют
тело, поверхность которого состоит из конечного числа плоских многоугольников.
Элементы многогранника:
Слайд 3
Сечением поверхности
геометрических тел называется
плоская фигура, полученная в результате пересечения тела плоскостью
Слайд 8 Секущая плоскость пересекает грани многогранника по прямым, а точнее по
Так как секущая плоскость идет непрерывно, то разрезы образуют замкнутую фигуру-многоугольник.
Полученный таким образом многоугольник и будет сечением тела.
Слайд 10 Аксиоматический метод
Метод следов
Суть метода заключается в построении
Слайд 11
A
B
C
D
K
L
M
N
F
G
Проводим через точки F и O прямую FO.
O
Отрезок FO есть разрез грани KLBA секущей плоскостью.
Аналогичным образом отрезок FG есть разрез грани LMCB.
Постройте сечение призмы, проходящее через точки O,F,G
Шаг 1: разрезаем грани KLBA и LMCB
Слайд 12A
B
C
D
K
L
M
N
F
G
Шаг 2: ищем след секущей плоскости на плоскости основания
Проводим
O
Получим точку H, которая принадлежит и секущей плоскости, и плоскости основания.
Аналогичным образом получим точку R.
Через точки H и R проводим прямую HR – след секущей плоскости
Слайд 13
A
B
C
D
K
L
M
N
F
G
Шаг 3: делаем разрезы на других гранях
Так как прямая
O
Таким образом отрезок ES есть разрез грани ABCD.
Проводим отрезки ОЕ (разрез грани KNDA) и GS (разрез грани MNDC).
Слайд 14C
B
A
D
K
L
M
N
F
G
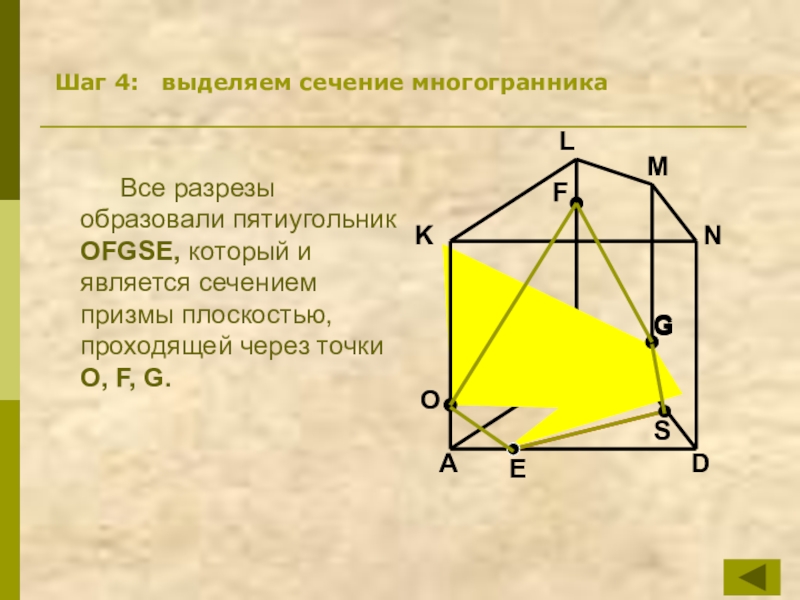
Шаг 4: выделяем сечение многогранника
Все разрезы образовали пятиугольник OFGSE, который
O
G
Слайд 15Задание № 1
Ответ
А теперь проверь себя!!!