- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
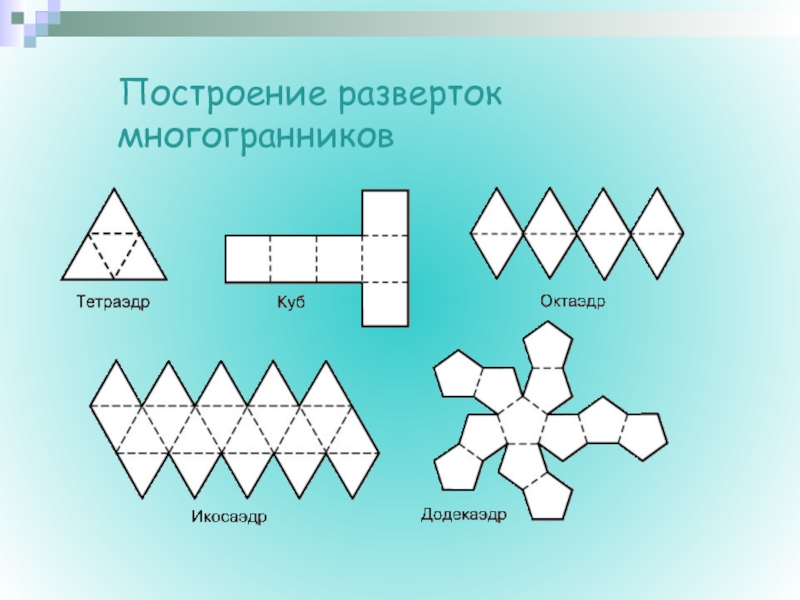
Презентация, доклад на тему многогранники.
Содержание
- 1. многогранники.
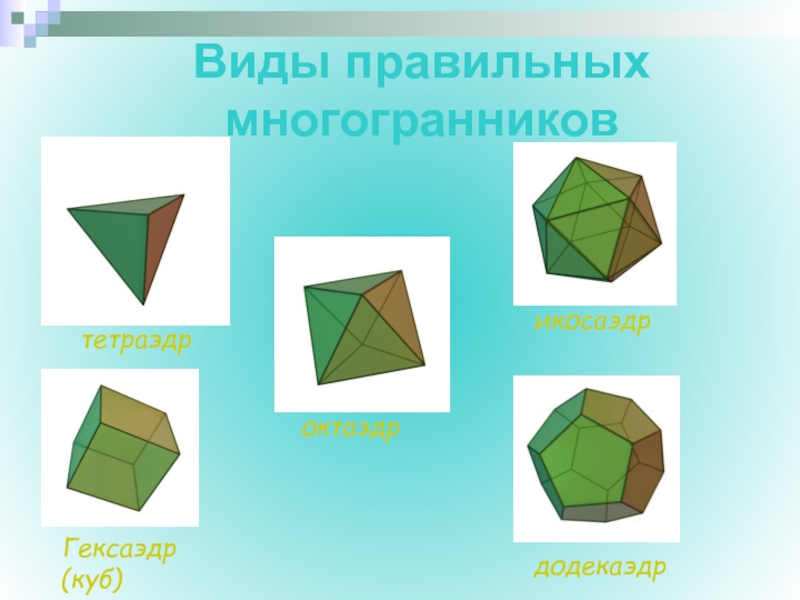
- 2. Виды правильных многогранниковтетраэдроктаэдрикосаэдрГексаэдр (куб)додекаэдр
- 3. Определение многогранника: Многогранник – это часть пространства,
- 4. Правильным называется многогранник, у которого все грани
- 5. Многогранник называется правильным, если:он выпуклыйвсе его грани
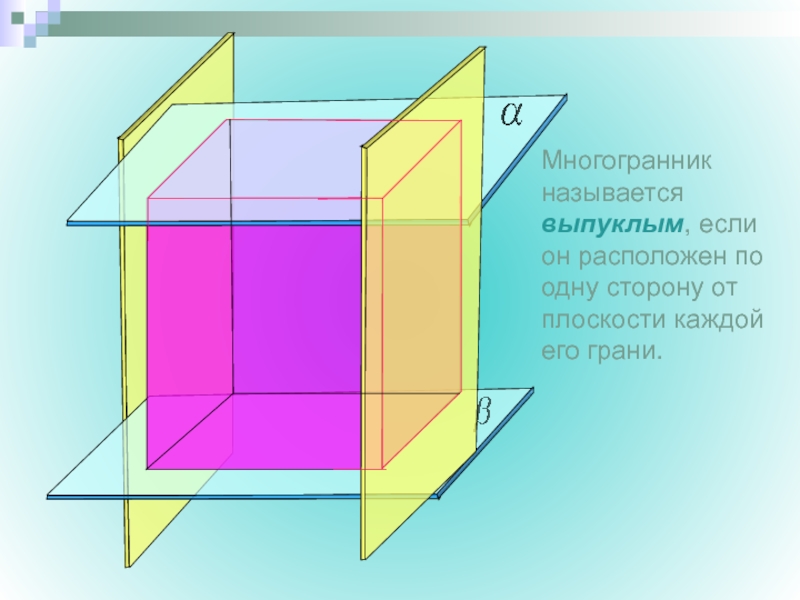
- 6. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
- 7. Слайд 7
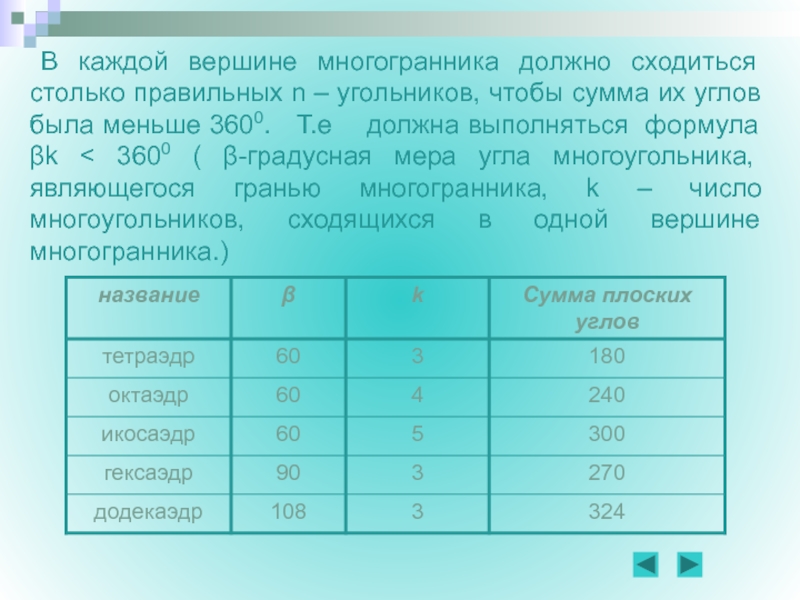
- 8. В каждой вершине многогранника должно сходиться
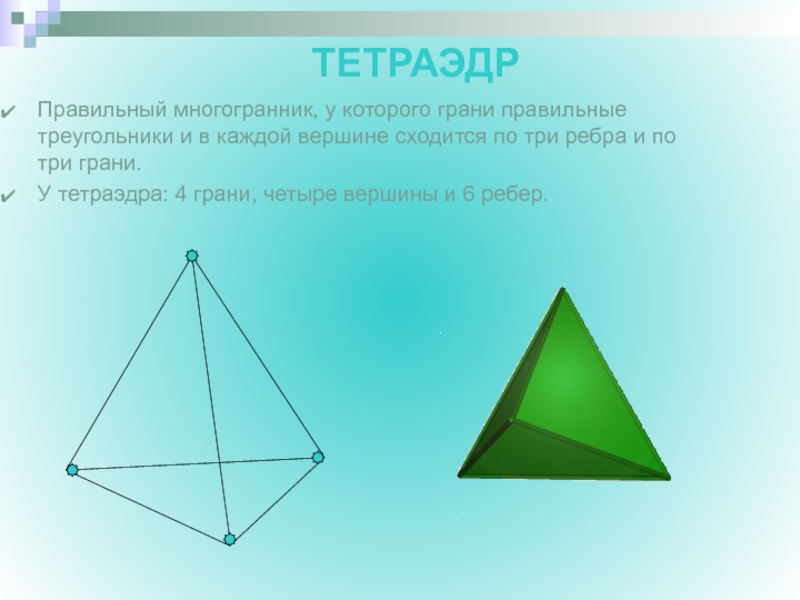
- 9. Правильный многогранник, у которого грани правильные треугольники
- 10. ОКТАЭДРПравильный многогранник, у которого грани- правильные
- 11. ИКОСОЭДРПравильный многогранник, у которого грани - правильные
- 12. КУБ Правильный многогранник, у которого грани –
- 13. ДОДЕКАЭДРПравильный многогранник,
- 14. Площадь поверхности .Объём.
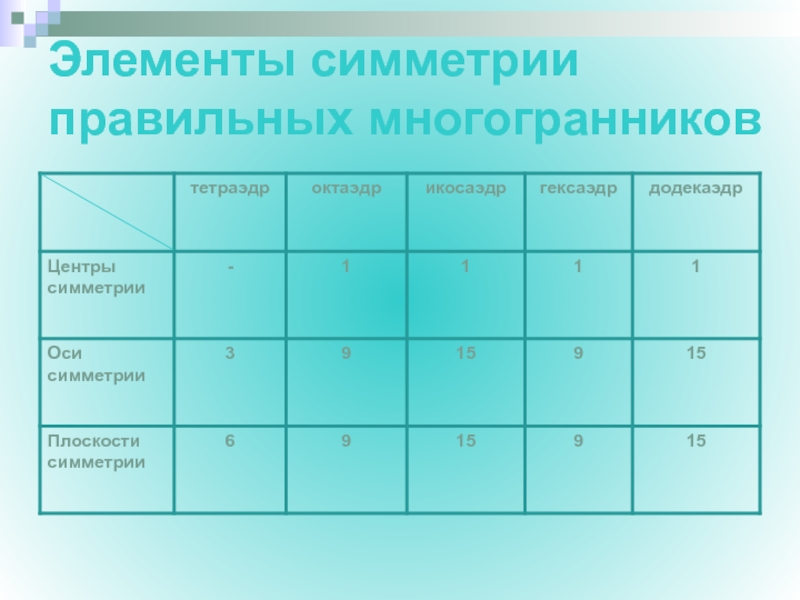
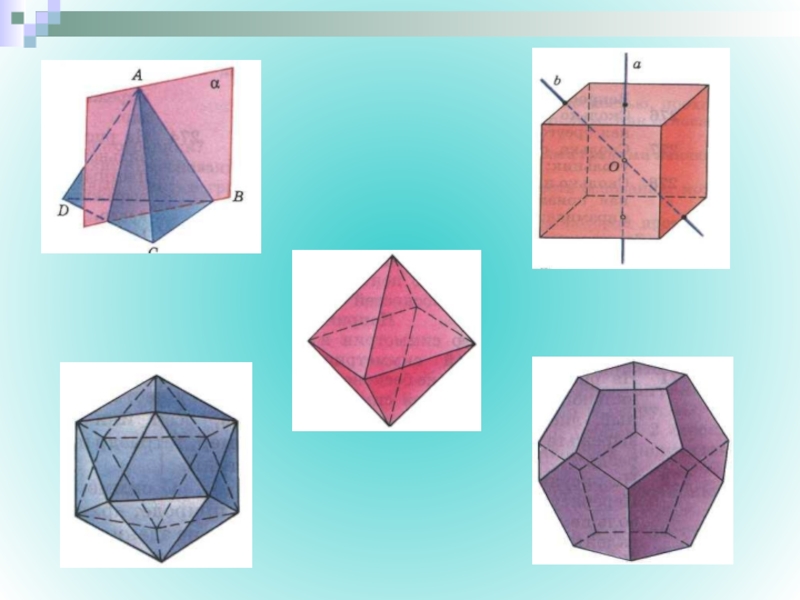
- 15. Элементы симметрии правильных многогранников
- 16. Слайд 16
- 17. Построение разверток многогранников
- 18. Немного историиВсе типы правильных многогранников были известны
- 19. Правильные многогранники называют также «платоновыми телами» -
- 20. Тела АрхимедаАрхимедовыми телами называются полуправильные однородные выпуклые
- 21. Тела Архимеда
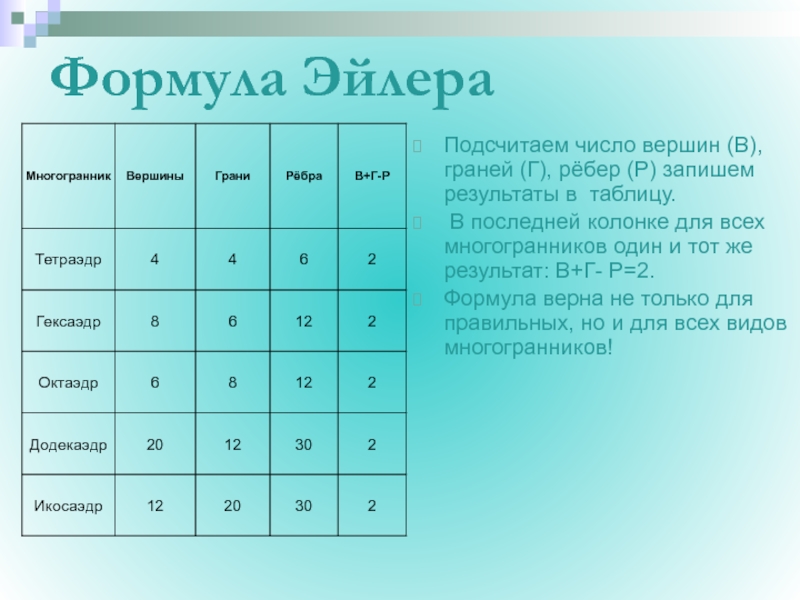
- 22. Формула ЭйлераПодсчитаем число вершин (В), граней (Г),
- 23. Построение многогранников с помощью куба.
- 24. “ Закон взаимности ”У правильных многогранников есть
- 25. Центры граней додекаэдра являются вершинами икосаэдра, а центры граней икосаэдра – вершинами додекаэдра.
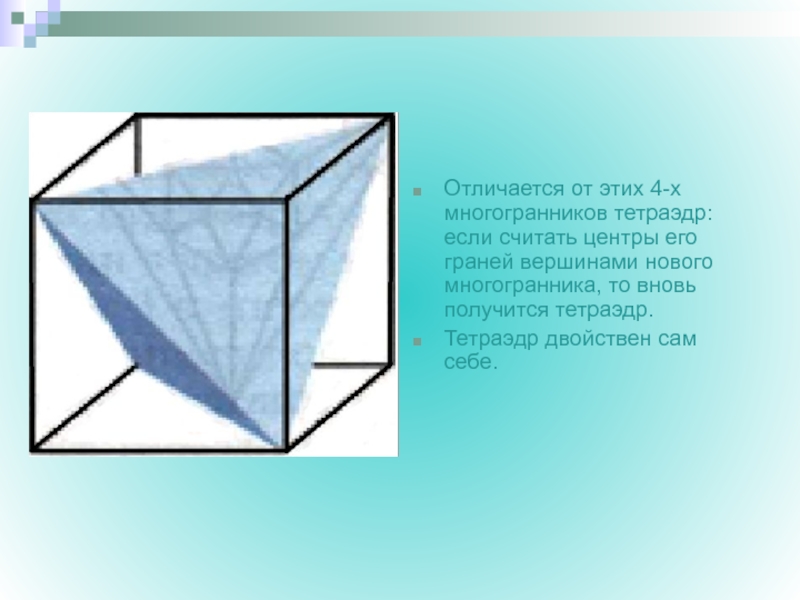
- 26. Отличается от этих 4-х многогранников тетраэдр: если
- 27. Куб и октаэдр, додекаэдр и икосаэдр –
- 28. С1В1АПостроение правильного тетраэдра вписанного в кубРассмотрим вершину
- 29. Построение правильного тетраэдра
- 30. Построение правильного октаэдра, вписанного в данный кубВыбираем
- 31. Описать около данного куба правильный октаэдрЧерез центры
- 32. Построение икосаэдра, вписанного в кубПоместим на средних
- 33. На каждой грани куба строим « четырехскатную
Виды правильных многогранниковтетраэдроктаэдрикосаэдрГексаэдр (куб)додекаэдр
Слайд 3
Определение многогранника:
Многогранник – это часть пространства, ограниченная совокупностью конечного числа
плоских многоугольников, соединённых таким образом, что каждая сторона любого многогранника является стороной ровно одного многоугольника. Многоугольники называются гранями, их стороны – рёбрами, а вершины – вершинами.
Слайд 4
Правильным называется многогранник, у которого все грани являются правильными многоугольниками, и
все многогранные углы при вершинах равны.
Пример правильного многогранника (икосаэдр), его гранями являются правильные (равносторонние) треугольники.
Слайд 5Многогранник называется правильным, если:
он выпуклый
все его грани являются равными правильными многоугольниками
в
каждой его вершине сходится одинаковое число граней
все его двугранные углы равны
все его двугранные углы равны
Слайд 6
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости
каждой его грани.
Слайд 8
В каждой вершине многогранника должно сходиться столько правильных n –
угольников, чтобы сумма их углов была меньше 3600. Т.е должна выполняться формула βk < 3600 ( β-градусная мера угла многоугольника, являющегося гранью многогранника, k – число многоугольников, сходящихся в одной вершине многогранника.)
Слайд 9
Правильный многогранник, у которого грани правильные треугольники и в каждой вершине
сходится по три ребра и по три грани.
У тетраэдра: 4 грани, четыре вершины и 6 ребер.
У тетраэдра: 4 грани, четыре вершины и 6 ребер.
ТЕТРАЭДР
Слайд 10
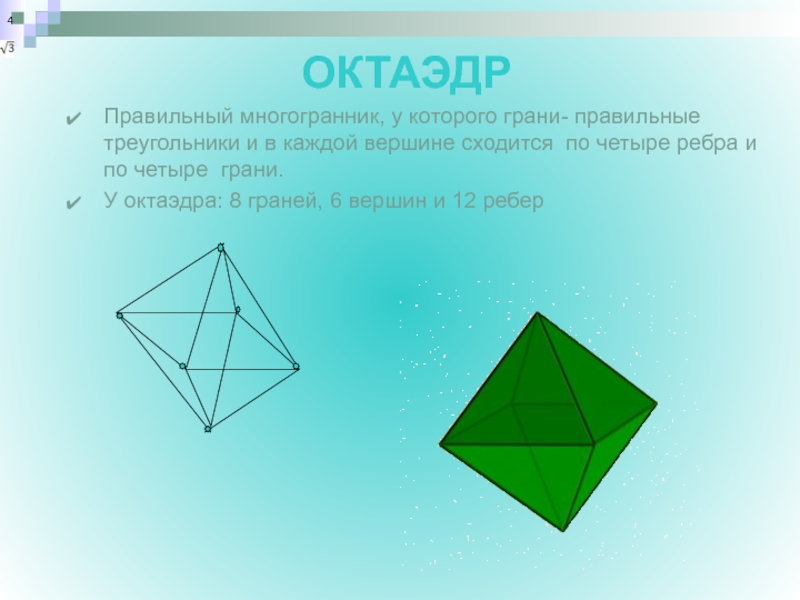
ОКТАЭДР
Правильный многогранник, у которого грани- правильные треугольники и в каждой
вершине сходится по четыре ребра и по четыре грани.
У октаэдра: 8 граней, 6 вершин и 12 ребер
У октаэдра: 8 граней, 6 вершин и 12 ребер
4
Слайд 11
ИКОСОЭДР
Правильный многогранник, у которого грани - правильные треугольники и в вершине
сходится по пять рёбер и граней.
У икосаэдра:20 граней, 12 вершин и 30 ребер
У икосаэдра:20 граней, 12 вершин и 30 ребер
Слайд 12
КУБ
Правильный многогранник, у которого грани – квадраты и в каждой
вершине сходится по три ребра и три грани.
У него: 6 граней, 8 вершин и 12 ребер.
У него: 6 граней, 8 вершин и 12 ребер.
Слайд 13
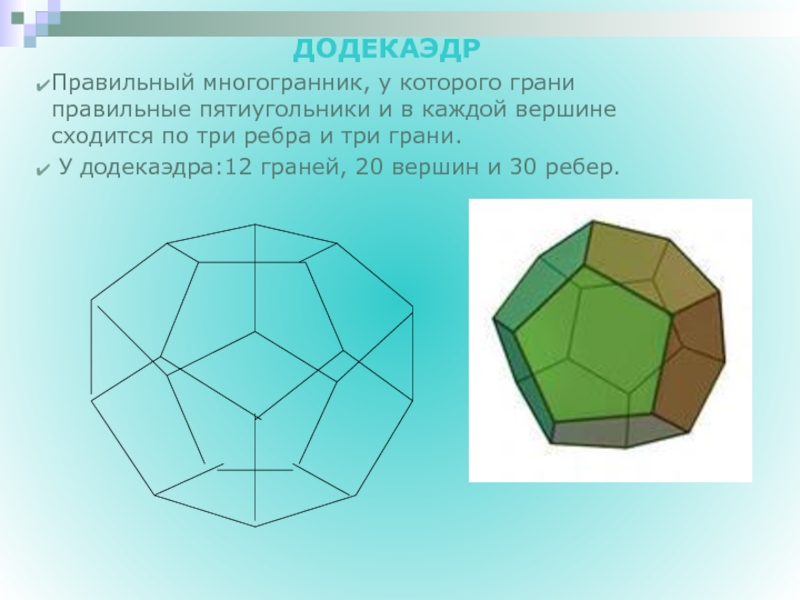
ДОДЕКАЭДР
Правильный многогранник, у которого грани правильные
пятиугольники и в каждой вершине сходится по три ребра и три грани.
У додекаэдра:12 граней, 20 вершин и 30 ребер.
У додекаэдра:12 граней, 20 вершин и 30 ребер.
Слайд 18
Немного истории
Все типы правильных многогранников были известны в Древней Греции –
именно им посвящена завершающая, XIII книга «Начала» Евклида.
Слайд 19
Правильные многогранники называют также «платоновыми телами» - они занимали видное место
в идеалистической картине мира древнегреческого философа Платона.
Додекаэдр символизировал всё мироздание, почитался главнейшим. Уже по латыни в средние века его стали называть «пятая сущность» или guinta essentia, «квинта эссенциа», отсюда происходит вполне современное слово «квинтэссенция», означающее всё самое главное, основное, истинную сущность чего-либо.
Слайд 20Тела Архимеда
Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые
многогранники, все многогранные углы которых равны, а грани - правильные многоугольники нескольких типов.
Слайд 22Формула Эйлера
Подсчитаем число вершин (В), граней (Г), рёбер (Р) запишем результаты
в таблицу.
В последней колонке для всех многогранников один и тот же результат: В+Г- Р=2.
Формула верна не только для правильных, но и для всех видов многогранников!
В последней колонке для всех многогранников один и тот же результат: В+Г- Р=2.
Формула верна не только для правильных, но и для всех видов многогранников!
Слайд 24
“ Закон взаимности ”
У правильных многогранников есть интересная особенность – своеобразный
,,Закон взаимности”. Центры граней куба являются вершинами октаэдра, а центры граней октаэдра – вершинами куба.
Слайд 25
Центры граней додекаэдра являются вершинами икосаэдра, а центры граней икосаэдра –
вершинами додекаэдра.
Слайд 26
Отличается от этих 4-х многогранников тетраэдр: если считать центры его граней
вершинами нового многогранника, то вновь получится тетраэдр.
Тетраэдр двойствен сам себе.
Тетраэдр двойствен сам себе.
Слайд 27
Куб и октаэдр, додекаэдр и икосаэдр – это две пары двойственных
многогранников. У них одинаковое число рёбер (12 – у куба и октаэдра; 30 – у додекаэдра и икосаэдра), а числа вершин и граней переставлены.
Слайд 28
С1
В1
А
Построение правильного тетраэдра вписанного в куб
Рассмотрим вершину куба А. В ней
сходятся три грани куба, имеющие форму квадратов. В каждом из этих квадратов берем вершину противоположную А,- вершины куба В1, С1, D. Точки А, В1,С1, D- являются вершинами правильного тетраэдра.
D
Слайд 30
Построение правильного октаэдра, вписанного в данный куб
Выбираем куб. В нем последовательно
проводим отрезки: слабо видимыми линиями соединяем попарно между собой вершины каждой грани. Точки пересечения этих диагоналей соединяем между собой.
Слайд 31
Описать около данного куба правильный октаэдр
Через центры противоположных
граней куба проведем
прямые,
которые пересекаются в точке О- центре куба- и являются взаимно перпендикулярными. На каждой из этих прямых по обе стороны от точки О отложим отрезки длиной 1,5 а,
Где а- длина ребра куба. Концы этих отрезков являются вершинами правильного октаэдра. Далее последовательно соединяем эти вершины.
которые пересекаются в точке О- центре куба- и являются взаимно перпендикулярными. На каждой из этих прямых по обе стороны от точки О отложим отрезки длиной 1,5 а,
Где а- длина ребра куба. Концы этих отрезков являются вершинами правильного октаэдра. Далее последовательно соединяем эти вершины.
O
Слайд 32
Построение икосаэдра, вписанного в куб
Поместим на средних линиях граней куба по
одному отрезку одинаковой длины с концами на равных расстояниях от ребер. Расположим отрезки и выберем их длину так, чтобы соединяя концы отрезка одной грани с концом отрезка другой грани получить равносторонний треугольник, причем из каждой вершины должны выходить пять ребер.
Слайд 33
На каждой грани куба строим « четырехскатную крышу», две грани которой-
треугольники и две- трапеции. Такие треугольник и трапецию получим, если построим правильный пятиугольник, у которого диагональ равна ребру куба. Стороны этого пятиугольника будут равны ребрам додекаэдра, а построенные с помощью диагонали треугольник и трапеция окажутся фрагментами «четырехскатной крыши»
Построение додекаэдра, описанного около куба
