- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Правильные многоугольники
Содержание
- 1. Презентация по математике на тему Правильные многоугольники
- 2. Цель работыЦель работы:рассказать про правильные многогранники которые
- 3. Правильным многогранником называется многогранник, у которого все
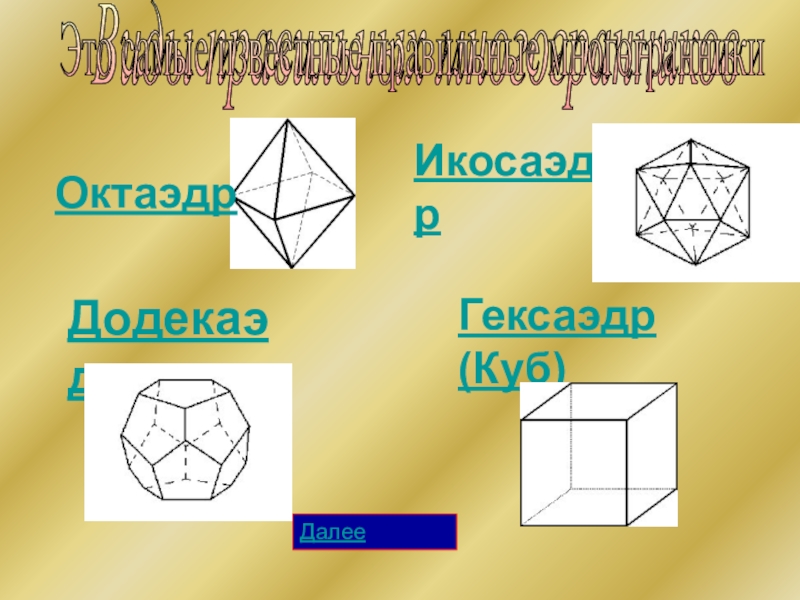
- 4. Виды правильных многогранниковОктаэдрДодекаэдрИкосаэдрГексаэдр (Куб)Это самые известные правильные многогранники Далее
- 5. Октаэдр является вершиной четырех треугольников. Сумма плоских
- 6. ДодекаэдрДодекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая
- 7. Икосаэдр составлен из двадцати равносторонних треугольников. Каждая
- 8. Гексаэдр (Куб)Куб составлен из шести квадратов. Каждая
- 9. Из моей галлереи!
- 10. Слайд 10
- 11. Слайд 11
- 12. Спасибо за внимание!!! Надеюсь вам понравилось и вы заинтересуетесь этой темой, как ЯАвтор
Слайд 1Проект по геометрии"правильные многогранники"
Выполнил: ученик 8а
класса МОУ «КСОШ»
Степанов Афанасий
Слайд 2Цель работы
Цель работы:рассказать про правильные многогранники которые очень заинтересовали меня и
Ещё хочу научиться использовать программы Microsoft Office Word и Microsoft PowerPoint и пользоваться Интернетом.
Слайд 3Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники,
но есть и такие многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные правильные многоугольники. Многогранники такого типа называются равноугольно полуправильными многогранниками. Впервые многогранники такое типа открыл Архимед. Им подробно описаны 13 многогранников, которые позже в честь великого ученого были названы телами Архимеда.
Правильные многогранники
Многогранник называется правильным, если:
1. он выпуклый
2. все его грани являются
равными правильными
многоугольниками
3.в каждой его вершине сходится
одинаковое число рёбер
Слайд 4Виды правильных многогранников
Октаэдр
Додекаэдр
Икосаэдр
Гексаэдр (Куб)
Это самые известные правильные многогранники
Далее
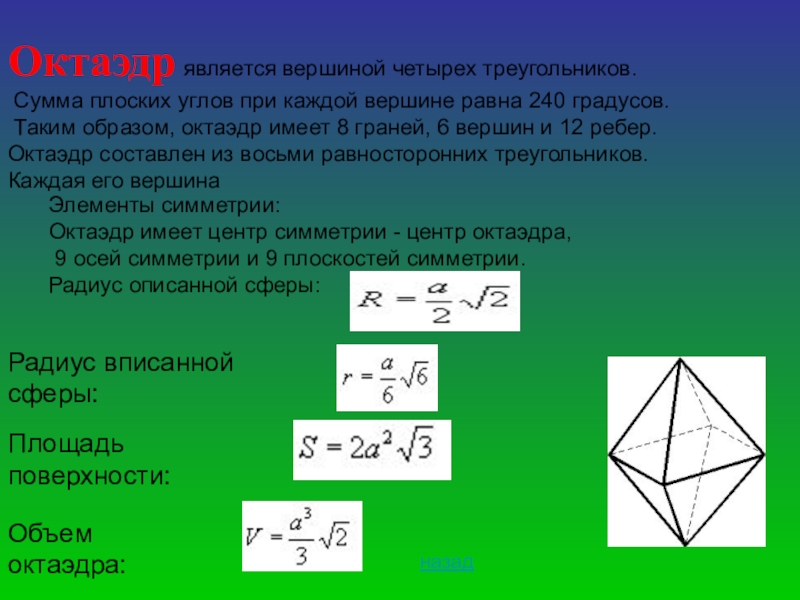
Слайд 5Октаэдр является вершиной четырех треугольников.
Сумма плоских углов при каждой вершине
Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.
Октаэдр составлен из восьми равносторонних треугольников.
Каждая его вершина
Элементы симметрии:
Октаэдр имеет центр симметрии - центр октаэдра,
9 осей симметрии и 9 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем октаэдра:
назад
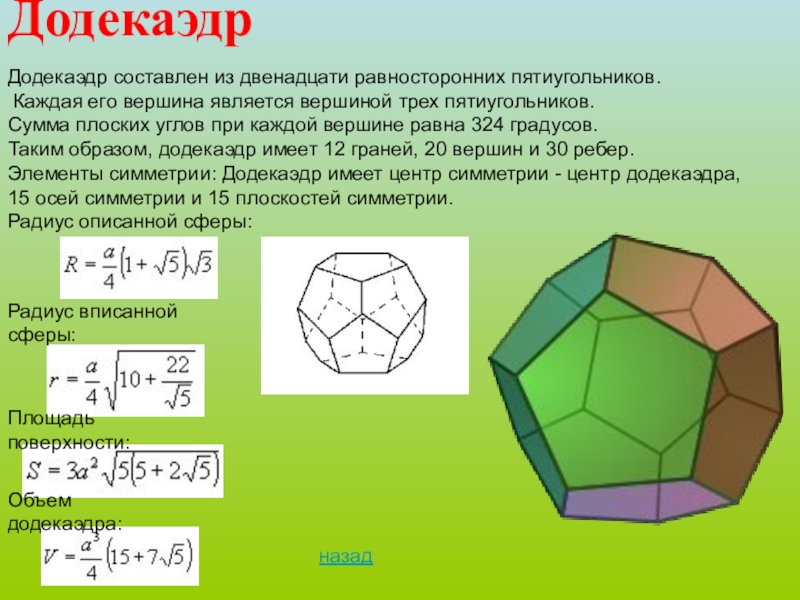
Слайд 6Додекаэдр
Додекаэдр составлен из двенадцати равносторонних пятиугольников.
Каждая его вершина является вершиной
Сумма плоских углов при каждой вершине равна 324 градусов.
Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
Элементы симметрии: Додекаэдр имеет центр симметрии - центр додекаэдра,
15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем додекаэдра:
назад
Слайд 7Икосаэдр составлен из двадцати равносторонних треугольников.
Каждая его вершина является вершиной
Сумма плоских углов при каждой вершине равна 300 градусов.
Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
Элементы симметрии:
Икосаэдр имеет центр симметрии - центр икосаэдра,
15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем икосаэдра:
Икосаэдр
назад
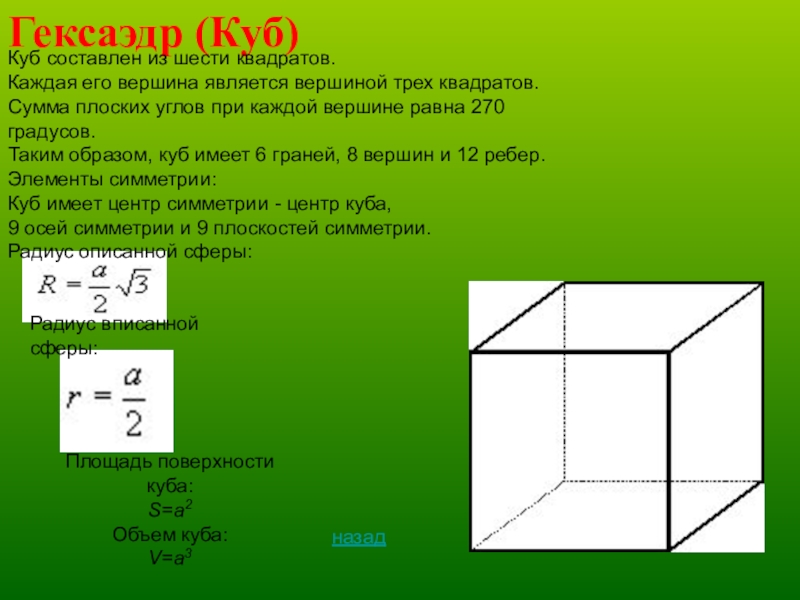
Слайд 8Гексаэдр (Куб)
Куб составлен из шести квадратов.
Каждая его вершина является вершиной
Сумма плоских углов при каждой вершине равна 270 градусов.
Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер.
Элементы симметрии:
Куб имеет центр симметрии - центр куба,
9 осей симметрии и 9 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности куба:
S=a2
Объем куба:
V=a3
назад