- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Подобие фигур (9 класс)
Содержание
- 1. Презентация по математике на тему Подобие фигур (9 класс)
- 2. Что есть подобие? Искусство изображать
- 3. О подобииОдинаковые по форме, но различные по
- 4. ИЗ ИСТОРИИ ПОДОБИЯИдея отношения и Пропорции зародилась
- 5. Преобразование подобия. Определение преобразования подобия одинаково
- 6. Подобие треугольников
- 7. Признаки подобияПервый признак – по двум углам.Второй
- 8. Первый признакЕсли два угла одного треугольника соответственно
- 9. Второй признакЕсли две стороны одного треугольника пропорциональны
- 10. Третий признакЕсли три стороны одного треугольника пропорциональны
- 11. Докажите, что треугольники подобны
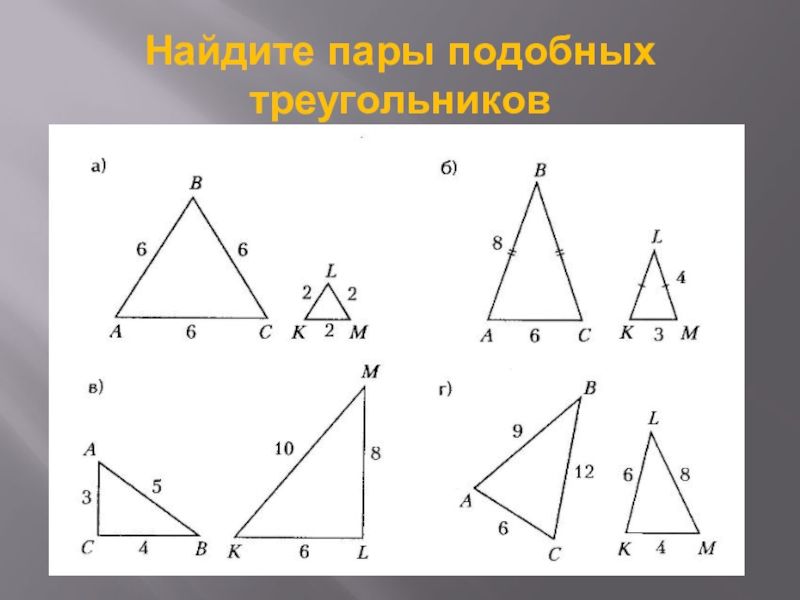
- 12. Найдите пары подобных треугольников
Что есть подобие? Искусство изображать предметы на плоскости с Древних времён привлекает к себе внимание человека. Люди рисовали на скалах, стенах, сосудах и прочих предметах быта, различные орнаменты, растения, животных. Люди стремились к тому,
Слайд 2Что есть подобие?
Искусство изображать предметы на плоскости с
Древних времён привлекает к себе внимание человека. Люди рисовали на скалах, стенах, сосудах и прочих предметах быта, различные орнаменты, растения, животных. Люди стремились к тому, чтобы изображение правильно отображало естественную форму предмета . Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в IV-V веках до нашей эры и существует до сих пор. Например, очень много детских игрушек подобным предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию. Понятие подобия, наряду с понятием движения, является одним из важных понятий геометрии. Оно имеет большое образовательное и практическое значение. Подобие используется при определении расстояний до недоступных предметов, в устройствах различных измерительных инструментов и приборов. В настоящее время существует большое количество методической литературы по изучению в средней школе, как геометрии, так и подобных треугольников в частности. В основном они построены на известных опробованных учебниках, так как во всех учебных пособиях, по геометрии используемых в школе данная тема имеет место.
Слайд 3О подобии
Одинаковые по форме, но различные по величине фигуры встречаются в
вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров.
Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V—IV вв. до н. э. трудами Гиппократа Хиосского, Ар хита Тарентского, Евдокса Книдского и др. Оно изложено в VI книге «Начал» Евклида, начинающиеся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны».
Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V—IV вв. до н. э. трудами Гиппократа Хиосского, Ар хита Тарентского, Евдокса Книдского и др. Оно изложено в VI книге «Начал» Евклида, начинающиеся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны».
Слайд 4ИЗ ИСТОРИИ ПОДОБИЯ
Идея отношения и Пропорции зародилась в глубокой древности. Об
этом свидетельствуют древнеегипетские храмы, детали гробницы Менеса и знаменитых пирамид в Гизе (III тысячелетие до н. э.), вавилонские зиккураты (ступенчатые культовые башни), персидские Дворцы, Индийские и другие Памятники древности, Многие обстоятельства. В том числе особенности архитектуры, требования Удобства, Эстетики, техники и экономичности при возведении зданий и сооружений, вызвали возникновение и развитие понятий отношения и пропорциональности отрезков, площадей и других величин.
Слайд 5Преобразование подобия.
Определение преобразования подобия одинаково и на плоскости, и
в пространстве. Преобразование фигуры в фигуру называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Это значит, что если произвольные точки А и В фигуры F при этом преобразовании переходят в точки А1 и В1 фигуры F1 , то А1В1 = kАВ, где k > 0.
Слайд 7Признаки подобия
Первый признак – по двум углам.
Второй признак – по двум
сторонам и углу между ними.
Третий признак – по трем сторонам.
Третий признак – по трем сторонам.
Слайд 8Первый признак
Если два угла одного треугольника соответственно равны двум углам другого
треугольника, то треугольники подобны.
Таким образом, если в треугольниках АВС и А1В1С1 выполнены равенства (А = А1) и (B = В1), то треугольник АВС подобен треугольнику А1В1С1. При решении задач этот признак работает наиболее часто. Так же нужно обратить внимание на то, что в этом признаке оперируют всего 2 элемента – а именно,
углы . В остальных двух признаках фигурируют три элемента.
Таким образом, если в треугольниках АВС и А1В1С1 выполнены равенства (А = А1) и (B = В1), то треугольник АВС подобен треугольнику А1В1С1. При решении задач этот признак работает наиболее часто. Так же нужно обратить внимание на то, что в этом признаке оперируют всего 2 элемента – а именно,
углы . В остальных двух признаках фигурируют три элемента.
Слайд 9Второй признак
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника,
а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Таким образом, если в треугольниках АВС и А1В1С1
выполнены равенства: и А = А1, то
треугольники АВС и А1В1С1 подобны.
Таким образом, если в треугольниках АВС и А1В1С1
выполнены равенства: и А = А1, то
треугольники АВС и А1В1С1 подобны.
Слайд 10Третий признак
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника,
то такие треугольники подобны.
Таким образом, если в треугольниках АВС и А1В1С1 выполнены равенства:
= = , то треугольники АВС
и А1В1С1 подобны.
Таким образом, если в треугольниках АВС и А1В1С1 выполнены равенства:
= = , то треугольники АВС
и А1В1С1 подобны.