Преподаватель математики и информатики Багрова Г.Г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Параллелепипед. Куб. (10-11 класс)
Содержание
- 1. Презентация по математике на тему Параллелепипед. Куб. (10-11 класс)
- 2. Основные вопросы:Виды параллелепипеда (прямой, прямоугольный). Элементы параллелепипеда:
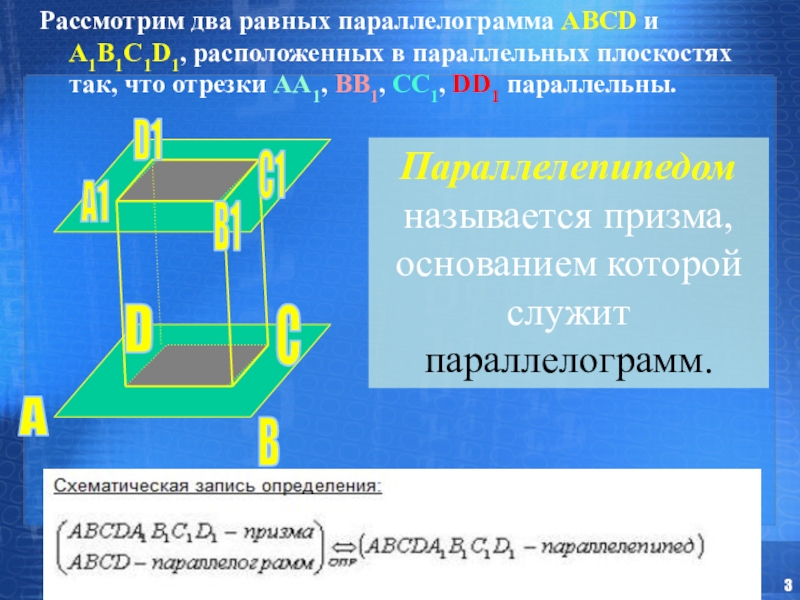
- 3. Рассмотрим два равных параллелограмма АВСD и А1В1С1D1,
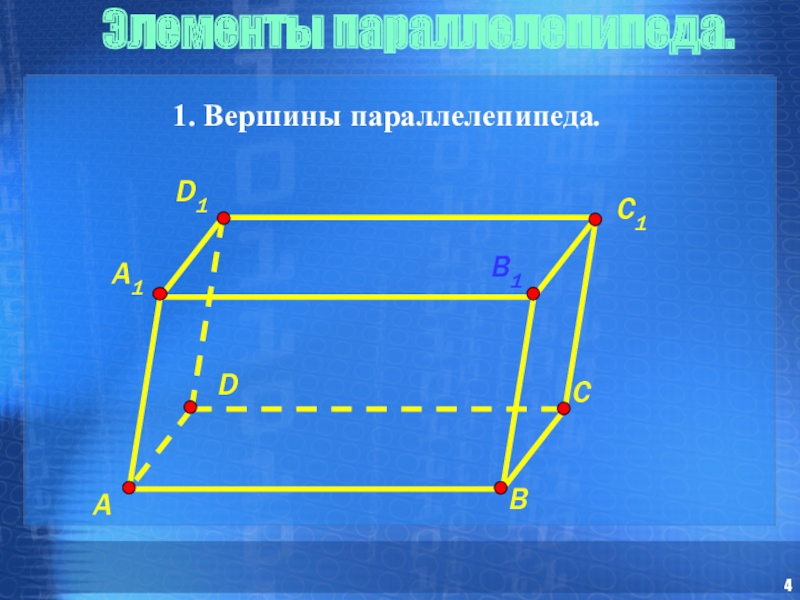
- 4. Элементы параллелепипеда. 1. Вершины параллелепипеда.
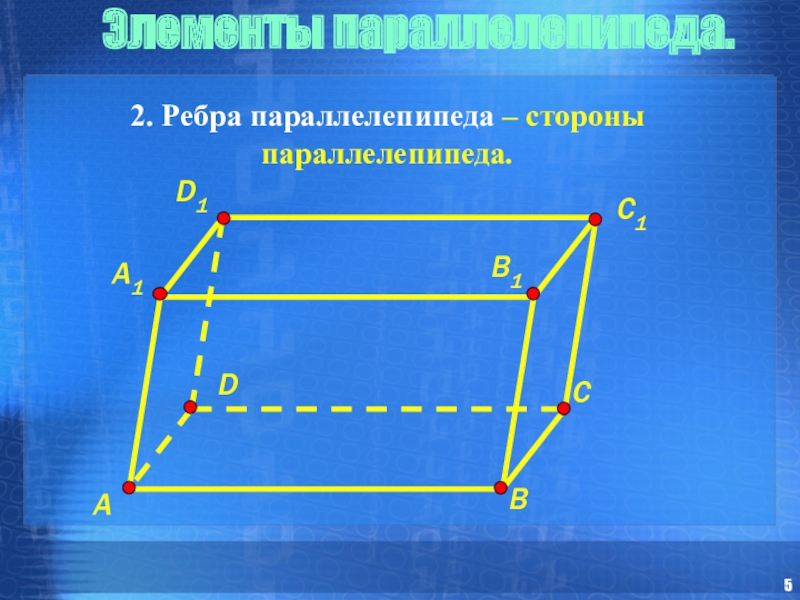
- 5. 2. Ребра параллелепипеда – стороны параллелепипеда.Элементы параллелепипеда.
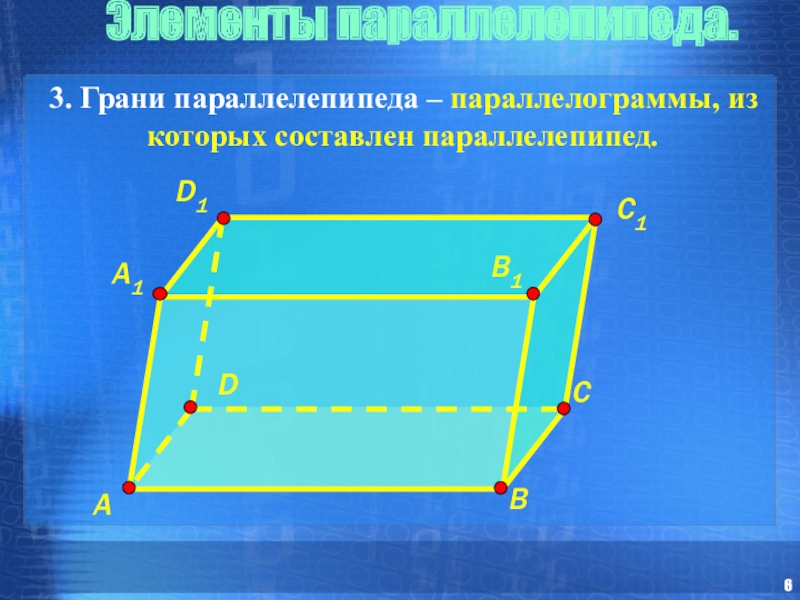
- 6. 3. Грани параллелепипеда – параллелограммы, из которых составлен параллелепипед. Элементы параллелепипеда.
- 7. имеют общее ребро4. Смежные граниЭлементы параллелепипеда.
- 8. не имеютобщих ребер5.ПротивоположныеграниЭлементы параллелепипеда.
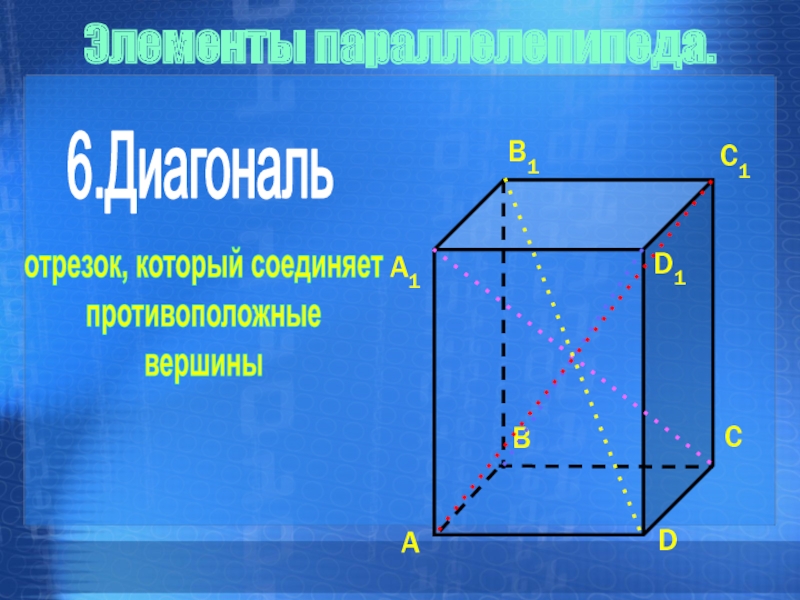
- 9. отрезок, который соединяет противоположныевершины6.ДиагональЭлементы параллелепипеда.
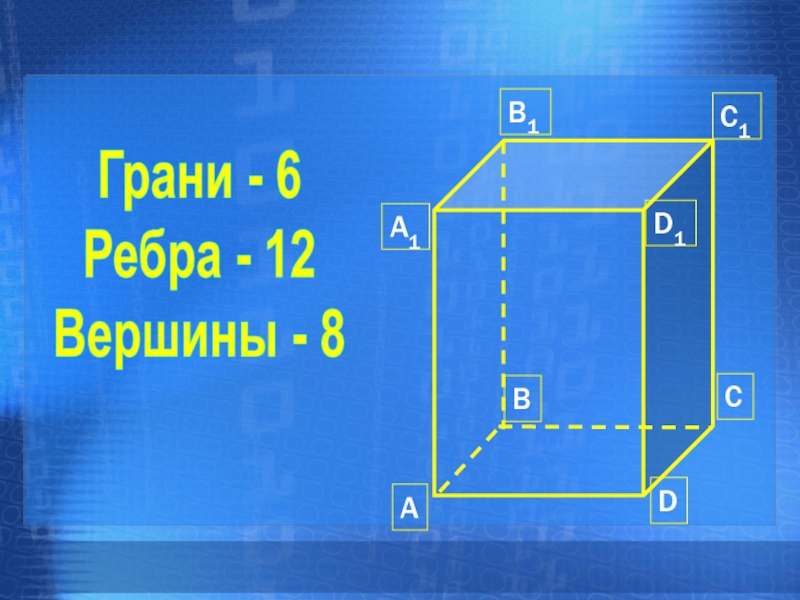
- 10. Грани - 6Ребра - 12Вершины - 8
- 11. Свойства параллелепипеда. Противоположные грани параллелепипеда равны и параллельны.
- 12. 2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополамСвойства параллелепипеда.
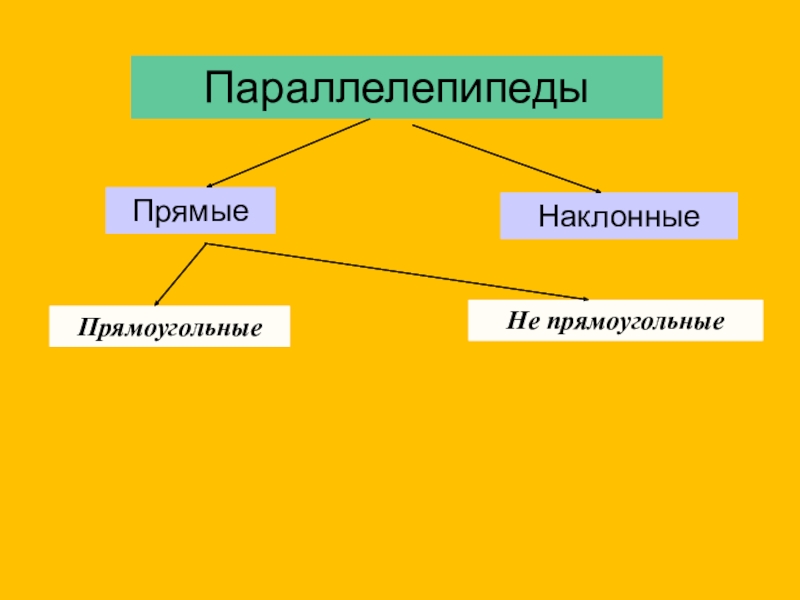
- 13. ПараллелепипедыПрямыеНаклонныеПрямоугольныеНе прямоугольные
- 14. Параллелепипед называется прямым, если его боковые рёбра перпендикулярны к основанию.У прямого параллелепипеда боковые грани – прямоугольники.
- 15. Параллелепипед называется прямоугольным, если его боковые рёбра
- 16. Наклонный параллелепипед Боковые грани и основания – параллелограммы
- 17. Куб – это прямоугольный параллелепипед, у которого
- 18. ТеоремаКвадрат длины любой диагонали прямоугольного параллелепипеда равняется сумме квадратов трех его измерений: d2 = a2 + b2 +c2.
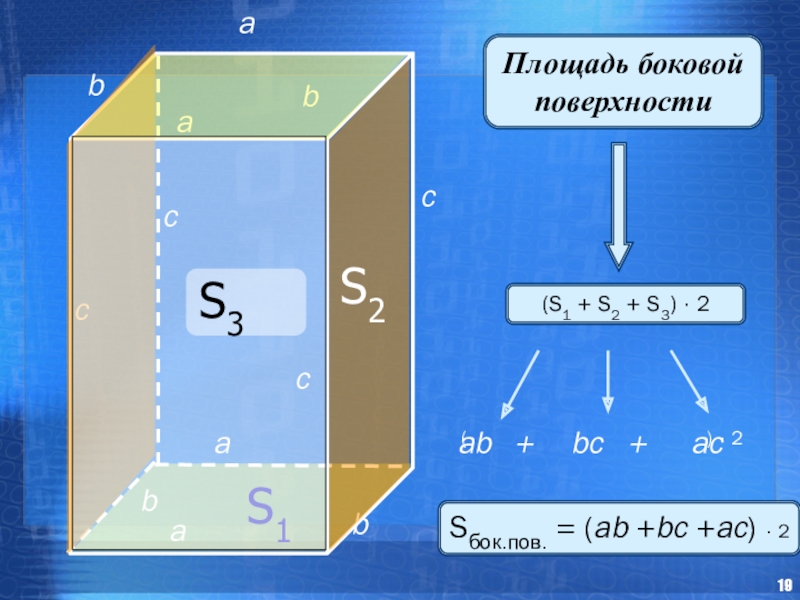
- 19. acbaaabbbcccS2S1(S1 + S2 + S3) · 2
- 20. ДОМАШНЕЕ ЗАДАНИЕ:Учебник Геометрия /Атанасян/ гл.1 §4( п.13)
Основные вопросы:Виды параллелепипеда (прямой, прямоугольный). Элементы параллелепипеда: вершины, грани, ребра, смежные грани, противоположные грани, противолежащие вершины, диагональ параллелепипеда, боковые грани, основания, боковые ребра.Свойства параллелепипеда.
Слайд 1Параллелепипед, его виды и
свойства
Урюпинский филиал ГБОУ СПО «Волгоградский медицинский
колледж»
Слайд 2Основные вопросы:
Виды параллелепипеда (прямой, прямоугольный). Элементы параллелепипеда: вершины, грани, ребра, смежные
грани, противоположные грани, противолежащие вершины, диагональ параллелепипеда, боковые грани, основания, боковые ребра.
Свойства параллелепипеда.
Свойства параллелепипеда.
Слайд 3Рассмотрим два равных параллелограмма АВСD и А1В1С1D1, расположенных в параллельных плоскостях
так, что отрезки АА1, ВВ1, СС1, DD1 параллельны.
Параллелепипедом называется призма, основанием которой служит параллелограмм.
Слайд 63. Грани параллелепипеда – параллелограммы, из которых составлен параллелепипед.
Элементы параллелепипеда.
Слайд 122. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой
пополам
Свойства параллелепипеда.
Слайд 14Параллелепипед называется прямым, если его боковые рёбра перпендикулярны к основанию.
У прямого
параллелепипеда боковые грани – прямоугольники.
Слайд 15Параллелепипед называется прямоугольным, если его боковые рёбра перпендикулярны к основанию, а
основанием является прямоугольник
У прямоугольного параллелепипеда все грани - прямоугольники.
Диагонали прямоугольного параллелепипеда равны.
Слайд 17Куб – это прямоугольный параллелепипед, у которого все ребра равны между
собой.
У куба все грани – равные квадраты
Три ребра, выходящие из одной вершины прямоугольного параллелепипеда называются его измерениями (длиной, шириной, высотой).
Слайд 18Теорема
Квадрат длины любой диагонали прямоугольного параллелепипеда равняется сумме квадратов трех его
измерений:
d2 = a2 + b2 +c2.
Слайд 19a
c
b
a
a
a
b
b
b
c
c
c
S2
S1
(S1 + S2 + S3) · 2
Площадь боковой поверхности
ab
bc
ac
+
+
(
) · 2
Sбок.пов. = (ab +bc +ac) · 2
Слайд 20ДОМАШНЕЕ ЗАДАНИЕ:
Учебник Геометрия /Атанасян/
гл.1 §4( п.13) ,
гл. 2 §3
(п.24) вопросы: 15 (стр.32)
№ 114, 115, 192, 195, 237, 298
№ 114, 115, 192, 195, 237, 298
