немного занимательным.
Б.Паскаль
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Медиана, биссектриса, высота (7 класс)
Содержание
- 1. Презентация по математике на тему Медиана, биссектриса, высота (7 класс)
- 2. Слайд 2
- 3. единственное числомножественное число,,высота
- 4. ,,,3биссектриса,,,,,,,,,,с
- 5. Биссектриса, медиана, высота.
- 6. Три девицы ,три сестрицы В треугольнике живут.
- 7. Медианой треугольника называют отрезок, соединяющий его
- 8. Биссектрисой треугольника называют отрезок
- 9. Высотой треугольника называют перпендикуляр
- 10. АВСРТКАК – медиана, ВК=КСВТ – медиана ,
- 11. Основное свойство медиан.
- 12. Медианы и площади. 1.
- 13. AF- биссектриса, ‹ CАF = ‹ FАBBD
- 14. Основное свойство.1. Биссектрисы внутренних углов треугольника
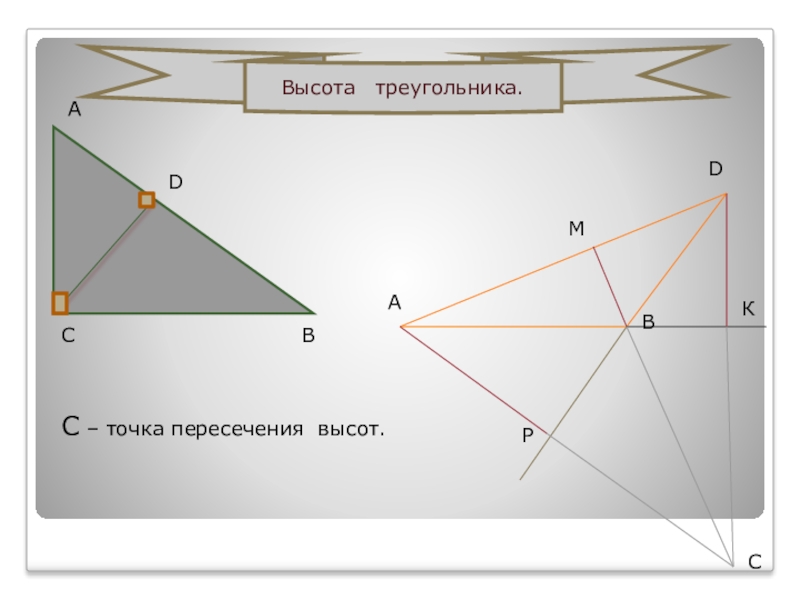
- 15. САВD Высота треугольника.САDВКМРС – точка пересечения высот.
, 3 a Тема нашего
Слайд 6Три девицы ,три сестрицы В треугольнике живут. Речь такую там ведут :
- Всех главнее высота!
Говорю вам неспроста .
Видят все как сторонам
Нужен перпендикуляр.
Тогда они, сменив
названья
Зовутся гордо -
основанья!
-Нет, - сказала медиана, -
Спорить я не перестану.
И на это есть причина:
Я треугольника вершину
Соединяю с серединой стороны
К тому же я делю всю площадь пополам!
В спор вступила биссектриса:
- Спорить не имеет смысла!
Если трое соберёмся, в точке
мы пересечемся.
Это точка не простая.
Середина золотая;
Если циркулем владеешь,
Окружность ты вписать
сумеешь!
Значит, всех я вас главнее!
В спор вмешался треугольник:
-Что вы, знает каждый школьник, что для меня вы все равны.
Будьте же всегда дружны!
Но вас предупреждаю я :
У каждой миссия своя!
Знает каждый школьник ,
Как меня построить.
К чему не проведут меня ,
Всем перпендикулярна я .
Отгадай, вопрос простой ,
Как зовусь я ? ( высотой ).
Вначале вы найти должны
Середину стороны.
Её соединить с вершиной,
и меня получишь ты.
Просто все и без обмана .
Как зовусь я ? ( медиана)
Слайд 7Медианой треугольника называют отрезок, соединяющий его сторону с серединой противоположной
стороны.
Для построения медианы треугольника необходимо выполнить следующие построения:
1. найти середину стороны;
2. соединить точку, являющуюся серединой стороны треугольника, с противоположной вершиной треугольника – это и будет медиана.
Слайд 8 Биссектрисой треугольника называют отрезок прямой , делящий угол
при вершине на две равные части.
Для построения биссектрисы треугольника необходимо выполнить следующие построения:
Построить биссектрису какого-либо угла треугольника ( а биссектриса угла – это луч, выходящий из вершины угла и делящий его на две равные части);
Найти точку пересечения биссектрисы угла с противоположной стороной;
Соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком – это и будет биссектриса.
Построить биссектрису какого-либо угла треугольника ( а биссектриса угла – это луч, выходящий из вершины угла и делящий его на две равные части);
Найти точку пересечения биссектрисы угла с противоположной стороной;
Соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком – это и будет биссектриса.
Слайд 9 Высотой треугольника называют перпендикуляр , опущенный из вершины
треугольника на противоположную сторону или её продолжение.
Для построения высоты треугольника необходимо выполнить следующие построения:
Провести прямую, содержащую одну из сторон треугольника ( в случае, если из вершины острого угла в тупоугольном треугольнике );
Из вершины, лежащей напротив проведенной прямой , опустить перпендикуляр к ней ( а перпендикуляр – это отрезок, проведенный из точки к прямой, составляющий с ней угол 90°) – это и будет высота.
Для построения высоты треугольника необходимо выполнить следующие построения:
Провести прямую, содержащую одну из сторон треугольника ( в случае, если из вершины острого угла в тупоугольном треугольнике );
Из вершины, лежащей напротив проведенной прямой , опустить перпендикуляр к ней ( а перпендикуляр – это отрезок, проведенный из точки к прямой, составляющий с ней угол 90°) – это и будет высота.
Слайд 10
А
В
С
Р
Т
К
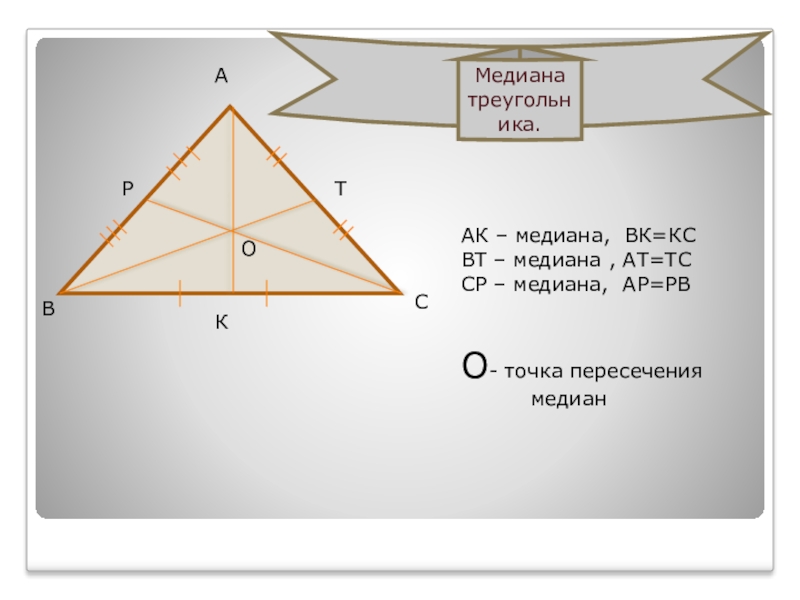
АК – медиана, ВК=КС
ВТ – медиана , АТ=ТС
СР – медиана, АР=РВ
О-
точка пересечения
медиан
медиан
О
Медиана треугольника.
Слайд 11Основное свойство медиан.
В любом
треугольнике медианы пересекаются в одной точке и делятся этой точкой в отношении 2 :1 , считая от вершины.
Точка пересечения медиан треугольника имеет физический смысл: она является его центром масс.
Точка пересечения медиан треугольника имеет физический смысл: она является его центром масс.
Слайд 12 Медианы и площади.
1. Медиана разбивает треугольник на
два равновеликих , то есть имеющих одинаковую площадь.
2. Три медианы разбивают треугольник на шесть равновеликих.
3. Отрезки, соединяющие точку пересечения медиан с вершинами треугольника , разбивают треугольник на три равновеликие части.
2. Три медианы разбивают треугольник на шесть равновеликих.
3. Отрезки, соединяющие точку пересечения медиан с вершинами треугольника , разбивают треугольник на три равновеликие части.
Слайд 13
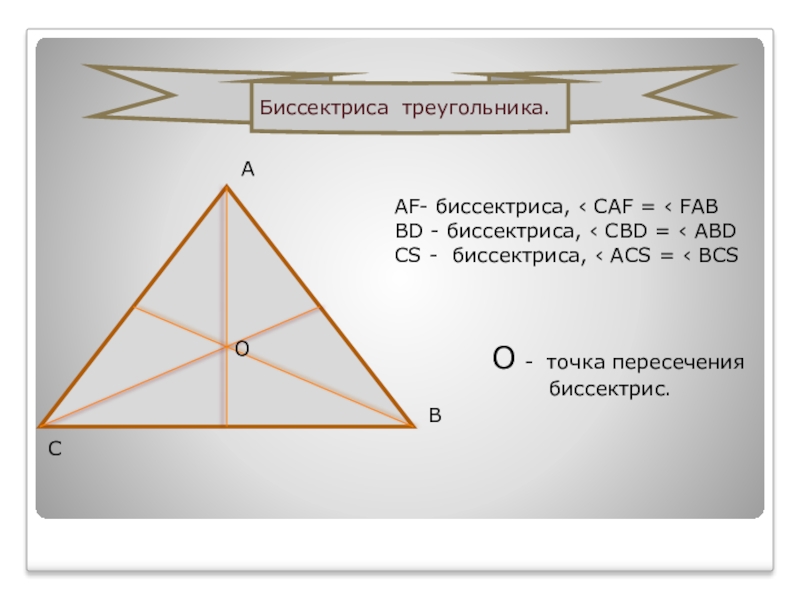
AF- биссектриса, ‹ CАF = ‹ FАB
BD - биссектриса, ‹ CBD
= ‹ АBD
CS - биссектриса, ‹ АCS = ‹ BCS
О - точка пересечения
биссектрис.
CS - биссектриса, ‹ АCS = ‹ BCS
О - точка пересечения
биссектрис.
A
B
C
О
Биссектриса треугольника.
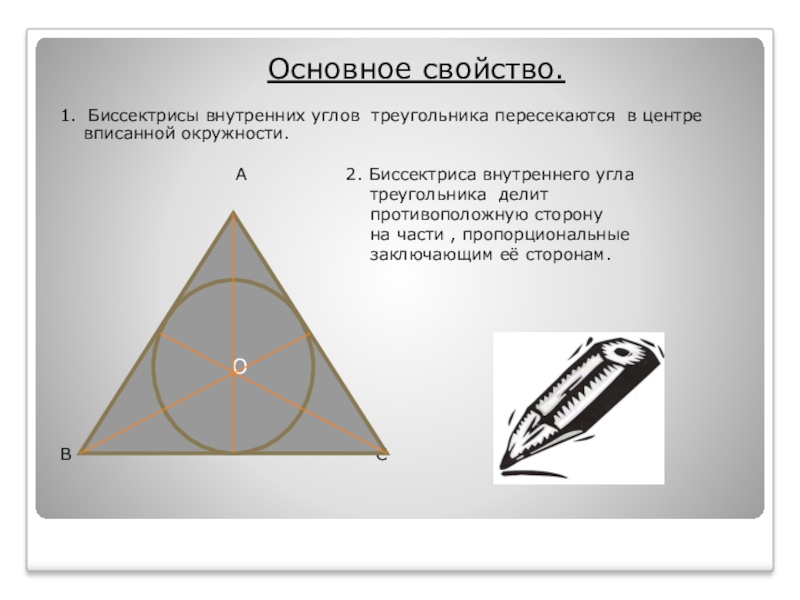
Слайд 14 Основное свойство.
1. Биссектрисы внутренних углов треугольника пересекаются в центре вписанной
окружности.
А 2. Биссектриса внутреннего угла
треугольника делит
противоположную сторону
на части , пропорциональные
заключающим её сторонам.
В С
А 2. Биссектриса внутреннего угла
треугольника делит
противоположную сторону
на части , пропорциональные
заключающим её сторонам.
В С
О