способностей и дает нам возможность правильно мыслить и рассуждать
Г. Галилей
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Формулы объемов тел
Содержание
- 1. Презентация по математике Формулы объемов тел
- 2. Папаллелепипед
- 3. параллелепипед
- 4. усеченный конус
- 5. Усеченный конус
- 6. усеченный конус
- 7. Цилиндр
- 8. Цилиндр
- 9. Цилиндр
- 10. четырехугольная призма
- 11. Четырёхугольная призма
- 12. Треугольная призма
- 13. Треугольная призма
- 14. Треугольная призма
- 15. Цель урока: изучить формулу призмы, выработать навыки решения задач с использованием формулы объема призмы
- 16. Объем это величина, которая показывает,сколько раз единица измеренияобъема укладывается в даннойфигуре.
- 17. Объем куба рассчитывается по формуле: V = a³Объем параллелепипеда рассчитывается по формуле:V = a∙b∙c
- 18. Задача. Вычислите объем куба, если его сторона
- 19. Определение 1.Многогранник, две грани которого - одноименные
- 20. ПризмаВсе призмы делятся на прямые и наклонные.
- 21. ОБЪЕМ ПРИЗМЫТеорема. Объем призмы равен произведению площади
- 22. Решение задач Задача 1. Дана правильная
- 23. Задача 2. Вычислите объем прямой призмы в
- 24. Объем призмы равен V=Sосн∙h, где Sосн -площадь основания, h-высота призмы
- 25. Домашнее заданиеВычислите объем прямой призмы в основании
Папаллелепипед
Слайд 1Формула объема призмы
Геометрия является самым могущественным средством для изощрения наших умственных
Слайд 15Цель урока:
изучить формулу призмы, выработать навыки решения задач с использованием
формулы объема призмы
Слайд 16Объем это
величина, которая показывает,
сколько раз единица измерения
объема укладывается в данной
фигуре.
Слайд 17Объем куба рассчитывается по формуле:
V = a³
Объем параллелепипеда рассчитывается по
формуле:
V = a∙b∙c
V = a∙b∙c
Слайд 18Задача. Вычислите объем куба, если его сторона равна 2 м.
Дано:
а=2 м
Найти:
V=?
Решение:
V
= a³
V = 2³ = 8 м³
Ответ: 8 м³
V = 2³ = 8 м³
Ответ: 8 м³
Слайд 19Определение 1.
Многогранник, две грани которого - одноименные многоугольники, лежащие в параллельных
плоскостях, а любые два ребра, не лежащие в этих плоскостях, параллельны, называется призмой.
Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело).
Многоугольники, лежащие в параллельных плоскостях, называют основаниями призмы, а остальные грани - боковыми гранями. Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания.
Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело).
Многоугольники, лежащие в параллельных плоскостях, называют основаниями призмы, а остальные грани - боковыми гранями. Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания.
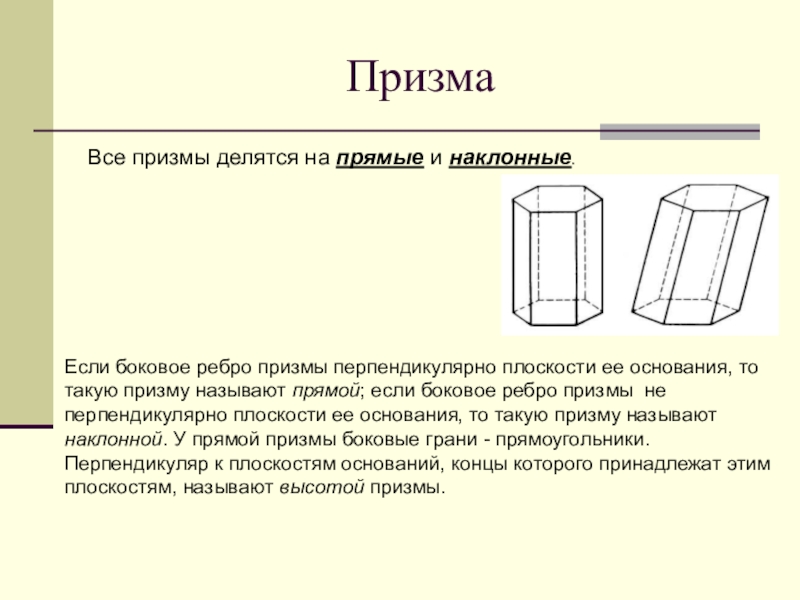
Слайд 20Призма
Все призмы делятся на прямые и наклонные.
Если боковое ребро призмы перпендикулярно
плоскости ее основания, то такую призму называют прямой; если боковое ребро призмы не перпендикулярно плоскости ее основания, то такую призму называют наклонной. У прямой призмы боковые грани - прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы.
Слайд 21ОБЪЕМ ПРИЗМЫ
Теорема.
Объем призмы равен произведению площади основания на высоту.
Следствие.
Объем
прямой призмы равен произведению площади основания на длину бокового ребра:V=Sосн∙b (Sосн -площадь основания, b- длина бокового ребра)
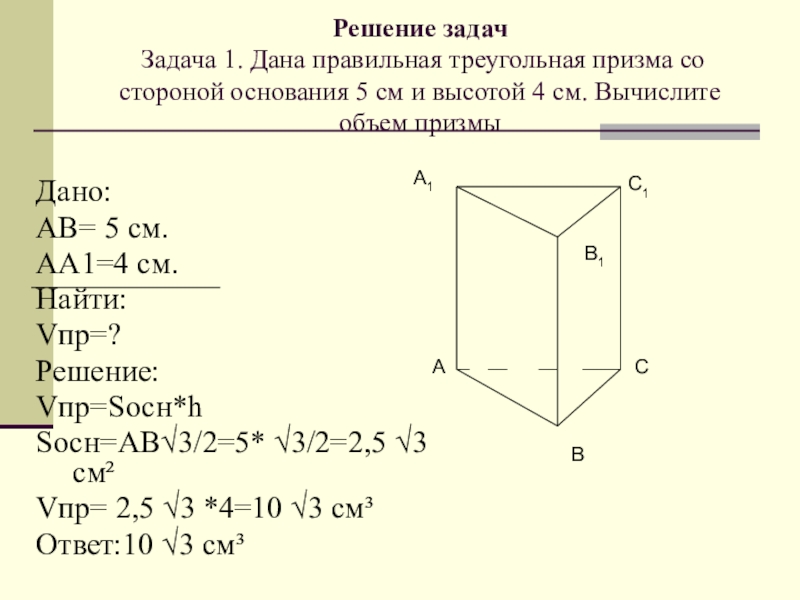
Слайд 22Решение задач Задача 1. Дана правильная треугольная призма со стороной основания
5 см и высотой 4 см. Вычислите объем призмы
Дано:
АB= 5 см.
AA1=4 см.
Найти:
Vпр=?
Решение:
Vпр=Sосн*h
Sосн=AB√3/2=5* √3/2=2,5 √3 см²
Vпр= 2,5 √3 *4=10 √3 см³
Ответ:10 √3 см³
В
А
С
А1
С1
В1
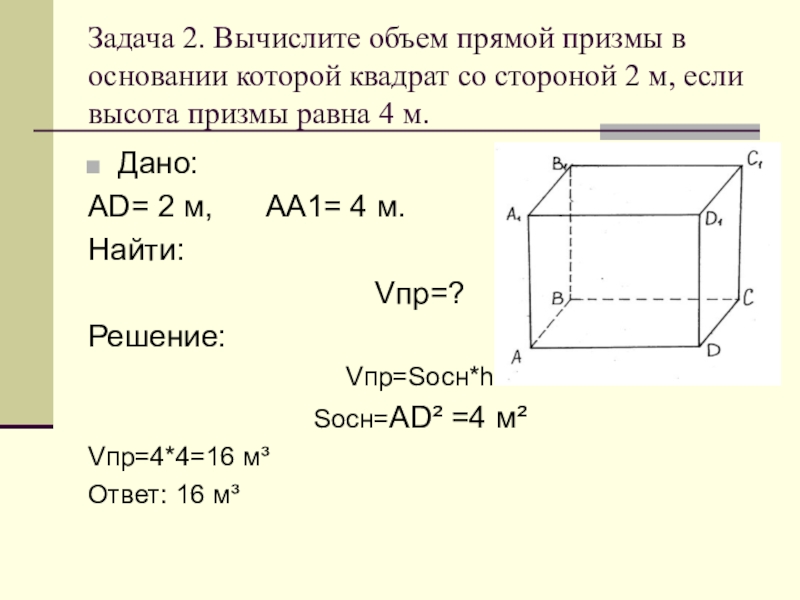
Слайд 23Задача 2. Вычислите объем прямой призмы в основании которой квадрат со
стороной 2 м, если высота призмы равна 4 м.
Дано:
АD= 2 м, AA1= 4 м.
Найти:
Vпр=?
Решение:
Vпр=Sосн*h
Sосн=AD² =4 м²
Vпр=4*4=16 м³
Ответ: 16 м³
Слайд 25Домашнее задание
Вычислите объем прямой призмы в основании которой лежит прямоугольник со
сторонами 5 и 3 см, если боковое ребро призмы равно 10 см.
В прямоугольной призме площадь основания равна 12 см², а ее высота в 2 раза больше меньшей стороны основания. Вычислите объем призмы, если одна из сторон основания равна 4 см.
В прямоугольной призме площадь основания равна 12 см², а ее высота в 2 раза больше меньшей стороны основания. Вычислите объем призмы, если одна из сторон основания равна 4 см.