- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии:Площади многоугольников
Содержание
- 1. Презентация по геометрии:Площади многоугольников
- 2. СодержаниеВведение1. Вычисление площадей в древности2. Площадь многоугольников2.1.
- 3. Введение«Большой Энциклопедический словарь» МНОГОУГОЛЬНИК — геометрическая фигура,
- 4. Введение Измерение площадей считают одним из самых древних
- 5. 1. Вычисление площадей в древностиЕще 4-5 тысяч
- 6. 1. Вычисление площадей в древности
- 7. 1. Вычисление площадей в древностиДля вычисления площади
- 8. 1. Вычисление площадей в древностиДля определения площади
- 9. 2. Площадь многоугольников «Площадь многоугольника – это величина
- 10. 2.1 Площадь прямоугольника Теорема. Площадь прямоугольника
- 11. 2.2 Площадь параллелограмма Теорема.
- 12. 2.3 Площадь треугольника Теорема. Площадь
- 13. 3. Способы нахождения площади многоугольников
- 14. 3. Способы нахождения площади многоугольников
- 15. 3. Способы нахождения площади многоугольников
- 16. 4. Задачи по нахождению площади многоугольника Задача 1
- 17. 4. Задачи по нахождению площади многоугольника
- 18. 4. Задачи по нахождению площади многоугольника
- 19. 4. Задачи по нахождению площади многоугольника
- 20. 4. Задачи по нахождению площади многоугольника
- 21. 4. Задачи по нахождению площади многоугольника
- 22. 4. Задачи по нахождению площади многоугольника
- 23. 4. Задачи по нахождению площади многоугольника
- 24. ЗаключениеОсновная сложность изучения нахождения площади многоугольников состоит
- 25. Список используемой литературыБольшой Энциклопедический словарь Научно-технический энциклопедический
Слайд 2Содержание
Введение
1. Вычисление площадей в древности
2. Площадь многоугольников
2.1. Площадь прямоугольника
2.2. Площадь параллелограмма
2.3.
3. Способы нахождения площади многоугольников
4. Задачи по нахождению площади многоугольника
Заключение
Список используемой литературы
Слайд 3Введение
«Большой Энциклопедический словарь»
МНОГОУГОЛЬНИК — геометрическая фигура, ограниченная замкнутой ломаной линией,
«Научно-технический энциклопедический словарь»
МНОГОУГОЛЬНИК — геометрическая фигура с тремя или более сторонами, пересекающимися в трех или более точках (вершинах). Они называются в соответствии с числом сторон или вершин: ТРЕУГОЛЬНИК (трехсторонний); ЧЕТЫРЕХУГОЛЬНИК…
«Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова.»
МНОГОУГОЛЬНИК — геометрическая фигура, ограниченная замкнутой ломаной линией.
«Большая советская энциклопедия»
МНОГОУГОЛЬНИК — замкнутая ломаная линия, которая получается, если взять n любых точек A1, A2, ..., An и соединить прямолинейным отрезком каждую из них с последующей, а последнюю с первой.
Слайд 4Введение
Измерение площадей считают одним из самых древних разделов геометрии. В частности,
Одним из поздних греческих математиков - энциклопедистов, труды которого имели главным образом прикладной характер, был Герон Александрийский, живший в 1 в. н. э.
Одна из книг Герона была названа им «Метрика» и является своего рода сборником формул и соответствующих задач. Она содержит примеры на вычисление площадей квадратов, прямоугольников и треугольников.
Слайд 51. Вычисление площадей в древности
Еще 4-5 тысяч лет назад вавилоняне умели
Древние египтяне 4000 лет назад пользовались почти теми же приемами, что и мы. Для измерения площади прямоугольника, треугольника и трапеции: основание треугольника делилось пополам и умножалось на высоту.
Слайд 61. Вычисление площадей в древности
В «Метрике» Герон излагает
где a,b,c ‑ стороны, p‑ полупериметр треугольника.
Эта формула носит название «формулы Герона».
На самом деле она была установлена еще в 3 в. до н. э. величайшим математиком древности Архимедом.
Практические правила Герона для вычисления площадей применялись греческими, римскими и средневековыми землемерами и техниками.
Слайд 71. Вычисление площадей в древности
Для вычисления площади четырехугольника со сторонами a,b,c,d
т.е. умножались полусуммы противоположных сторон.
Эта формула явно неверна для любого четырехугольника, из нее вытекает, в частности, что площади всех ромбов одинаковы. Между тем, очевидно, что у таких ромбов площади зависят от величины углов при вершинах. Данная формула верна только для прямоугольника. С ее помощью можно вычислить приближенно площадь четырехугольников, у которых углы близки к прямым.
Слайд 81. Вычисление площадей в древности
Для определения площади равнобедренного треугольника, в котором
Совершаемая при этом ошибка тем меньше, чем меньше разность между стороной AB и высотой AD треугольника, иными словами, чем ближе вершина B (и C) к основанию D высоты из A. Вот почему приближенная формула применима лишь для треугольников с сравнительно малым углом при вершине.
Слайд 92. Площадь многоугольников
«Площадь многоугольника – это величина той части плоскости, которую
За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков.» (Учебник геометрии 7-9класс)
Площадь многоугольника — положительная величина, численное значение которой обладает такими свойствами:
1. Равные многоугольники имеют равные площади
2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
3. За единицу измерения площади принимается площадь квадрата со стороной, равной 1 единице длины.
Для нахождения площади многоугольников необходимо знать формулы нахождения простейших многоугольников (треугольник, трапеция, прямоугольник, параллелограмм).
Слайд 102.1 Площадь прямоугольника
Теорема. Площадь прямоугольника равна
произведению его смежных
Доказательство:
Пусть нам дан прямоугольник
со сторонами a, b и площадью S.
Достроим прямоугольник до квадрата
со стороной a + b.
Площадь этого квадрата (a+b)(a+b).
С другой стороны, этот квадрат составлен из данного прямоугольника с площадью S, равного ему прямоугольника с площадью S и двух квадратов с площадями aa и bb. Из чего имеем:
(a+b)(a+b)=S+S+aa+bb
aa+2ab+bb=2S+aa+bb
Отсюда получаем: что S=ab
Теорема доказана.
Слайд 112.2 Площадь параллелограмма
Теорема. Площадь параллелограмма
равна произведению
Доказательство:
Рассмотрим параллелограмм АВСD с площадью S.
Примем сторону AD за основание и проведём высоты ВН и СК.
Докажем, что S=AD·ВН.
Докажем сначала, что площадь прямоугольника НВСК также равна S. Трапеция АВСК составлена из параллелограмма АВСD и треугольника DCK.
С другой стороны, она составлена из прямоугольника НВСК и треугольника АВН. Но прямоугольные треугольники DCK и АВН равны по гипотенузе и острому углу (их гипотенузы АВ и СD равны как противоположные стороны параллелограмма, а ∠ВАН = ∠CDK как соответственные углы при пересечении параллельных прямых АВ и СD секущей AD), поэтому их площади равны.
Следовательно, площади параллелограмма ABCD и прямоугольника НВСК также равны, т.е. площадь прямоугольника НВСК равна S. По теореме о площади прямоугольника S=BC·BH, а так как ВС=AD, то S=AD·BH.
Слайд 122.3 Площадь треугольника
Теорема. Площадь треугольника равна
половине произведения
проведённую к ней высоту:
Доказательство:
Данный треугольник АВС достроим до параллелограмма ABDC. Треугольники ABC и DCB равны по трём сторонам, поэтому их площади равны.
Значит площадь треугольника АВС равна половине площади параллелограмма ABDC, т. е.
Слайд 133. Способы нахождения площади многоугольников
Существует несколько способов нахождения
Один из них - приём «разрезания и складывания».
Суть: Если многоугольник разрезан на несколько многоугольников, то сумма их площадей равна площади исходного многоугольника. Фигуры надо разбивать на такие многоугольники, площадь которых мы умеем находить (треугольник, трапеция, прямоугольник, параллелограмм).
Слайд 143. Способы нахождения площади многоугольников
Вариант 1:
а) многоугольник
б) находим площадь каждой фигуры, на которые разбили многоугольник;
в) находим сумму площадей фигур;
г) полученная сумма и является площадью данного многоугольника.
Слайд 153. Способы нахождения площади многоугольников
Вариант 2:
а) многоугольник
б) составляется фигура, площадь которой умеем находить;
в) площадь полученной фигуры и является площадью исходного многоугольника.
Слайд 164. Задачи по нахождению площади многоугольника
Задача 1
С
и складывания» доказать, что площадь
трапеции равна произведению одной из
боковых сторон на перпендикуляр,
опущенный на неё из середины другой боковой стороны.
Решение:
Пусть АВСD – данная трапеция (AD || BC), К – середина стороны CD, КН – перпендикуляр, опущенный из точки К на прямую АВ. Проведём через точку К прямую, параллельную прямой АВ. Пусть М и Р – точки её пересечения с прямой ВС и AD.
Параллелограмм АВМР равновелик данной трапеции, т.к. АВСD = АВСКР + РКD= АВСКР + КСМ = АВМР, т.к. ΔРКD = ΔМКС (по стороне и двум прилежащим к ней углам): СК = КD (по условию), ∠РКD =∠МКС (как вертикальные).
Слайд 174. Задачи по нахождению площади многоугольника
∠КСМ = ∠
накрест лежащие углы при параллельных
прямых АD и ВМ), т.е. трапеция и
параллелограмм составлены из
одинаковых частей.
Поскольку площадь параллелограмма
равна произведению его основания АВ
на высоту КН, то
, (по построению),
(по доказанному), поэтому
, следовательно,
Слайд 184. Задачи по нахождению площади многоугольника
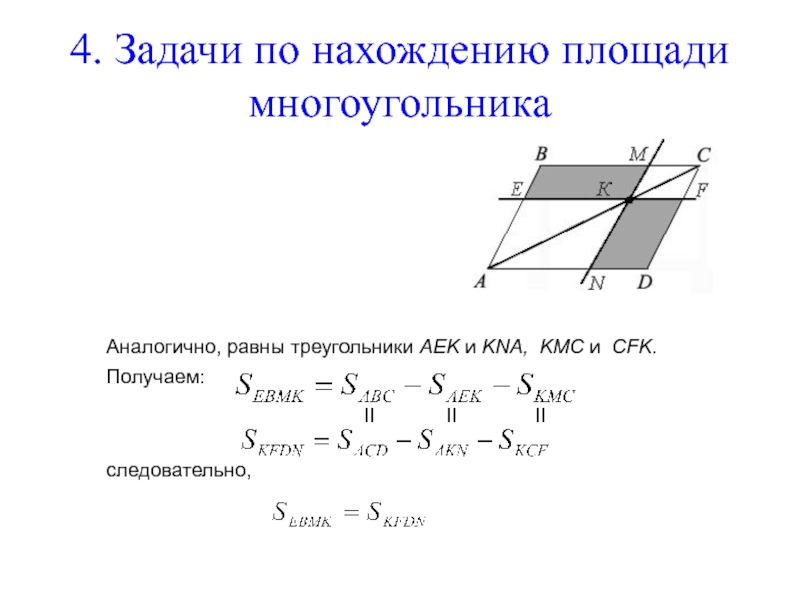
Задача
Через точку К, взятую на диагонали АС
параллелограмма ABCD, проведены
прямые, параллельные его сторонам.
Данный параллелограмм делится ими
на четыре параллелограмма. Два из
них пересекаются диагональю АС.
Доказать: два другие параллелограмма имеют равные площади.
Доказательство:
Диагональ АС делит параллелограмм на два равных треугольника ABC и АCD. Треугольники ABC и АCD равны по трем сторонам (сторона АС - общая, АВ=CD, AD=BC (по свойству параллелограмма)), поэтому их площади равны.
Слайд 194. Задачи по нахождению площади многоугольника
Аналогично,
Получаем:
следовательно,
II II II
Слайд 204. Задачи по нахождению площади многоугольника
Задача 3.
правильного восьмиугольника равна
произведению наибольшей и
наименьшей из его диагоналей.
Доказательство:
Достроим ΔАВС до прямоугольника АРОС.
ΔАВК = ΔАРВ (по стороне и двум прилежащим
к ней углам, т.к. ∠ ВАС = ∠ РВА (как накрест
лежащие углы при параллельных прямых РО и АС),
∠ВАР =∠АВК (как накрест лежащие углы при
параллельных прямых ВК и РА), сторона АВ – общая.
Достроим шестиугольник АВСМRL до прямоугольника FPOG.
Слайд 214. Задачи по нахождению площади многоугольника
Исходный восьмиугольник разделён
4 прямоугольника и 8 треугольников,
также, как и прямоугольник FPOG,
4 прямоугольника и 4 треугольника
у них общие, и все треугольники (в том числе и
по 4 оставшихся у каждой фигуры), на которые
разделены данные фигуры, равны
(т.к. ΔАВК= ΔАРВ по доказанному,
а исходный восьмиугольник – правильный).
Следовательно, исходный восьмиугольник равен прямоугольнику FPOG. Площадь прямоугольника равна произведению длины на ширину, а т.к. длина равна большей диагонали, ширина равна меньшей диагонали, то площадь правильного восьмиугольника равна произведению наибольшей и наименьшей диагоналей.
Слайд 224. Задачи по нахождению площади многоугольника
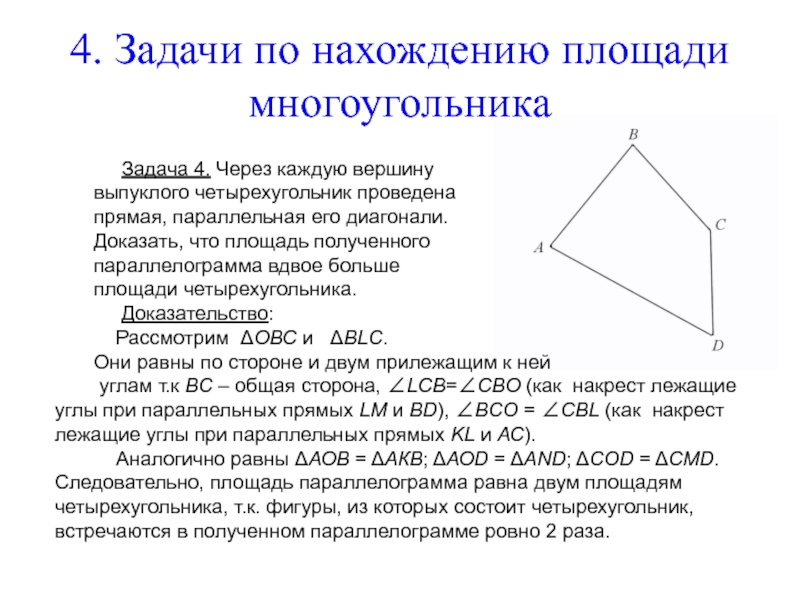
Задача 4. Через
выпуклого четырехугольник проведена
прямая, параллельная его диагонали.
Доказать, что площадь полученного
параллелограмма вдвое больше
площади четырехугольника.
Доказательство:
Рассмотрим ΔОВС и ΔBLC.
Они равны по стороне и двум прилежащим к ней
углам т.к ВС – общая сторона, ∠LCB=∠CBO (как накрест лежащие углы при параллельных прямых LM и BD), ∠BCO = ∠CBL (как накрест лежащие углы при параллельных прямых KL и АС).
Аналогично равны ΔАОВ = ΔАКВ; ΔАОD = ΔАND; ΔCOD = ΔCMD. Следовательно, площадь параллелограмма равна двум площадям четырехугольника, т.к. фигуры, из которых состоит четырехугольник, встречаются в полученном параллелограмме ровно 2 раза.
Слайд 234. Задачи по нахождению площади многоугольника
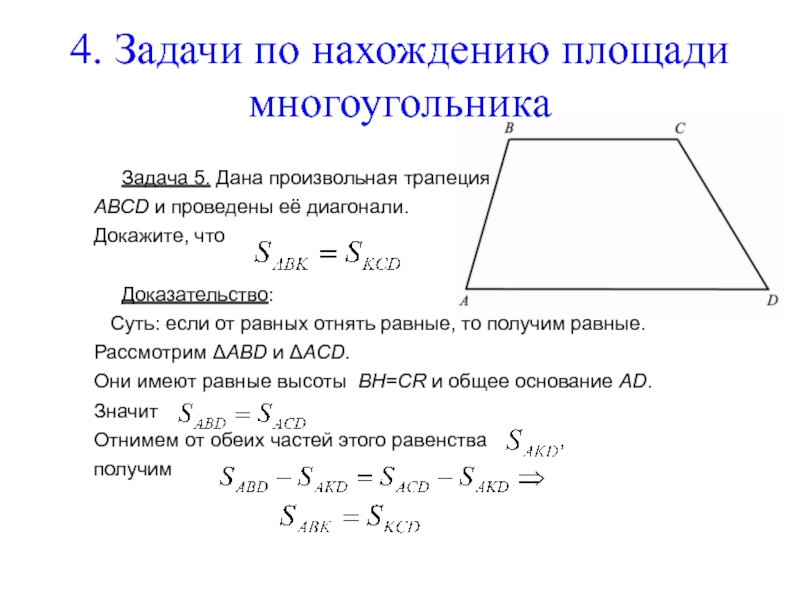
Задача 5. Дана
АВСD и проведены её диагонали.
Докажите, что
Доказательство:
Суть: если от равных отнять равные, то получим равные.
Рассмотрим ΔАВD и ΔACD.
Они имеют равные высоты BH=CR и общее основание АD.
Значит
Отнимем от обеих частей этого равенства ,
получим
Слайд 24Заключение
Основная сложность изучения нахождения площади многоугольников состоит в том, что не
Слайд 25Список используемой литературы
Большой Энциклопедический словарь
Научно-технический энциклопедический словарь
С.М.Шведов Толковый
Большая советская энциклопедия
Л.С.Атанасян, В.Ф.Бутузов Геометрия-учебник 7-9 класс- Москва, Просвещение, 2014.
П.Р.Кантор, Ж.М.Раббот Площади многоугольников «Квант» 1972.