- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Тетраэдр и параллелепипед
Содержание
- 1. Презентация по геометрии Тетраэдр и параллелепипед
- 2. Задача 1 Как при помощи шести
- 3. Задача. Как при помощи шести спичек
- 4. Тетраэдр
- 5. SПонятие тетраэдраАВСТетраэдр – (греч. tetréedro, от tetra, в сложных словах четыре и hedra – основание, грань)
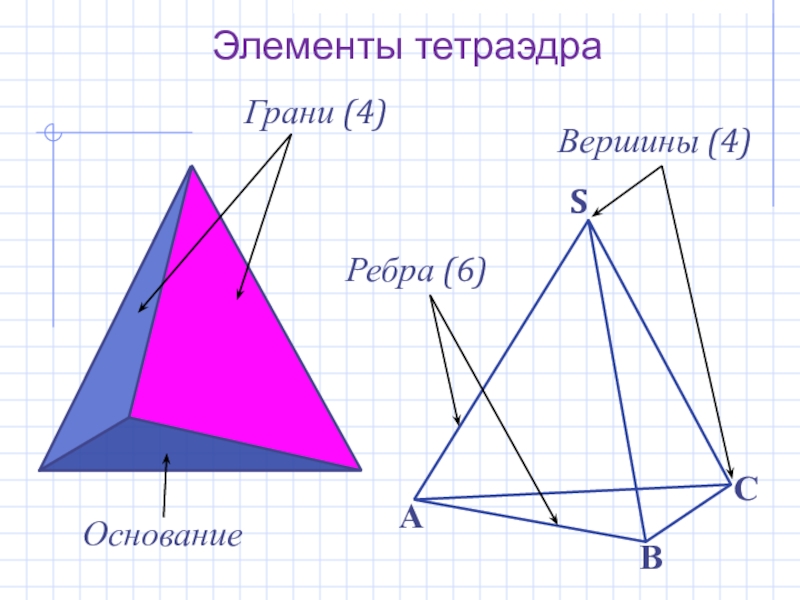
- 6. Элементы тетраэдраГрани (4)Ребра (6)Вершины (4)Основание
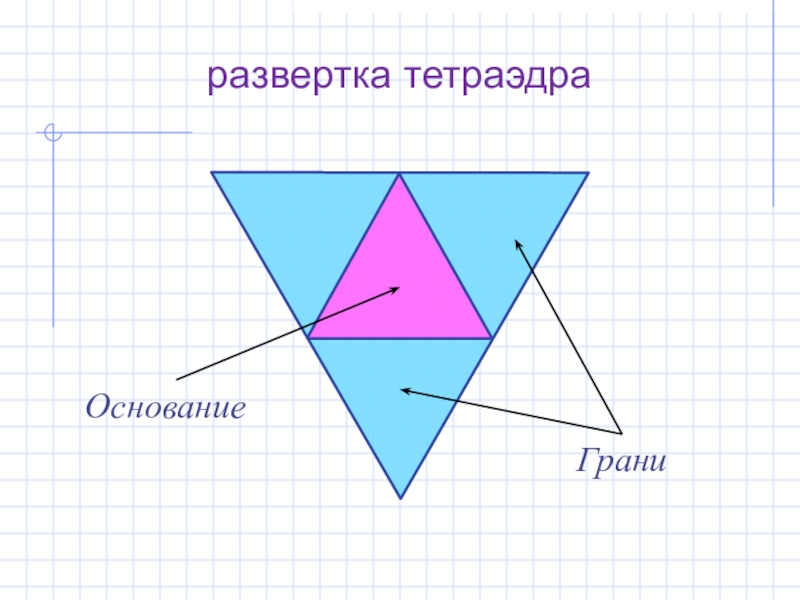
- 7. развертка тетраэдраГраниОснование
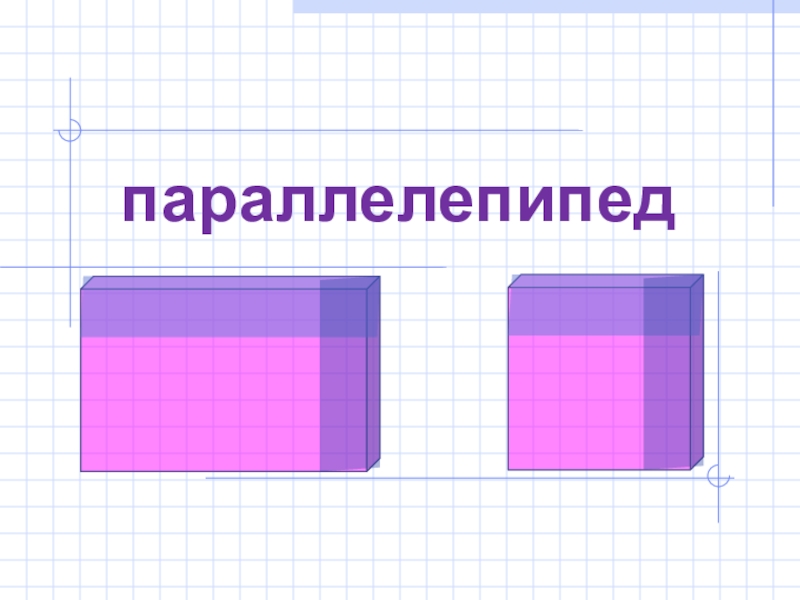
- 8. параллелепипед
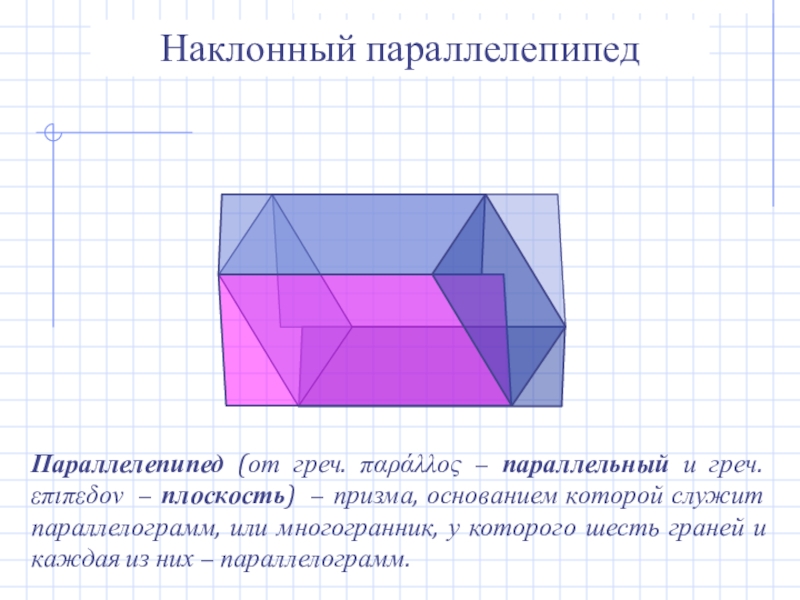
- 9. Наклонный параллелепипедПараллелепипед (от греч. παράλλος − параллельный
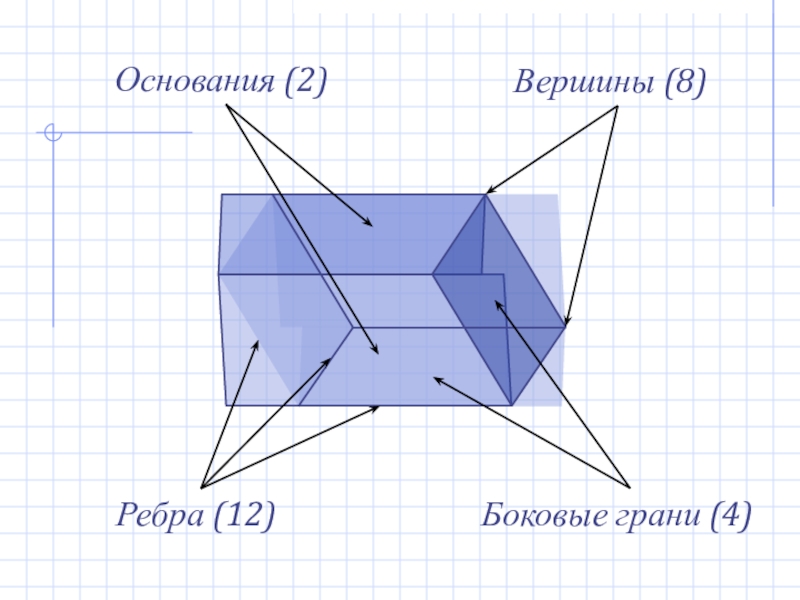
- 10. Ребра (12)Боковые грани (4)Вершины (8)Основания (2)
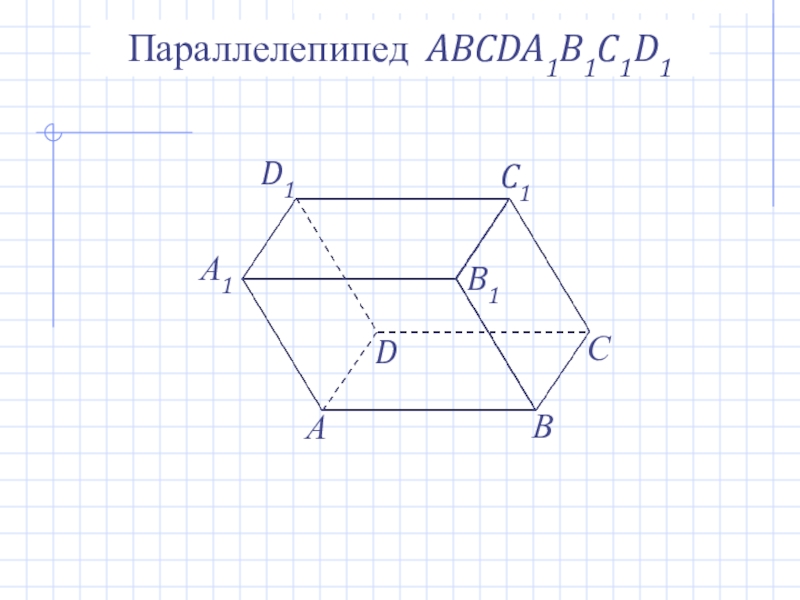
- 11. Параллелепипед ABCDA1B1C1D1
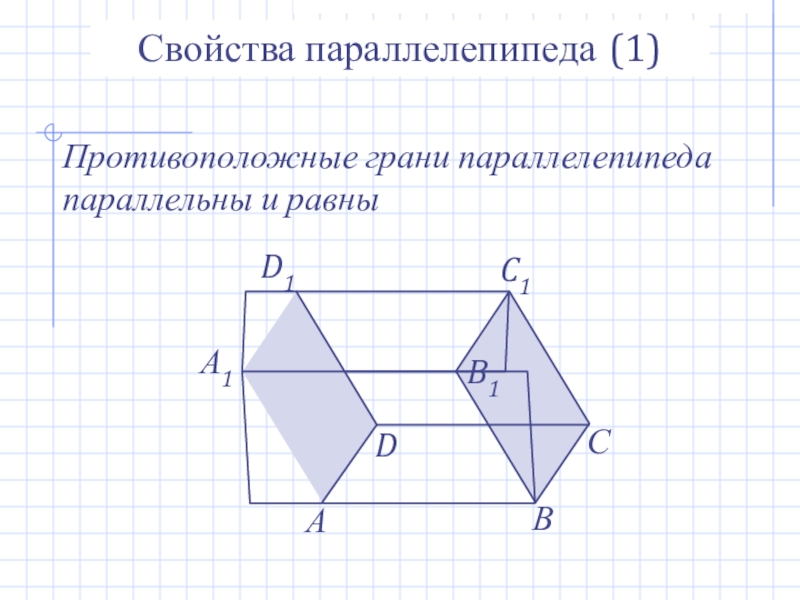
- 12. АВСА1DD1B1C1Свойства параллелепипеда (1)Противоположные грани параллелепипеда параллельны и равны
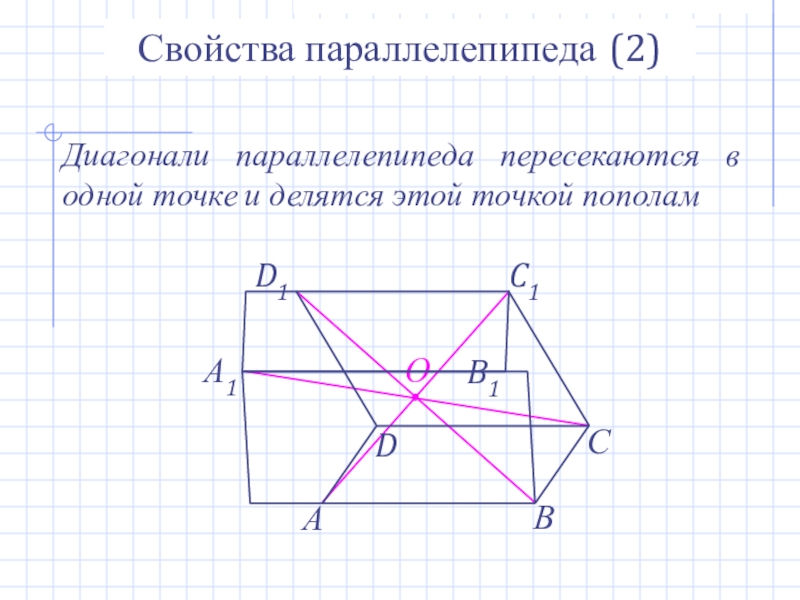
- 13. ОСвойства параллелепипеда (2)Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам
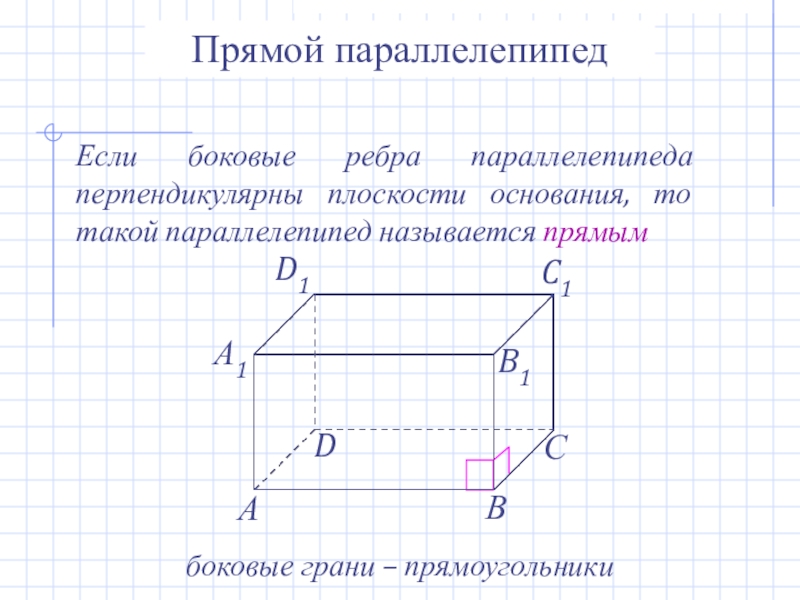
- 14. Прямой параллелепипедЕсли боковые ребра параллелепипеда перпендикулярны плоскости
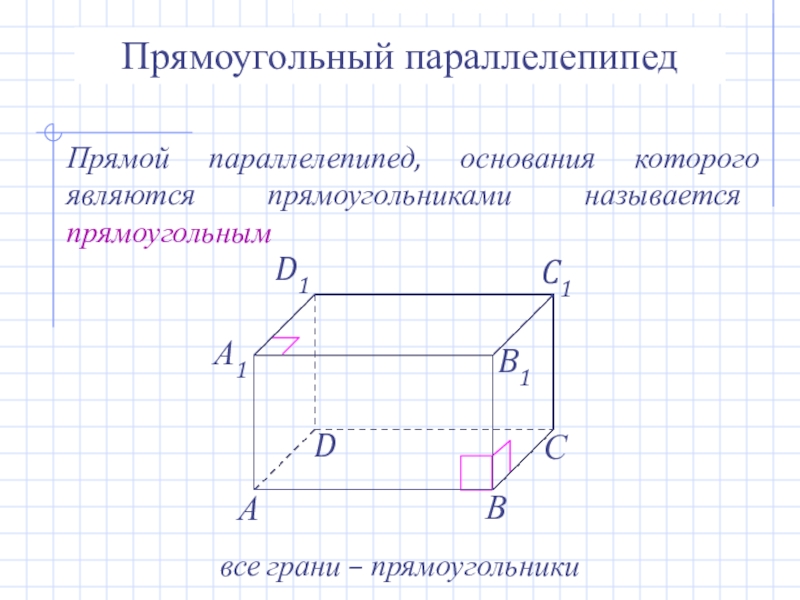
- 15. Прямоугольный параллелепипедПрямой параллелепипед, основания которого являются прямоугольниками называется прямоугольнымвсе грани – прямоугольники
- 16. Свойства прямоугольного параллелепипеда1° В прямоугольном параллелепипеде все
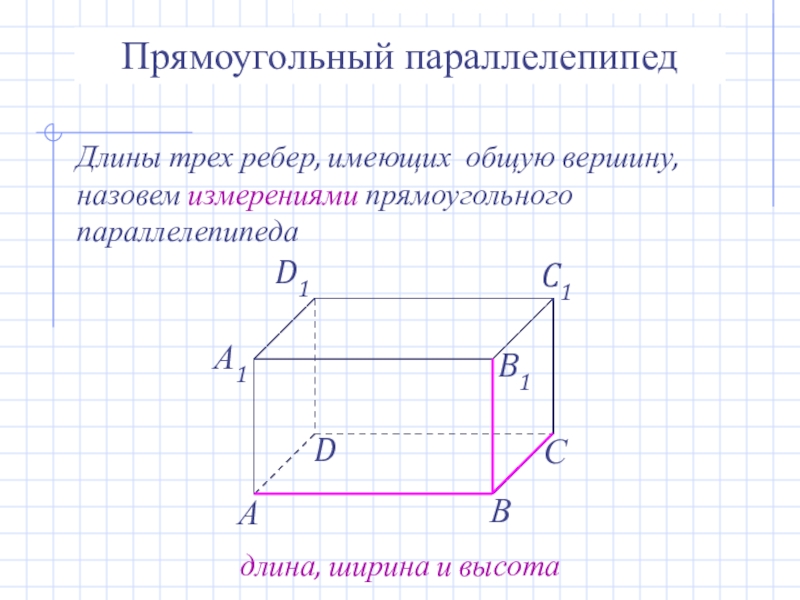
- 17. Прямоугольный параллелепипедДлины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипедадлина, ширина и высота
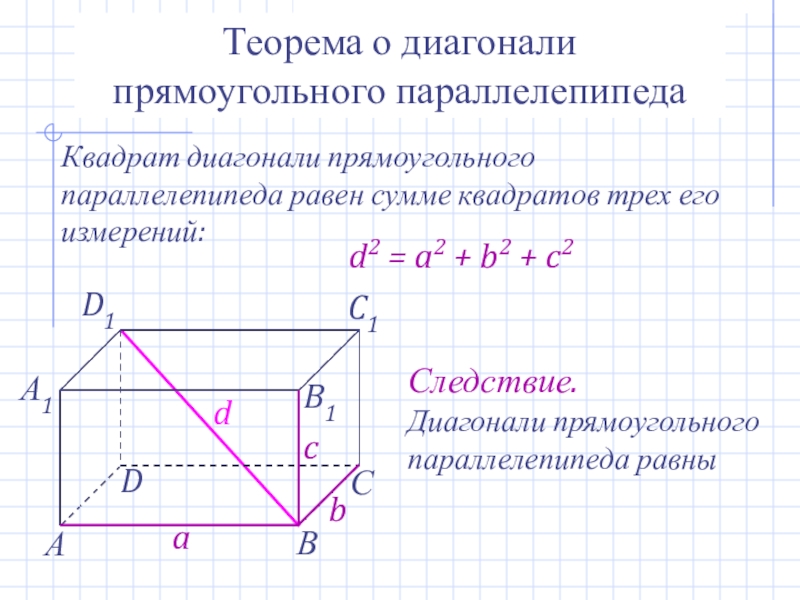
- 18. Теорема о диагонали прямоугольного параллелепипедаКвадрат диагонали прямоугольного
- 19. Куб Прямоугольный параллелепипед, все грани которого –
Задача 1 Как при помощи шести спичек сложить четыре одинаковых треугольника? Автор: Семёнова Елена ЮрьевнаМОУ СОШ №5 – «Школа здоровья и развития» г. Радужный
Слайд 2Задача 1 Как при помощи шести спичек сложить четыре одинаковых треугольника?
Автор: Семёнова Елена Юрьевна
МОУ СОШ №5 – «Школа здоровья и развития» г. Радужный
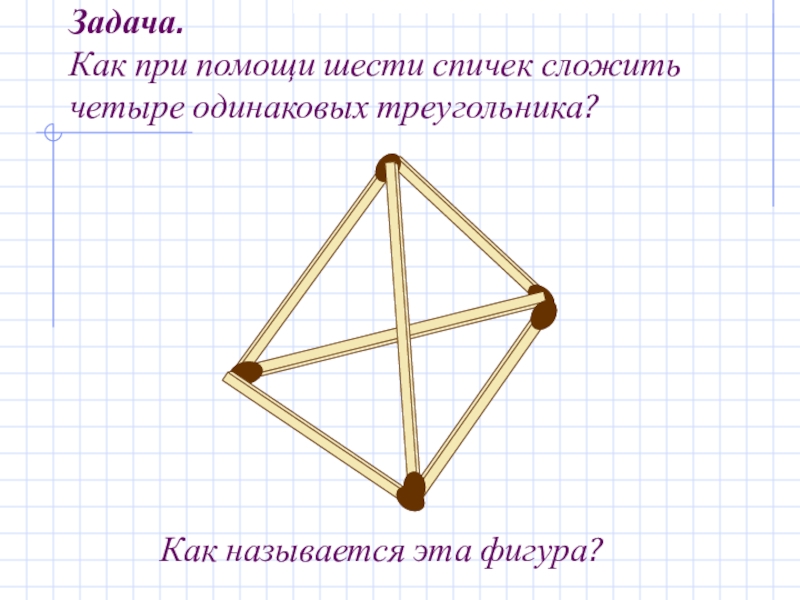
Слайд 3Задача.
Как при помощи шести спичек сложить
четыре одинаковых треугольника?
Как
называется эта фигура?
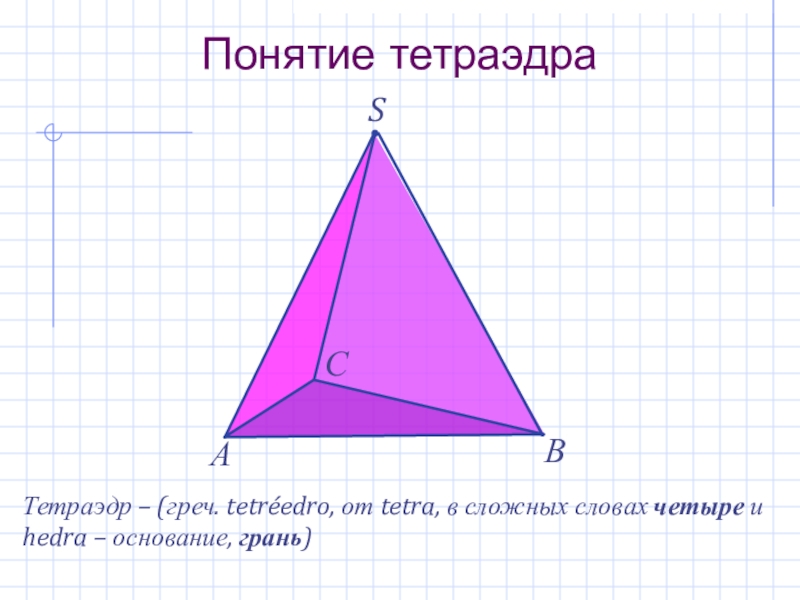
Слайд 5S
Понятие тетраэдра
А
В
С
Тетраэдр – (греч. tetréedro, от tetra, в сложных словах четыре
и hedra – основание, грань)
Слайд 9
Наклонный параллелепипед
Параллелепипед (от греч. παράλλος − параллельный и греч. επιπεδον −
плоскость) − призма, основанием которой служит параллелограмм, или многогранник, у которого шесть граней и каждая из них − параллелограмм.
Слайд 12
А
В
С
А1
D
D1
B1
C1
Свойства параллелепипеда (1)
Противоположные грани параллелепипеда параллельны и равны
Слайд 13О
Свойства параллелепипеда (2)
Диагонали параллелепипеда пересекаются в одной точке и делятся этой
точкой пополам
Слайд 14Прямой параллелепипед
Если боковые ребра параллелепипеда перпендикулярны плоскости основания, то такой параллелепипед
называется прямым
боковые грани – прямоугольники
Слайд 15Прямоугольный параллелепипед
Прямой параллелепипед, основания которого являются прямоугольниками называется прямоугольным
все грани –
прямоугольники
Слайд 16Свойства прямоугольного параллелепипеда
1° В прямоугольном параллелепипеде все шесть граней – прямоугольники
2° Все двугранные углы прямоугольного параллелепипеда– прямые
Слайд 17Прямоугольный параллелепипед
Длины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипеда
длина,
ширина и высота
Слайд 18Теорема о диагонали прямоугольного параллелепипеда
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов
трех его измерений:
d2 = a2 + b2 + c2
a
b
c
d
Следствие.
Диагонали прямоугольного параллелепипеда равны
Слайд 19Куб
Прямоугольный параллелепипед, все грани которого – равные квадраты называется кубом
все
грани – равные квадраты
d2 = 3a2
d
a
a
a
