Презентация, доклад по геометрии Способы нахождения площадей многоугольников

благородный,
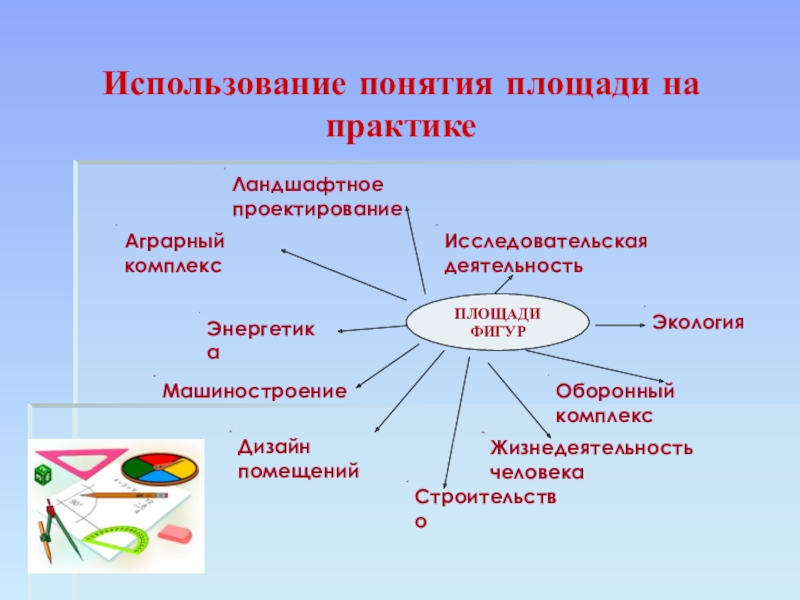
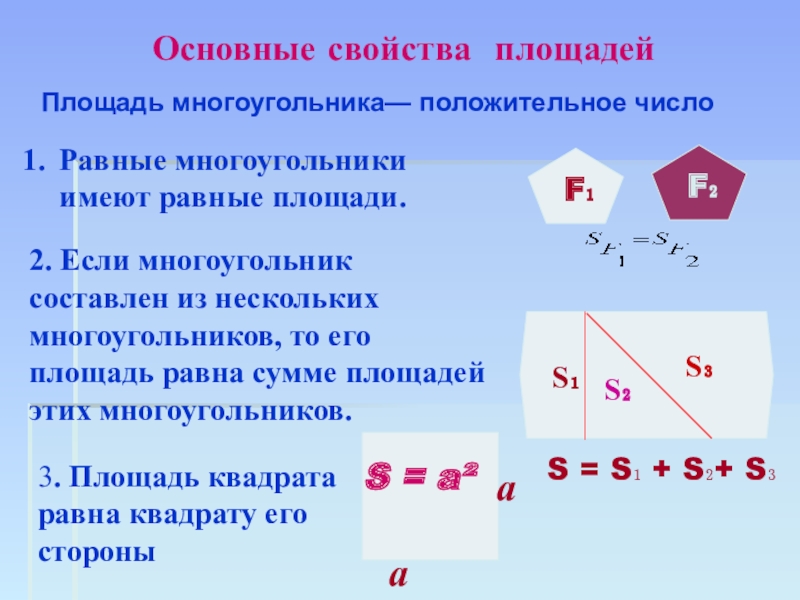
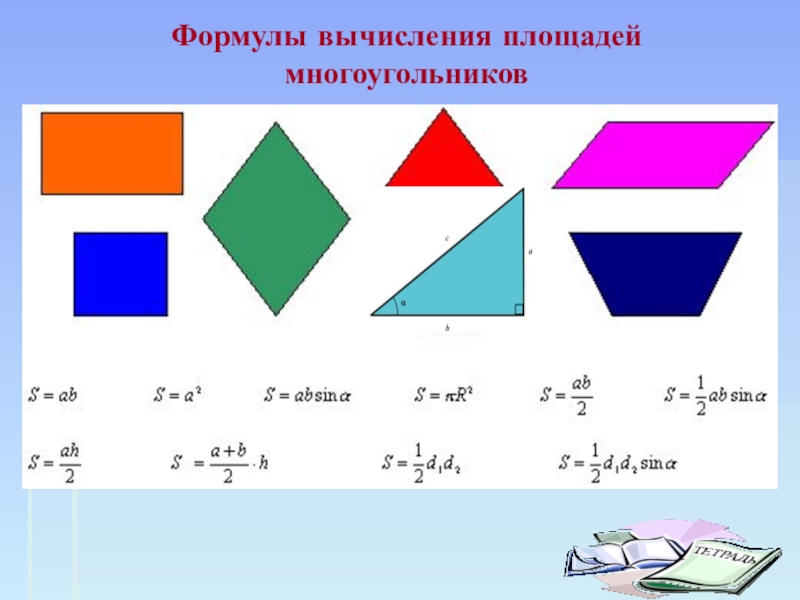
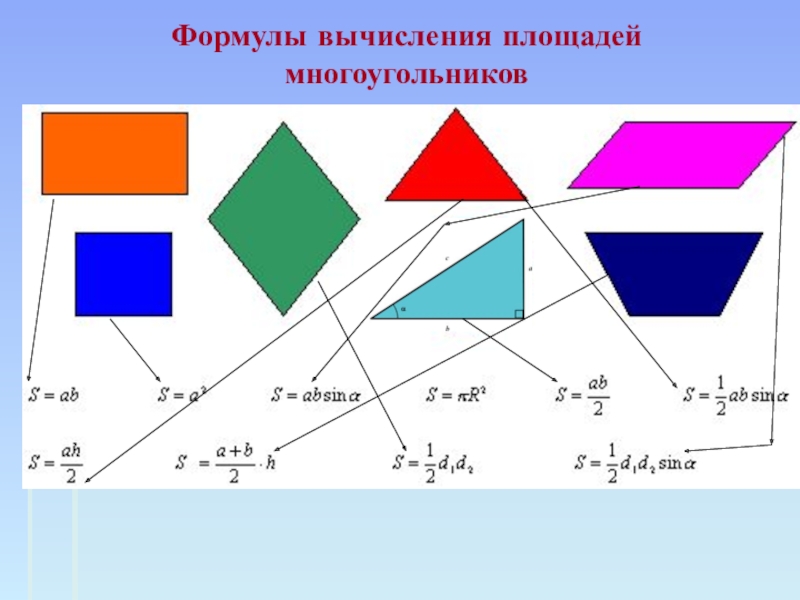
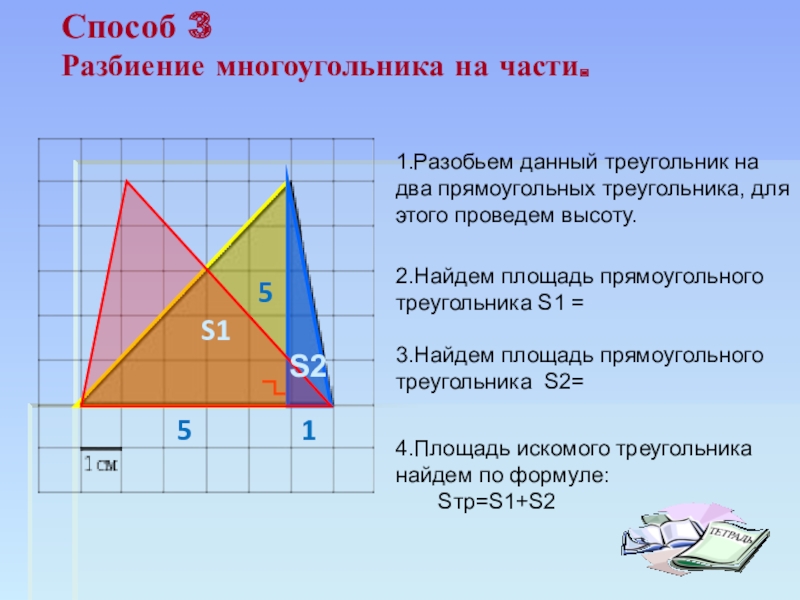
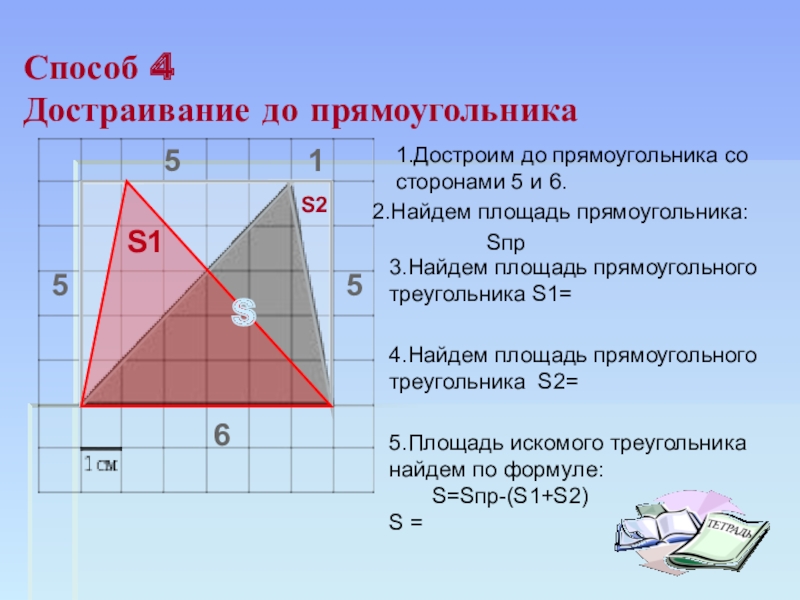
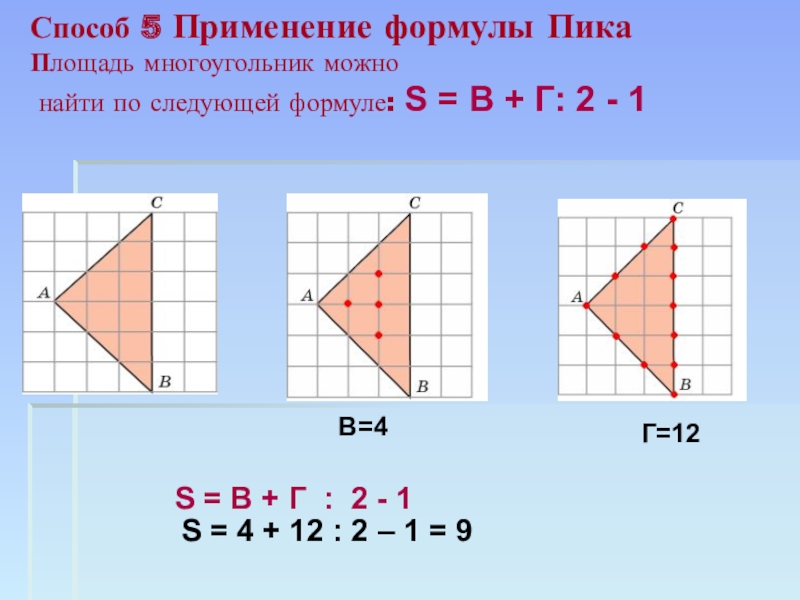
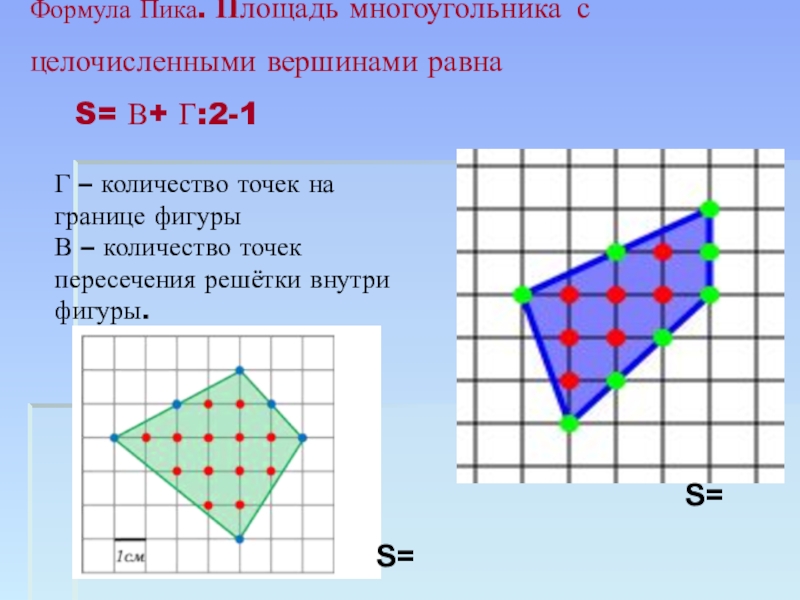
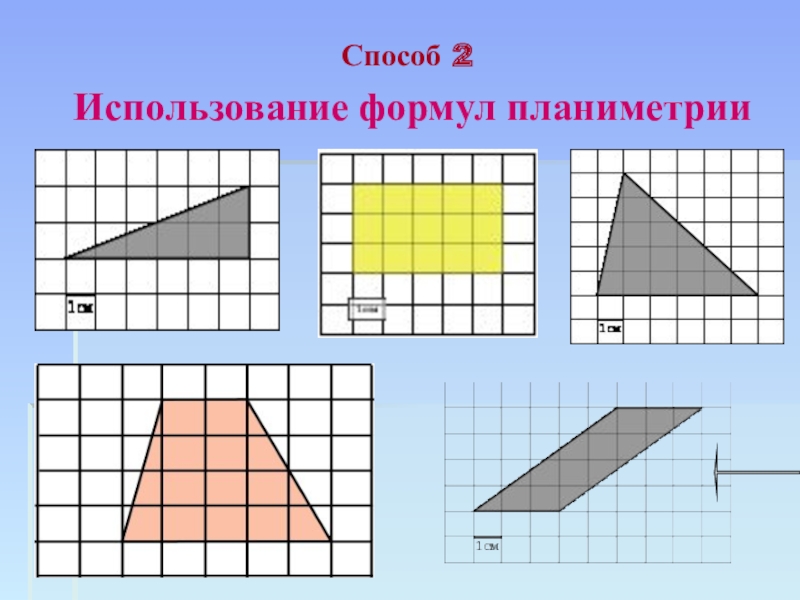
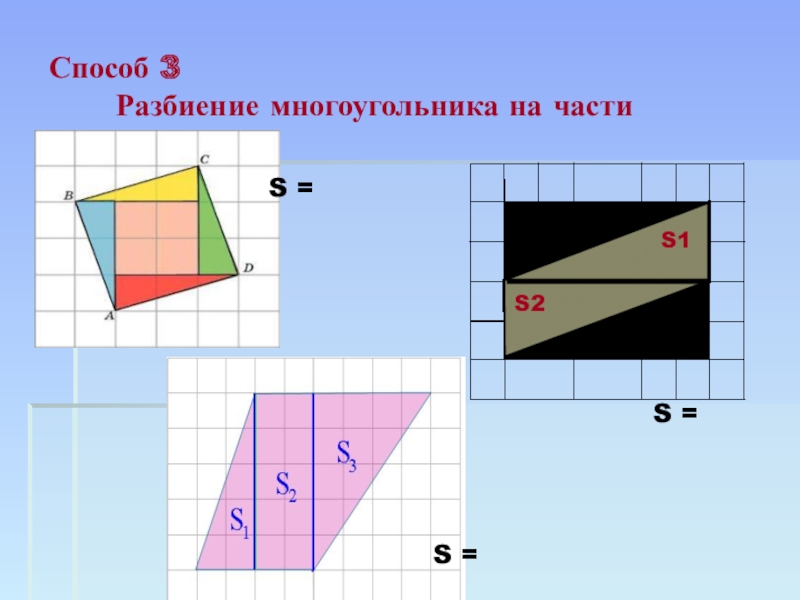
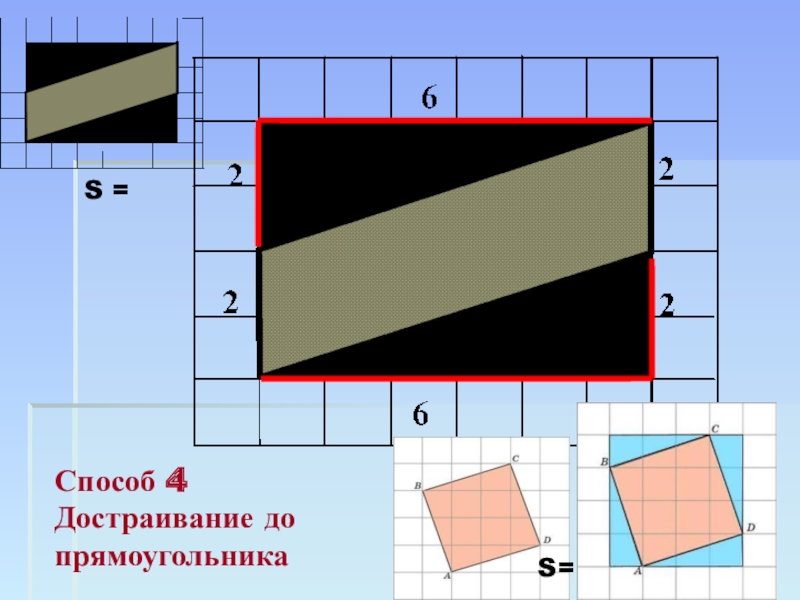
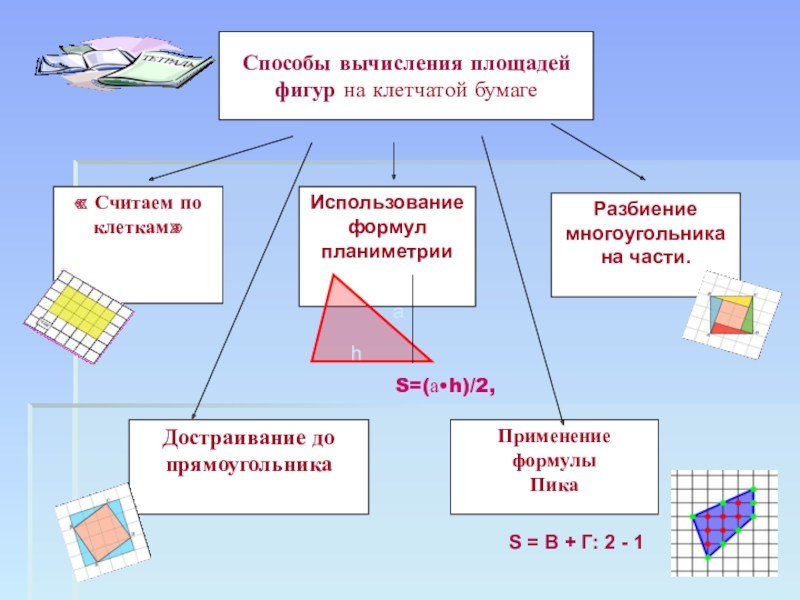
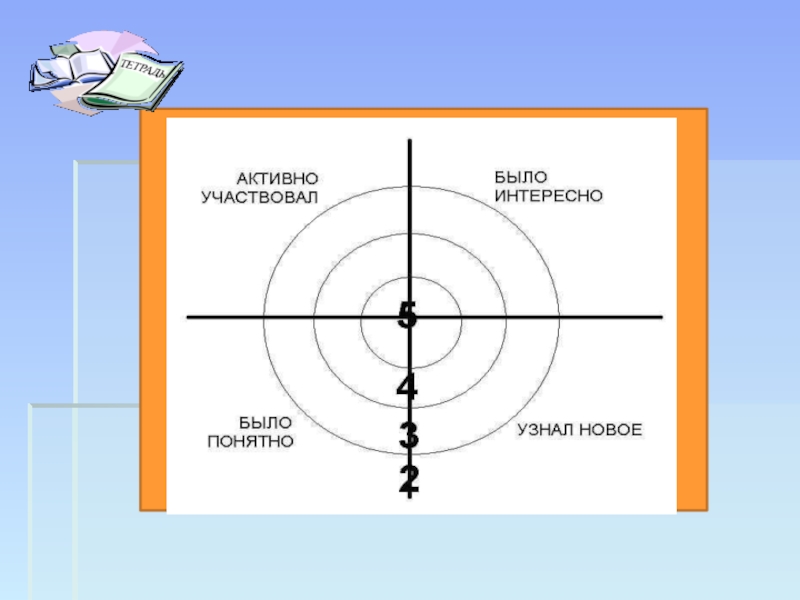
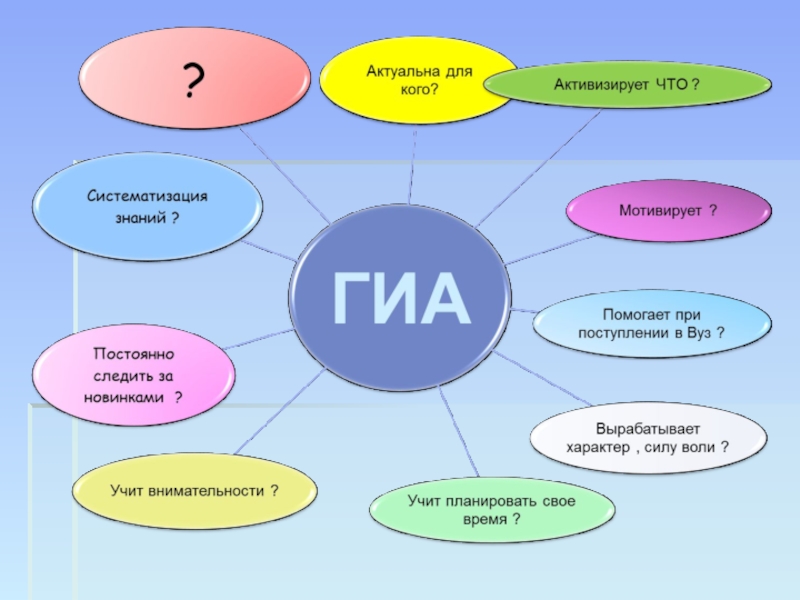
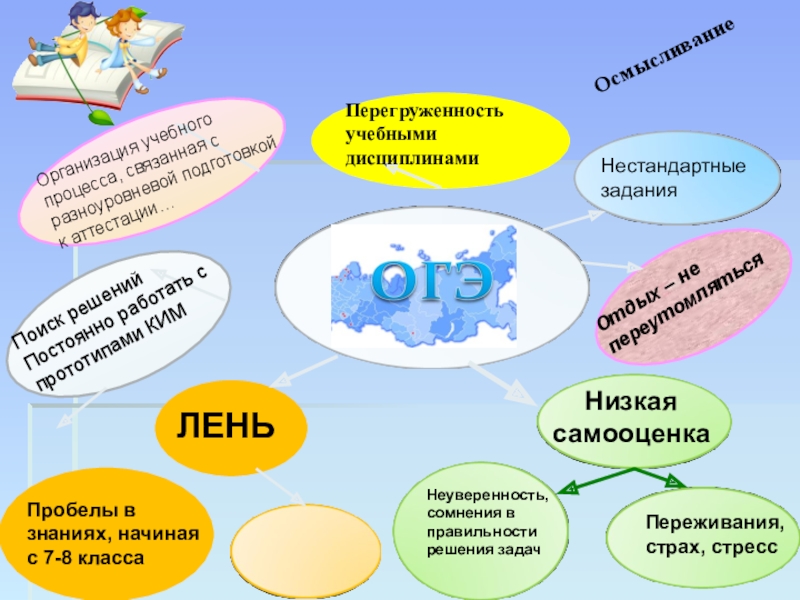
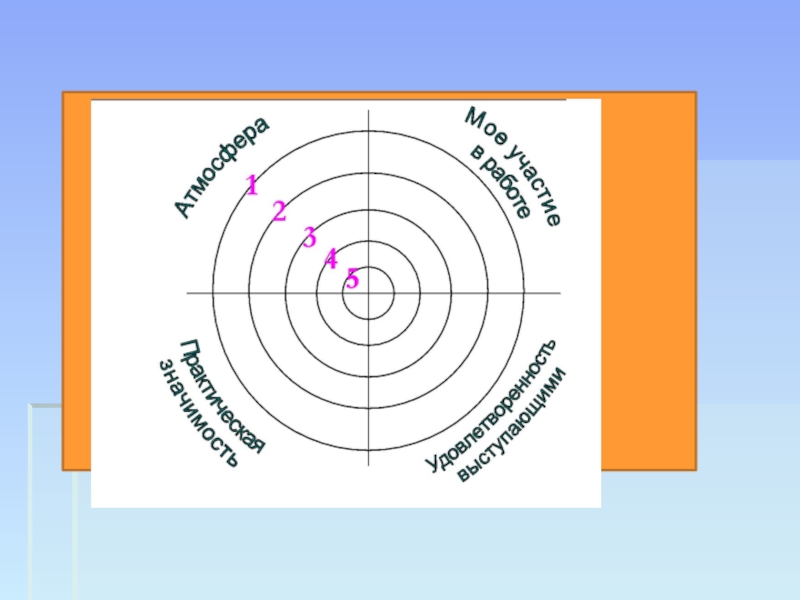
путь подражания – это путь самый легкий,
путь опыта – это путь самый горький.
(Конфуций)

Конфуций (Кун Фу-Цзы)— древний мыслитель и философ Китая жил примерно 2,5 тысячи лет назад. Конфуций известен как автор многочисленных мудрых изречений, в которых на все времена сформулированы основные правила жизни.

человека

ПЛОЩАДИ ФИГУР

задачи в конкретных случаях Задачи:

изучение и анализ информации по указанной теме;
поиск способов нахождения площадей многоугольников на клетчатой бумаге ;
решение заданий из открытого банка заданий ЕГЭ - показ практического применения результатов исследования.

многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

3. Площадь квадрата равна квадрату его стороны

S = S₁ + S₂+ S₃

a

a

S = a²

S₁

S₂

S₃

F₁

F₂

1 см х 1 см изображен треугольник (см. рис.).
Найдите его площадь в квадратных сантиметрах.

10

2.Дополним неполные клетки до полных клеток.

5

3. Сложим полученные количества полных клеток:

10+5=15

Ответ: 15

1

2

3

4

это ½ клетки

это ½ клетки

5

Способ 1

а – основание треугольника,

h – высота, проведенная к этому основанию.

а= , h=

Получаем
Sтр=

Способ 2 Использование формул планиметрии

площадь прямоугольного треугольника S1 =

3.Найдем площадь прямоугольного треугольника S2=

4.Площадь искомого треугольника найдем по формуле:
Sтр=S1+S2

5

1

5

S1

S2

Способ 3 Разбиение многоугольника на части.

площадь прямоугольного треугольника S1=

4.Найдем площадь прямоугольного треугольника S2=

5.Площадь искомого треугольника найдем по формуле:
S=Sпр-(S1+S2)
S =

Способ 4 Достраивание до прямоугольника

S

1899 году теорема Пика для расчёта площади многоугольника.

Площадь многоугольника
с целочисленными вершинами равна
S = В + Г: 2 - 1
где В - количество целочисленных точек внутри многоугольника,
Г — количество целочисленных точек на границе многоугольника.
Точка координатной плоскости называется целочисленной, если обе её координаты целые.

9

Способ 5 Применение формулы Пика Площадь многоугольник можно найти по следующей формуле: S = В + Г: 2 - 1

S = В + Г : 2 - 1

В+ Г:2-1

Г – количество точек на границе фигуры
В – количество точек пересечения решётки внутри фигуры.

S=

S=

многоугольника на части.

Достраивание до прямоугольника

Применение формулы Пика

1 см  x 1 см?
.

см  x 1 см

многоугольника на части.

Достраивание до прямоугольника

Применение формулы Пика

S=(а•h)/2,

S = В + Г: 2 - 1

а

h

учиться!

страх, стресс

Организация учебного процесса, связанная с разноуровневой подготовкой к аттестации…

ЛЕНЬ

Пробелы в знаниях, начиная с 7-8 класса

Нестандартные задания

Отдых – не переутомляться

Поиск решений Постоянно работать с прототипами КИМ

Осмысливание

стараться решить как можно больше вариантов заданий предыдущих лет.
Разумнее учить школьников общим универсальным приёмам и подходам к решению задач соответствующих типов.
Проверочное диагностическое  тестирование проводить по какой-то определённой теме.
   Переход  к комплексному тестированию разумен только в конце года (апрель-май), когда все темы изучены  и у учеников  накоплен запас общих подходов к основным типам заданий.
    Все тренировочные тесты следует проводить в режиме «теста скорости»,  т.е. с жестким ограничением времени. Можно всё время   фиксировать время,  чтобы ученик понял,  что  он успевает или не успевает выполнять за данный промежуток времени.

коммуникационная технология
Технология развития критического мышления
Проектная технология
Технология развивающего обучения
Здоровьесберегающие технологии  
Технология проблемного обучения
Игровые технологии
Модульная технология
Педагогика сотрудничества. 
Технологии уровневой дифференциации 
Традиционные технологии (классно-урочная система)

проблемы(создание проблемной ситуации)
4.Открытие новых знаний.
5.Первичное закрепление.
6.Самостоятельная работа с самопроверкой по эталону или образцу.
7.Включение нового знания в систему знаний( повторение).
8.Рефлексия деятельности.

в том, чтобы
научиться танцевать под дождем»