- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Решение задач
Содержание
№ 1104(а). Найти длину окружности описанной около правильного треугольника со стороной а.Выразите R через а.Подставьте в формулу длины окружности.
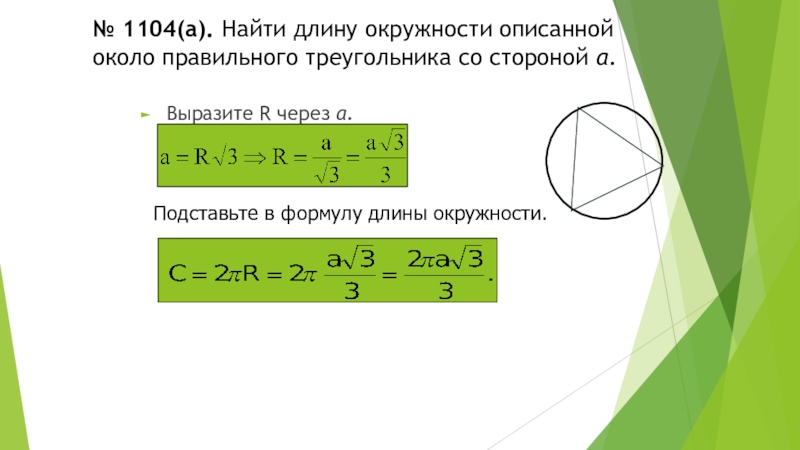
Слайд 2№ 1104(а). Найти длину окружности описанной около правильного треугольника со стороной
а.
Выразите R через а.
Подставьте в формулу длины окружности.
Слайд 3 R
O
R
H
R
H
Дано: АВС – равнобедренный, вписан в О(О; R); АВ=AС=b, BC=a.
№ 1104 (в). Найти длину окружности описанной около равнобедренного треугольника с основанием а и
А
В
С
ВН=
Из АВН: АН2=
Так как АО=R, то ОН=
стороной b.
Найти: С.
Решение. 1)
Слайд 4№ 1104 (в). Найти длину окружности описанной около равнобедренного треугольника с
основанием
Из ВОН: BО2=OH2+BH2=R2=
А
В
С
Н
C=
О
а и боковой стороной b.
Ответ:
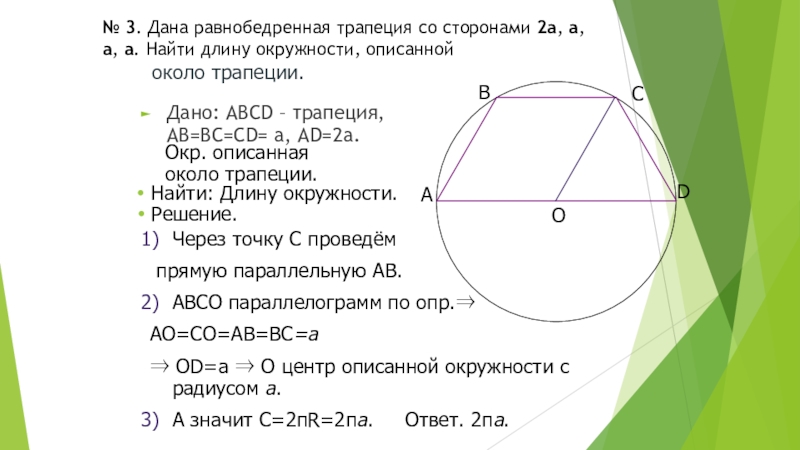
Слайд 5Через точку С проведём
прямую параллельную АВ.
АВСО параллелограмм по опр.
АО=СО=АВ=ВС=а
OD=a О центр описанной окружности с радиусом а.
А значит C=2R=2a. Ответ. 2a.
А значит C=2R=2a. Ответ. 2a.
№ 3. Дана равнобедренная трапеция со сторонами 2a, a, a, a. Найти длину окружности, описанной
Дано: АВСD – трапеция, АВ=ВС=СD= а, АD=2а.
около трапеции.
Найти: Длину окружности.
Решение.
Окр. описанная около трапеции.
D
О
