- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПЛОСКОСТЕЙ
Содержание
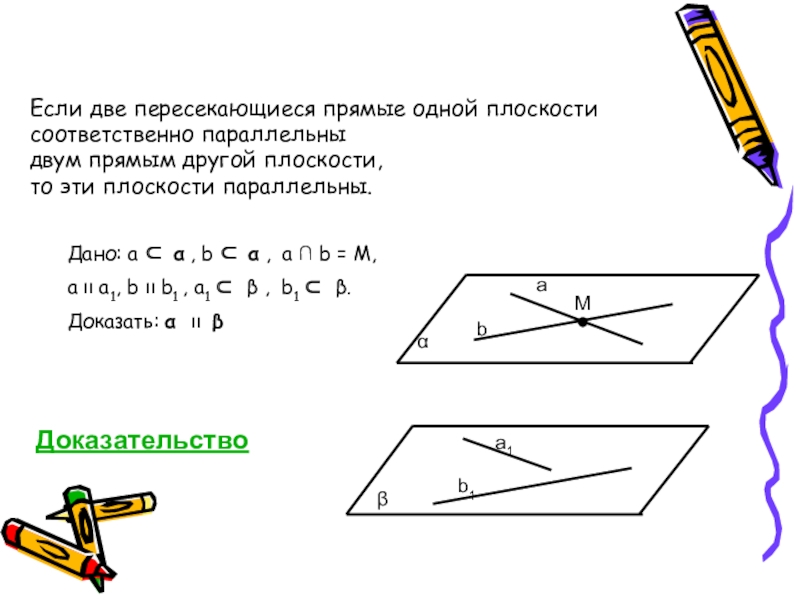
Если две пересекающиеся прямые одной плоскостисоответственно параллельны двум прямым другой плоскости,то эти плоскости параллельны.
Слайд 2
Если две пересекающиеся прямые одной плоскости
соответственно параллельны
двум прямым другой плоскости,
то
эти плоскости параллельны.
М
a
b
α
a1
b1
β
Доказательство
Дано: a ⊂ α , b ⊂ α , a ∩ b = M,
a װ a1, b װ b1 , a1 ⊂ β , b1 ⊂ β.
Доказать: α װ β
Слайд 3
Назад к теореме
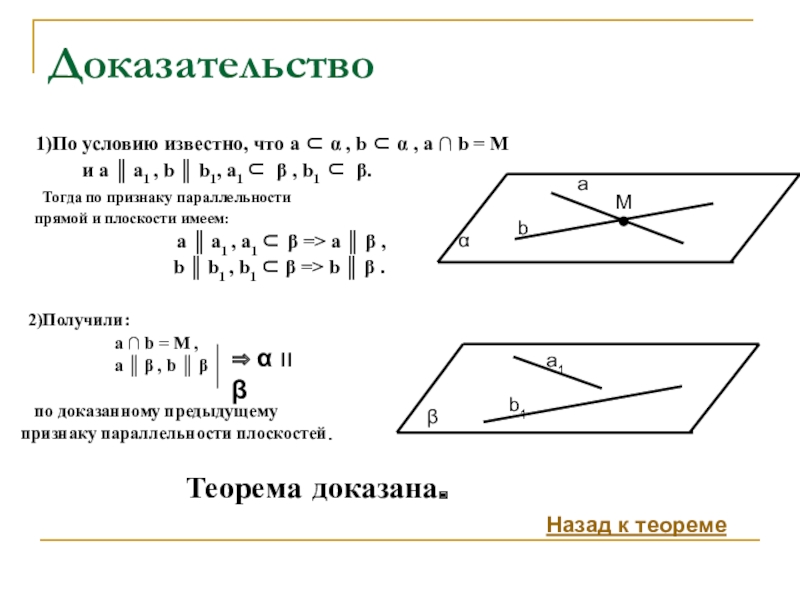
Доказательство
1)По условию известно, что a ⊂
α , b ⊂ α , a ∩ b = M
и a ║ a1 , b ║ b1, a1 ⊂ β , b1 ⊂ β.
Тогда по признаку параллельности
прямой и плоскости имеем:
a ║ a1 , a1 ⊂ β => a ║ β ,
b ║ b1 , b1 ⊂ β => b ║ β .
2)Получили:
a ∩ b = M ,
a ║ β , b ║ β
по доказанному предыдущему
признаку параллельности плоскостей.
Теорема доказана.
и a ║ a1 , b ║ b1, a1 ⊂ β , b1 ⊂ β.
Тогда по признаку параллельности
прямой и плоскости имеем:
a ║ a1 , a1 ⊂ β => a ║ β ,
b ║ b1 , b1 ⊂ β => b ║ β .
2)Получили:
a ∩ b = M ,
a ║ β , b ║ β
по доказанному предыдущему
признаку параллельности плоскостей.
Теорема доказана.
М
a
b
α
a1
b1
β
⇒ α װ β