- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Построение сечений параллелепипеда (11 класс)
Содержание
- 1. Презентация по геометрии Построение сечений параллелепипеда (11 класс)
- 2. Слайд 2
- 3. 6. Отрезки параллельных прямых, заключенные между параллельными
- 4. Для построения точки пересечения прямой и плоскости
- 5. Теорема. Если две точки прямой принадлежат плоскости,
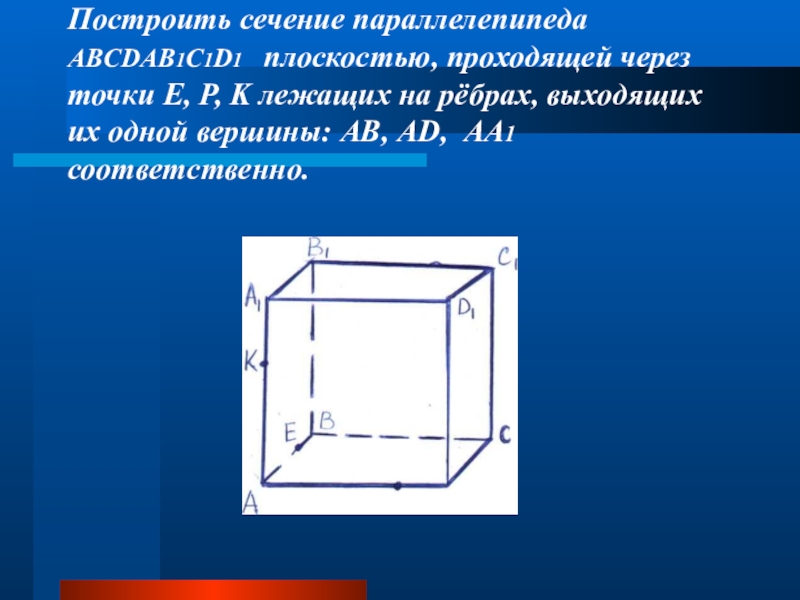
- 6. Построить сечение параллелепипеда ABCDAB1C1D1 плоскостью,
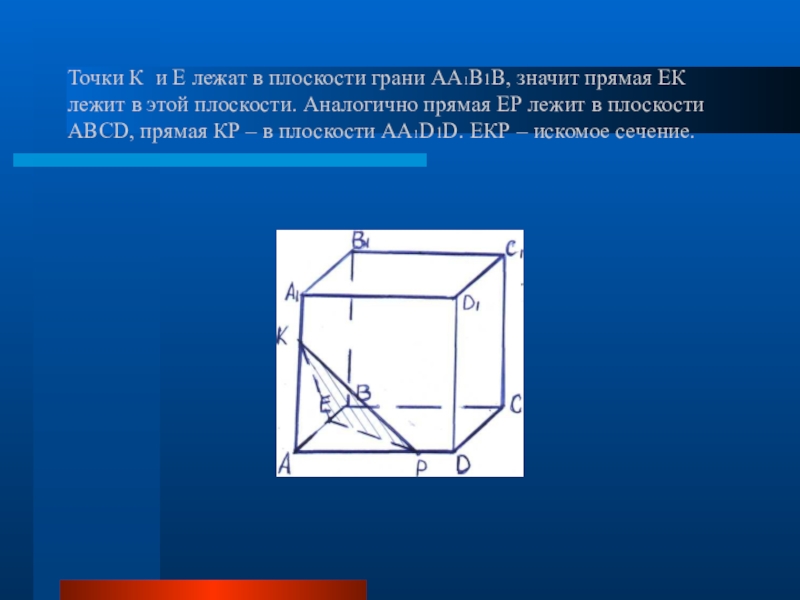
- 7. Точки К и Е лежат в плоскости
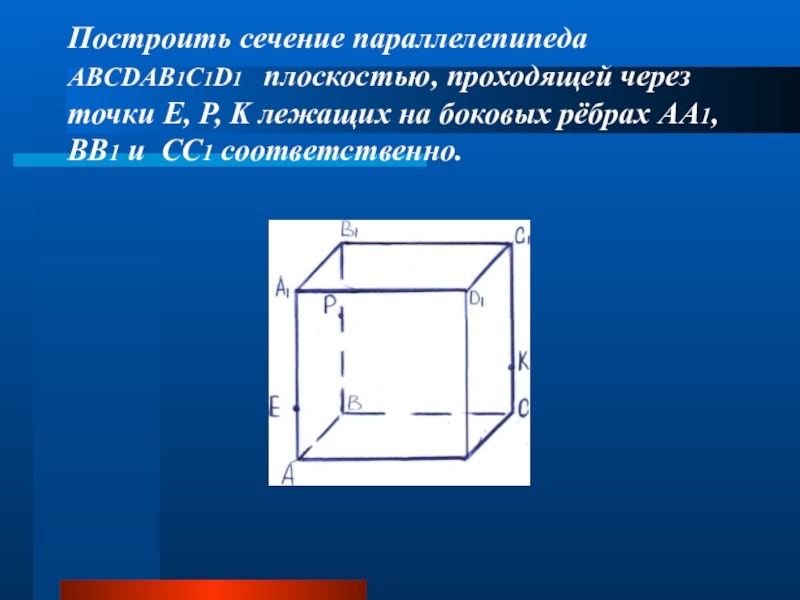
- 8. Построить сечение параллелепипеда ABCDAB1C1D1 плоскостью,
- 9. Построим отрезки ЕР, РК (пояснение как в предыдущей задаче).
- 10. Секущая плоскость пересекает параллельное грани по параллельным
- 11. Соединим точки Н и Т. Пятиугольник ЕРКНТ- искомое сечение
- 12. Построить сечение параллелепипеда ABCDAB1C1D1 плоскостью, проходящей
Слайд 1Тема урока: «Построение сечений параллелепипеда» Работу выполнила учитель математики МБОУ лицея № 3 Абдулова
Слайд 2 Вводный тест
Верно ли
а) Да; б) Нет.
Прямая а параллельна плоскости α. Выберите верное утверждение :
а) Прямая а не пересекает ни одну прямую, лежащую в плоскости α ;
б) Прямая а параллельна любой прямой, лежащую в плоскости α ;
в) Прямая а параллельна некоторой прямой, лежащей в плоскости α .
3. Прямая а параллельна плоскости α. Сколько прямых, лежащих в плоскости α, параллельны прямой а ?
а) таких прямых нет ;
б) одна прямая ;
в) бесконечное множество.
Прямая а пересекает плоскость α. Лежит ли в плоскости α хоть одна прямая, параллельна прямой а .
а) Да; б) Нет.
Одна из двух параллельных прямых параллельна некоторой плоскости. Верно ли утверждение, что и вторая прямая параллельна этой плоскости?
а) Да б) Нет.
Слайд 3
6. Отрезки параллельных прямых, заключенные между параллельными прямыми:
а) равны
б) не равны
в) пересекаются
7. Если стороны двух углов соответственно сонаправлены, то такие углы
а) смежные
б) соответственные
в) равны
г) не равны.
8. Какие многоугольники могут получиться в сечении тетраэдра:
а) треугольник, четырехугольник
б) треугольник, четырехугольник, пятиугольник
в) четырехугольник, пятиугольник
г) четырехугольник, пятиугольник, шестиугольник.
9. Выберите верное утверждение: существует параллелепипед, у которого:
а) только одна грань – прямоугольник
б) только две смежные грани – ромбы
в) все углы граней острые
г)все углы граней прямые
Слайд 4Для построения точки пересечения прямой и плоскости находят в плоскости прямую,
На рисунке изображены различные виды сечений приз и пирамид. Здесь выбраны самые простые фигуры
куб, тетраэдр и четырехугольная пирамиды.
Слайд 5
Теорема. Если две точки прямой принадлежат плоскости, то и вся прямая
Аксиома. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Слайд 6 Построить сечение параллелепипеда ABCDAB1C1D1 плоскостью, проходящей через точки E, P,
Слайд 7Точки К и Е лежат в плоскости грани АА1В1В, значит прямая
Слайд 8 Построить сечение параллелепипеда ABCDAB1C1D1 плоскостью, проходящей через точки E, P,
Слайд 10Секущая плоскость пересекает параллельное грани по параллельным отрезкам. Построим отрезки ЕТ
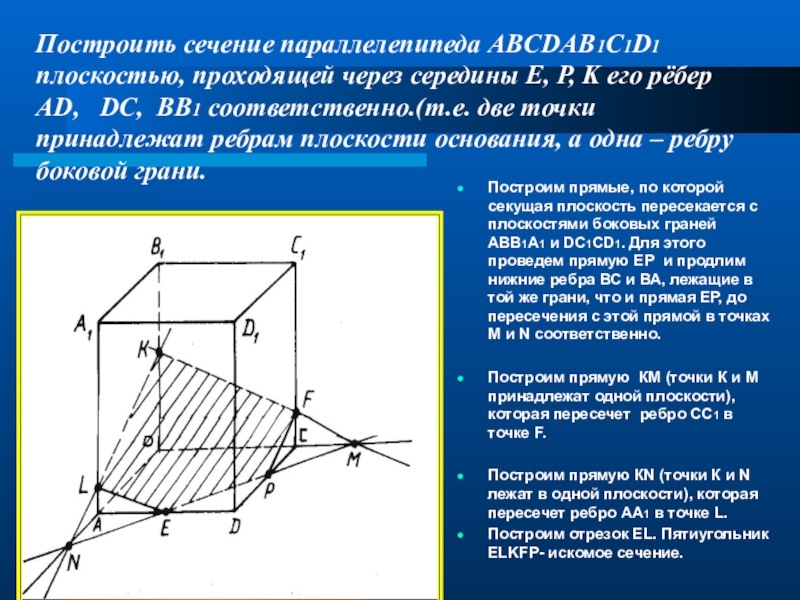
Слайд 12Построить сечение параллелепипеда ABCDAB1C1D1 плоскостью, проходящей через середины E, P,
Построим прямые, по которой секущая плоскость пересекается с плоскостями боковых граней АВВ1А1 и DС1СD1. Для этого проведем прямую ЕР и продлим нижние ребра ВС и ВА, лежащие в той же грани, что и прямая ЕР, до пересечения с этой прямой в точках М и N соответственно.
Построим прямую КМ (точки К и М принадлежат одной плоскости), которая пересечет ребро СС1 в точке F.
Построим прямую КN (точки К и N лежат в одной плоскости), которая пересечет ребро АА1 в точке L.
Построим отрезок ЕL. Пятиугольник ЕLKFP- искомое сечение.