- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме Взаимное расположение прямых и плоскостей
Содержание
- 1. Презентация по геометрии по теме Взаимное расположение прямых и плоскостей
- 2. Краткий план I. Взаимное расположение прямых в
- 3. Взаимное расположение прямых в пространстве
- 4. Прямые в пространстве могут:А) Быть параллельными
- 5. Прямые называются параллельными, если онилежат в одной
- 6. Две прямые называются скрещивающимися, если они не
- 7. Параллельность прямых и плоскостей Прямую называют
- 8. Свойства:Если плоскость проходит через данную прямую, параллельную
- 9. Перпендикулярность прямых в пространстве Две
- 10. ЛеммаЕсли одна из двух параллельных прямых перпендикулярна
- 11. Перпендикулярность прямой и плоскостиПрямая называется перпендикулярной к
- 12. Признак перпендикулярности прямой и плоскостиЕсли прямая перпендикулярна
- 13. Связь межу перпендикулярностью и параллельностью прямых в
- 14. Проекции и наклонные
- 15. Свойства наклонных и проекцийЕсли из одной точки
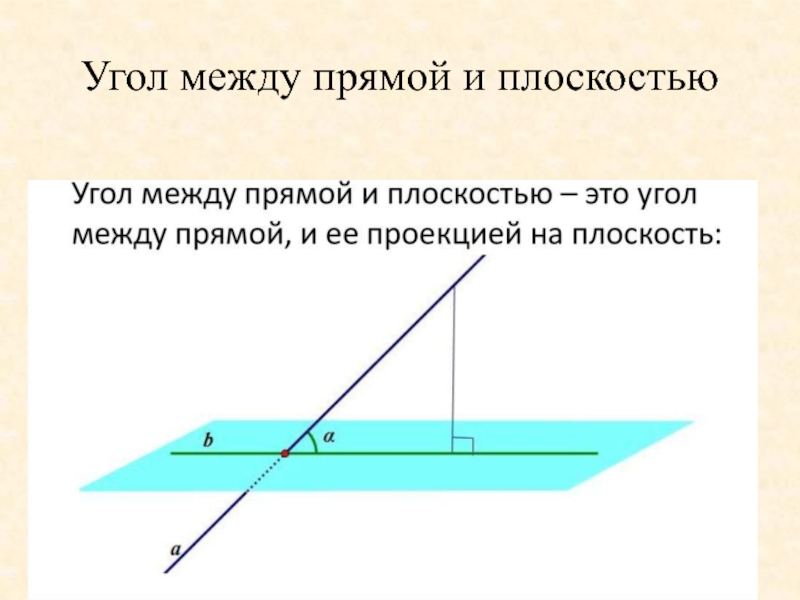
- 16. Угол между прямой и плоскостью
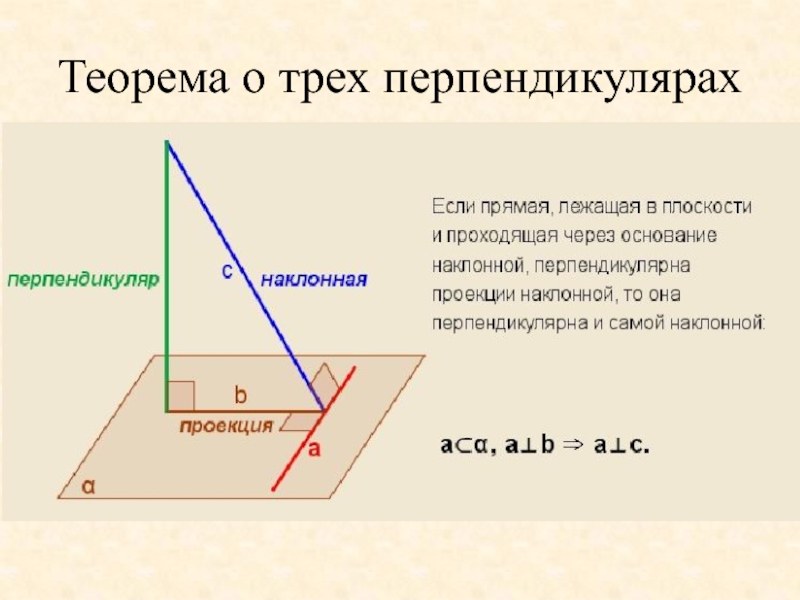
- 17. Теорема о трех перпендикулярах
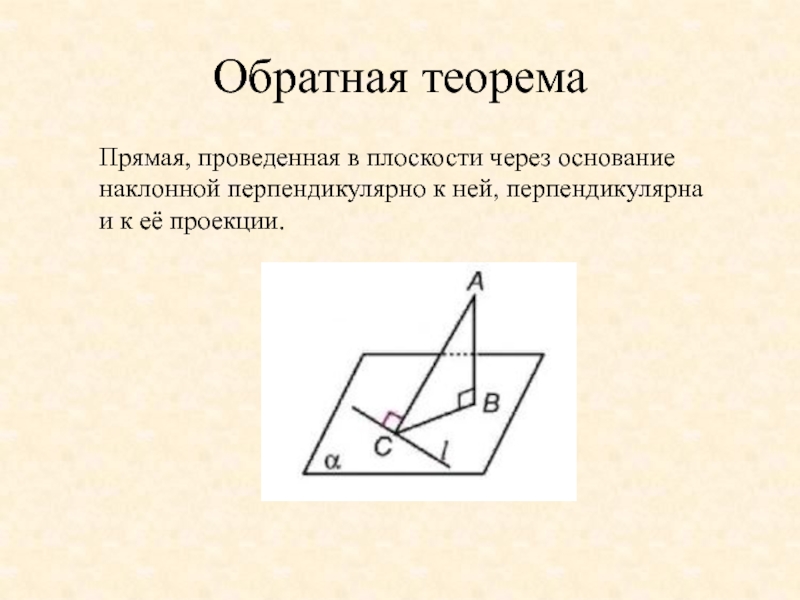
- 18. Обратная теоремаПрямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.
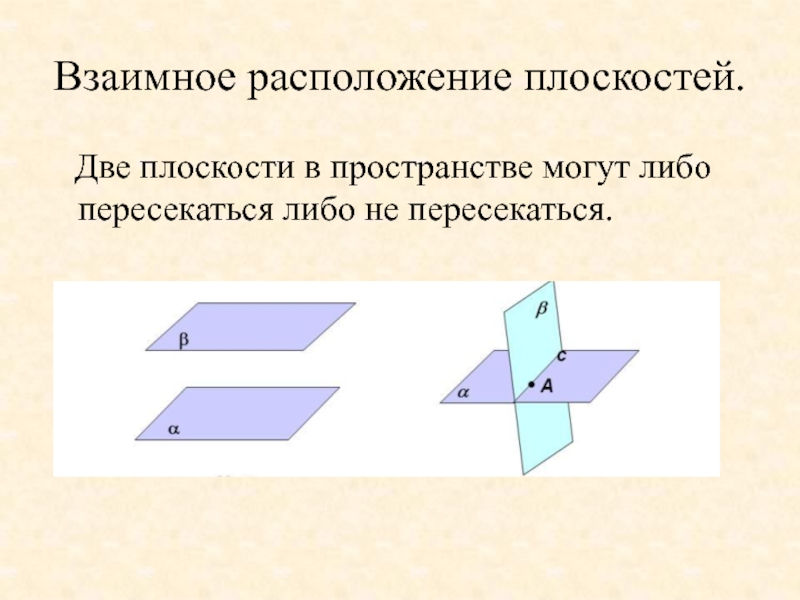
- 19. Взаимное расположение плоскостей. Две плоскости в пространстве могут либо пересекаться либо не пересекаться.
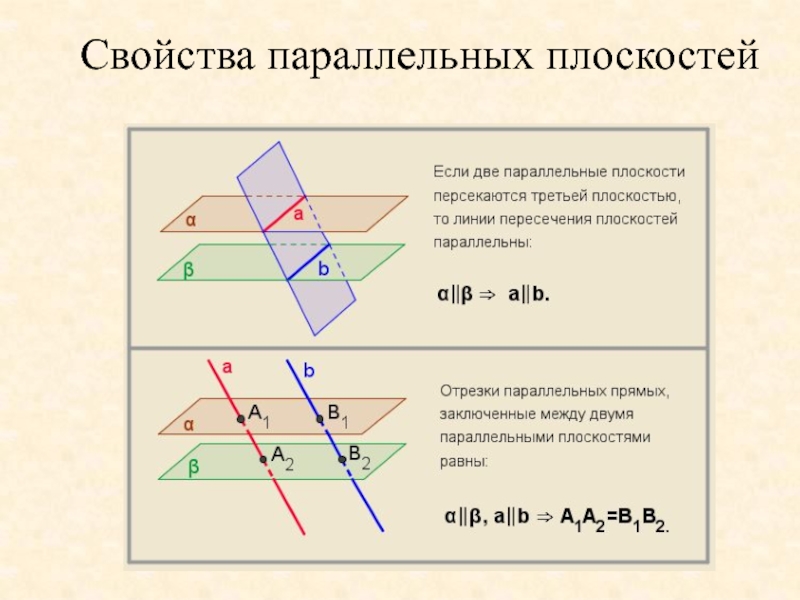
- 20. Параллельность плоскостей Две плоскости называются параллельными,
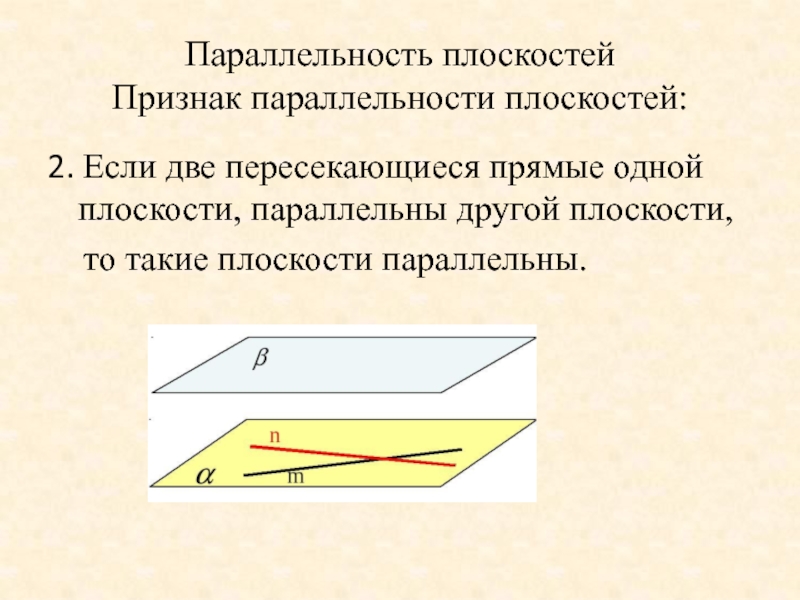
- 21. Параллельность плоскостей Признак параллельности плоскостей: 2.
- 22. Свойства параллельных плоскостей
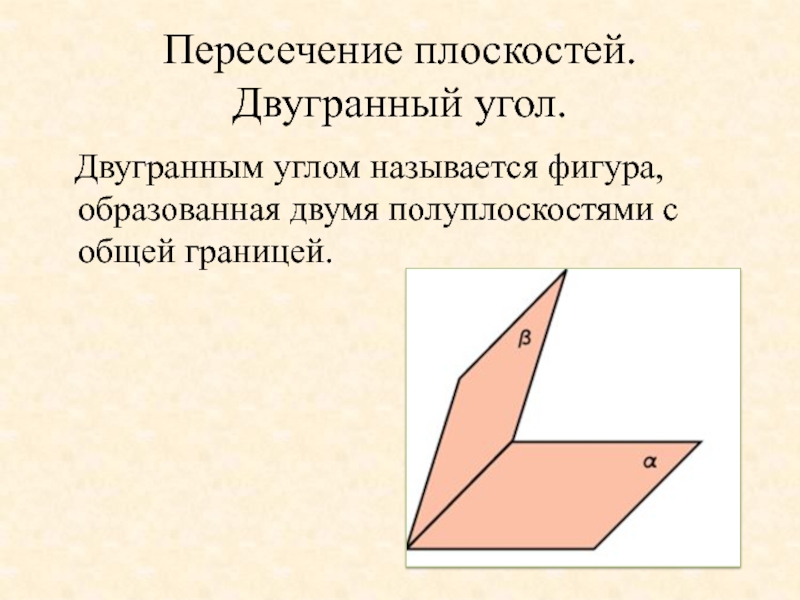
- 23. Пересечение плоскостей. Двугранный угол. Двугранным углом называется фигура, образованная двумя полуплоскостями с общей границей.
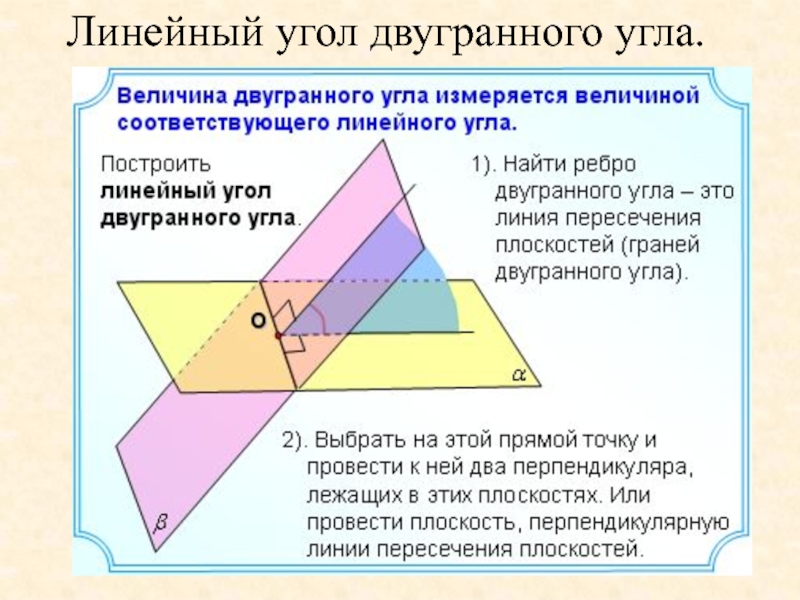
- 24. Линейный угол двугранного угла.
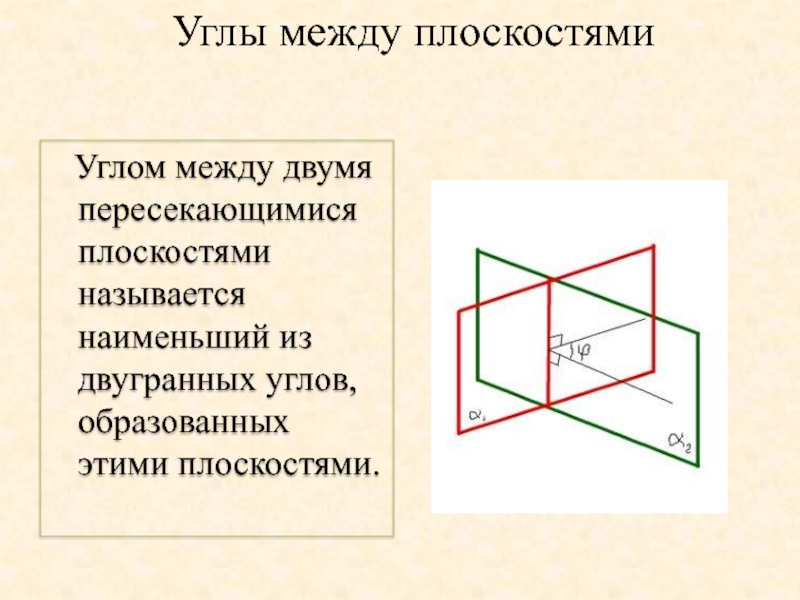
- 25. Углы между плоскостями Углом между двумя
- 26. Перпендикулярность плоскостей Две плоскости называются перпендикулярными,
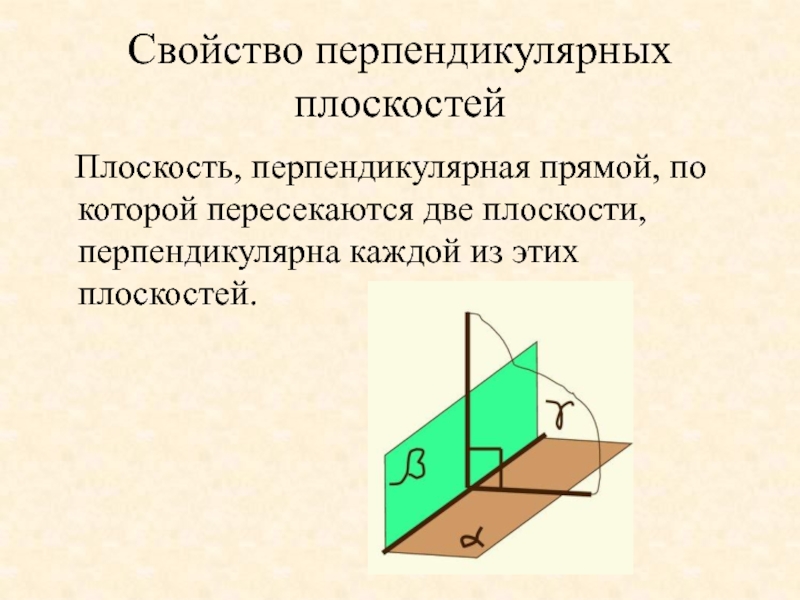
- 27. Свойство перпендикулярных плоскостей Плоскость, перпендикулярная прямой,
Слайд 1Взаимное расположение прямых и плоскостей.
Краткий теоретический материал для самостоятельного изучения темы.
Преподаватель
Лощинина С. А.
Слайд 2Краткий план
I. Взаимное расположение прямых в пространстве:
2. Скрещивающиеся прямые;
II. Взаимное расположение прямых и плоскостей:
1. Параллельность прямых и плоскостей
2. Перпендикулярность прямых и плоскостей
3. Проекции и наклонные
4. Угол между прямой и плоскостью
5. Теорема о трех перпендикулярах.
III. Взаимное расположение плоскостей.
Слайд 4
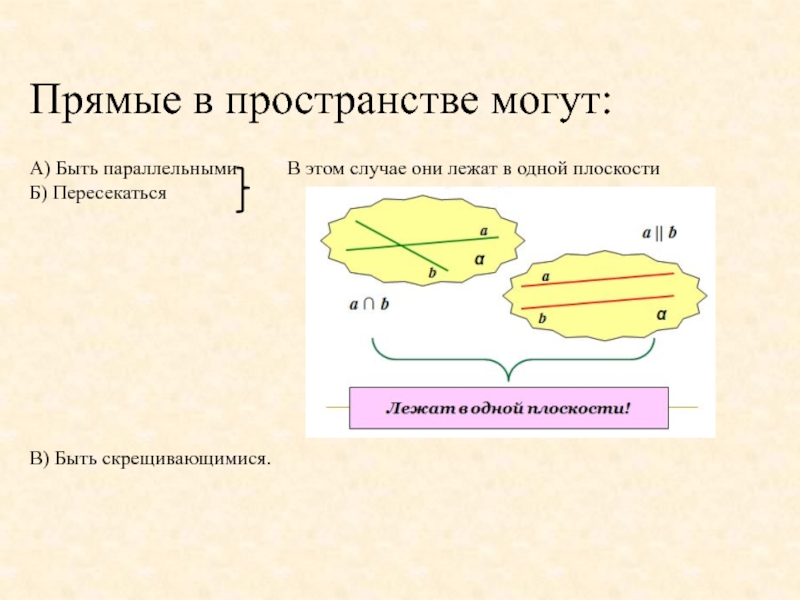
Прямые в пространстве могут:
А) Быть параллельными
Б) Пересекаться
В) Быть скрещивающимися.
Слайд 5Прямые называются параллельными, если они
лежат в одной плоскости и не имеют
пересечения.
Свойства:
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна
Если одна из параллельных прямых пересекает плоскость, то и вторая прямая также пересекает эту плоскость
Если две прямые параллельны третьей прямой, то они параллельны
Две параллельные прямые, как и две пересекающиеся прямые,
задают плоскость
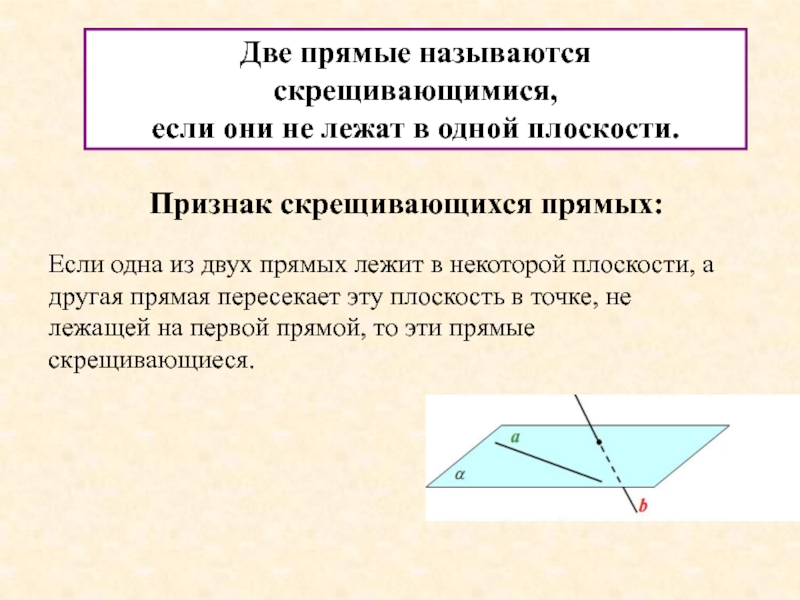
Слайд 6Две прямые называются
скрещивающимися,
если они не лежат в одной плоскости.
Признак
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Слайд 7Параллельность прямых и плоскостей
Прямую называют параллельной плоскости, если они
Признак параллельности прямой и плоскости
Если прямая, не лежащая в данной плоскости,
параллельна какой-нибудь прямой,
лежащей в этой плоскости , то
она параллельна и самой плоскости.
Слайд 8Свойства:
Если плоскость проходит через данную прямую, параллельную другой плоскости, то линия
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна этой плоскости, либо лежит в этой плоскости.
Слайд 9Перпендикулярность прямых в пространстве
Две прямые в пространстве называются
Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
(взаимно перпендикулярными),
если угол между ними равен 900.
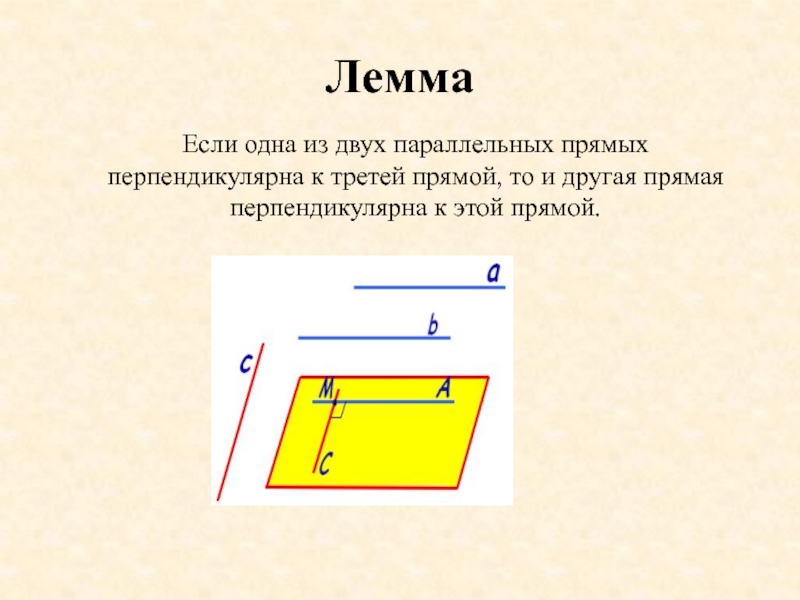
Слайд 10Лемма
Если одна из двух параллельных прямых перпендикулярна к третей прямой, то
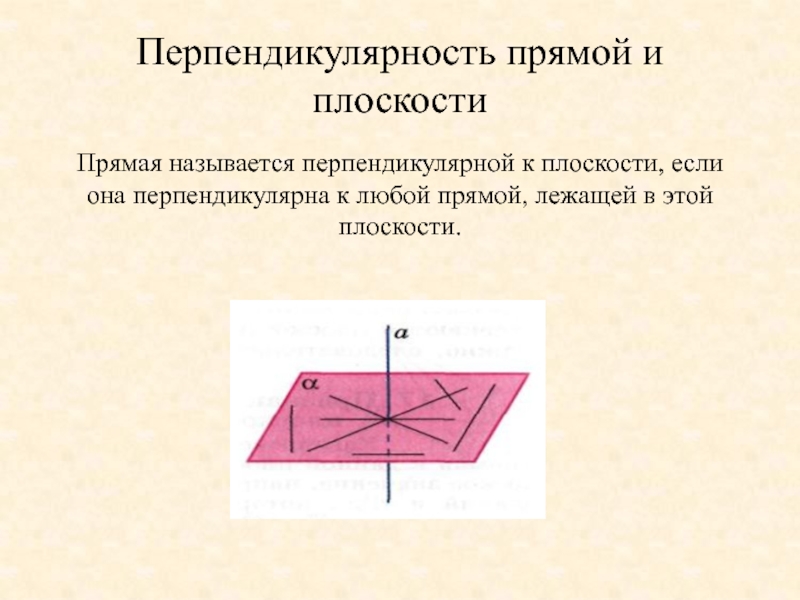
Слайд 11Перпендикулярность прямой и плоскости
Прямая называется перпендикулярной к плоскости, если она перпендикулярна
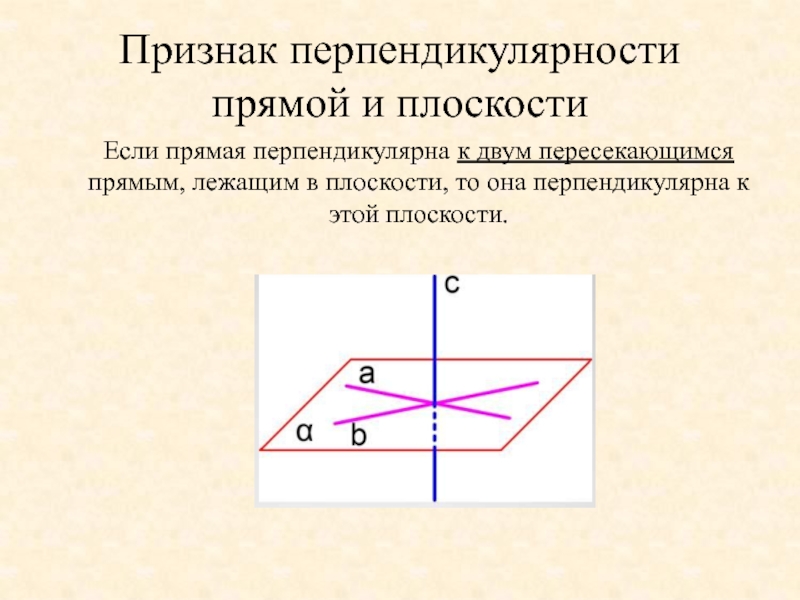
Слайд 12Признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна к двум пересекающимся прямым,
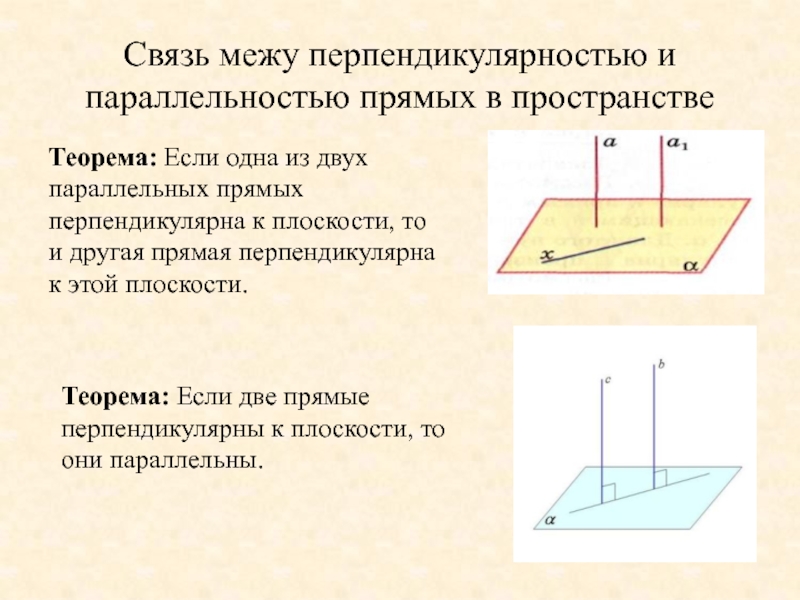
Слайд 13Связь межу перпендикулярностью и параллельностью прямых в пространстве
Теорема: Если одна из
Теорема: Если две прямые перпендикулярны к плоскости, то они параллельны.
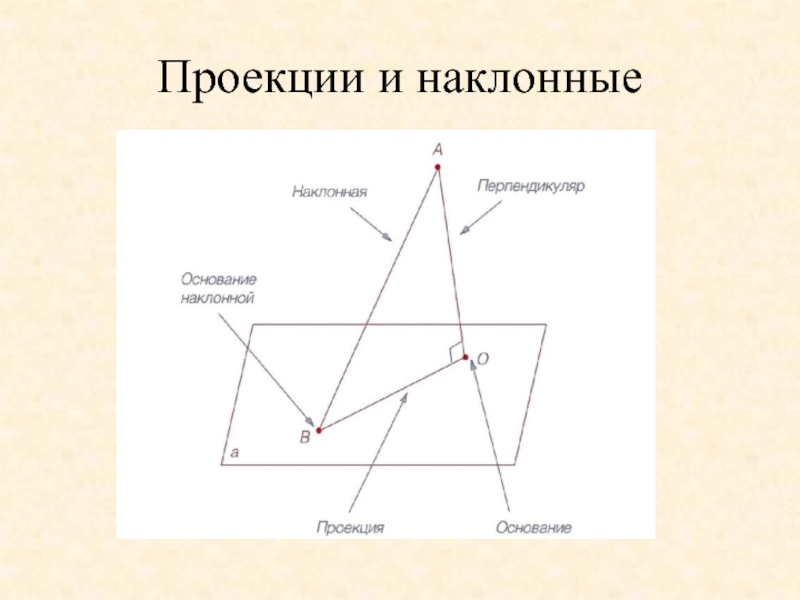
Слайд 15Свойства наклонных и проекций
Если из одной точки к плоскости проведены перпендикуляр
Любая наклонная больше перпендикуляра.
Равные наклонные имеют равные проекции.
Если проекции наклонных равны, то равны и наклонные.
Большей наклонной соответствует большая проекция и наоборот.
Слайд 18Обратная теорема
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней,
Слайд 19Взаимное расположение плоскостей.
Две плоскости в пространстве могут либо пересекаться
Слайд 20Параллельность плоскостей
Две плоскости называются параллельными, если у них нет
Признак параллельности плоскостей:
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны.
Слайд 21
Параллельность плоскостей
Признак параллельности плоскостей:
2. Если две пересекающиеся прямые одной плоскости, параллельны
то такие плоскости параллельны.
Слайд 23Пересечение плоскостей. Двугранный угол.
Двугранным углом называется фигура, образованная двумя
Слайд 25Углы между плоскостями
Углом между двумя пересекающимися плоскостями называется наименьший
Слайд 26Перпендикулярность плоскостей
Две плоскости называются перпендикулярными, если они пересекаются под
Признак перпендикулярности плоскостей: Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то такие плоскости перпендикулярны.