- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме Решение задач на некоторые свойства касательных,секущих и хорд
Содержание
- 1. Презентация по геометрии по теме Решение задач на некоторые свойства касательных,секущих и хорд
- 2. Слайды
- 3. Угол между касательной и хордойУгол между хордой
- 4. Слайд 4
- 5. Угол
- 6. Слайд 6
- 7. Слайд 7
- 8. Задача№2 Дано:АС, СЕ- секущие ∠АСЕ=32० ‿АЕ=100० ‿ВD-?Решение:1)
- 9. Угол
- 10. Слайд 10
- 11. Слайд 11
- 12. Следствие из теоремы о секущей №1Дано:
- 13. Задача№2 Если из одной точки проведены к
- 14. Слайд 14
- 15. Слайд 15
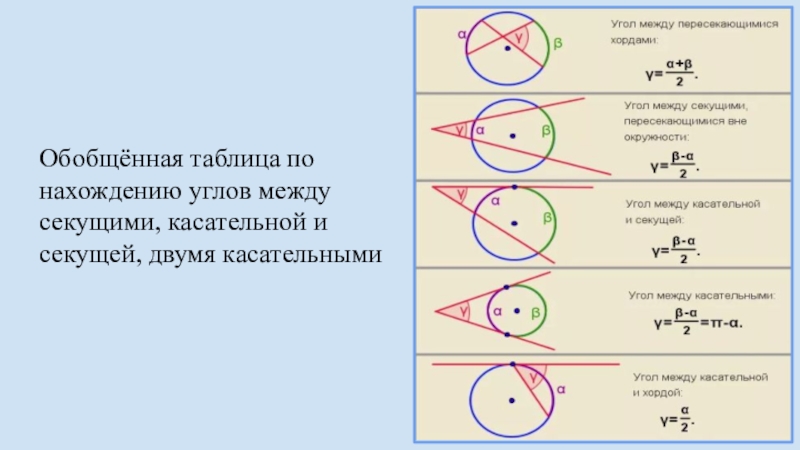
- 16. Обобщённая таблица по нахождению углов между секущими, касательной и секущей, двумя касательными
- 17. Над решением задач работали:Баранова Александра, Шиляева Маргарита,
Слайд 1 Совместный проект по геометрии 8 “Б” класса
“ Некоторые свойства касательных, хорд и секущих в окружности ”
2018
Слайд 2Слайды
3-4 Угол между касательной и хордой
5-6 Угол между секущими внутри окружности
7-8 Угол между секущими вне окружности
9-10 Угол между двумя касательными
11-12 Пересечение диаметра окружности и хорды
13-14 Следствие из теоремы о секущей (об отрезках хорд)№1
15-16 Следствие из теоремы о секущей (об отрезках хорд)№2
17 Сводная таблица теорем об углах в окружности
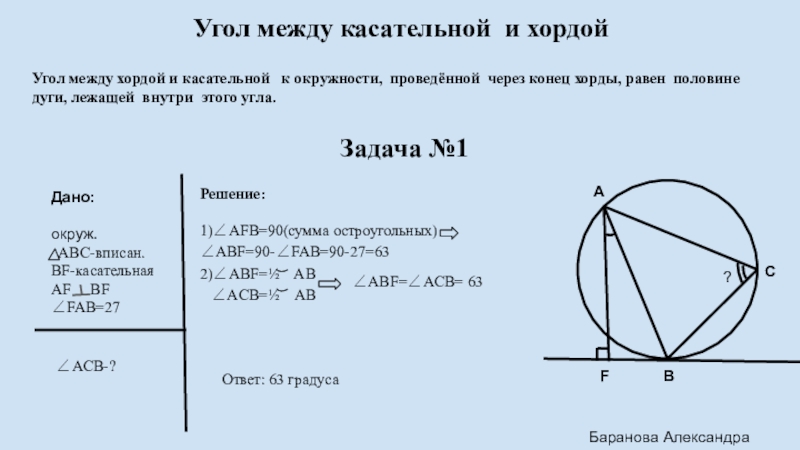
Слайд 3Угол между касательной и хордой
Угол между хордой и касательной к
Задача №1
Дано:
окруж.
ABC-вписан.
BF-касательная
AF BF
∠FAB=27
Баранова Александра
∠ACB-?
A
B
C
F
?
Решение:
1)∠AFB=90(сумма остроугольных) ∠ABF=90-∠FAB=90-27=63
2)∠ABF=½ AB
∠ACB=½ AB
∠ABF=∠ACB= 63
Ответ: 63 градуса
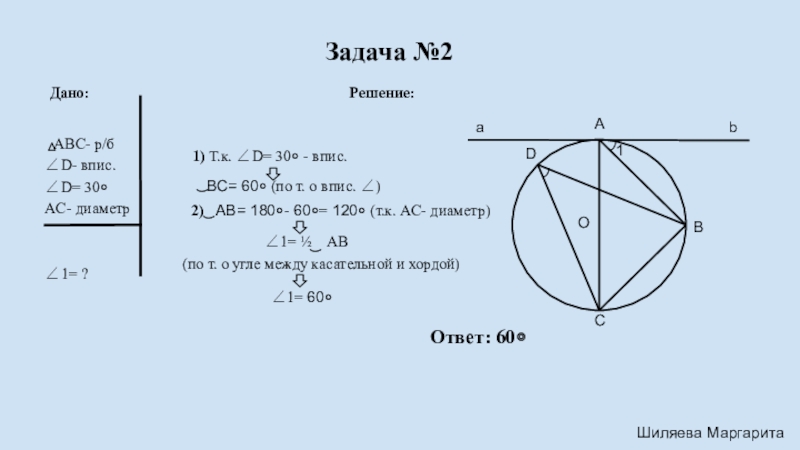
Слайд 4 Задача
Дано:
ABC- р/б
∠D- впис.
∠D= 30०
AC- диаметр
∠1= ?
Решение:
A
B
a
b
C
D
O
1
1) Т.к. ∠D= 30० - впис.
BC= 60० (по т. о впис. ∠)
2) AB= 180०- 60०= 120० (т.к. AC- диаметр)
∠1= ½ AB
(по т. о угле между касательной и хордой)
∠1= 60०
Ответ: 60०
Шиляева Маргарита
Слайд 5 Угол между секущими внутри окружности
Дано
∠DCB=50
∠ABC=20
Найти:
∠ DKB-?
Задача №1
Решение:
1.Т.к. ∠DCB-вписанный ‿ DB=100
‿AC= 40 (аналогично по теореме о вписанном угле)
2. По теореме об угле между секущими ∠ DKB=
(100 + 40 ) : 2 = 70
Ответ: 70
А
В
С
D
K
Слайд 6
Дано:
∠AMB-?
Решение:
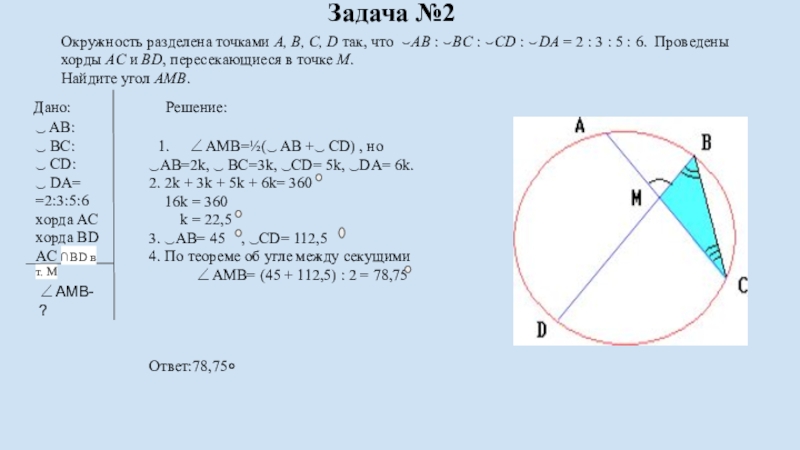
∠AMB=½(‿ AB +‿ CD) , но
‿AB=2k, ‿ BC=3k, ‿CD= 5k, ‿DA= 6k.
2. 2k + 3k + 5k + 6k= 360
16k = 360
k = 22,5
3. ‿AB= 45 , ‿CD= 112,5
4. По теореме об угле между секущими
∠AMB= (45 + 112,5) : 2 = 78,75
Ответ:78,75०
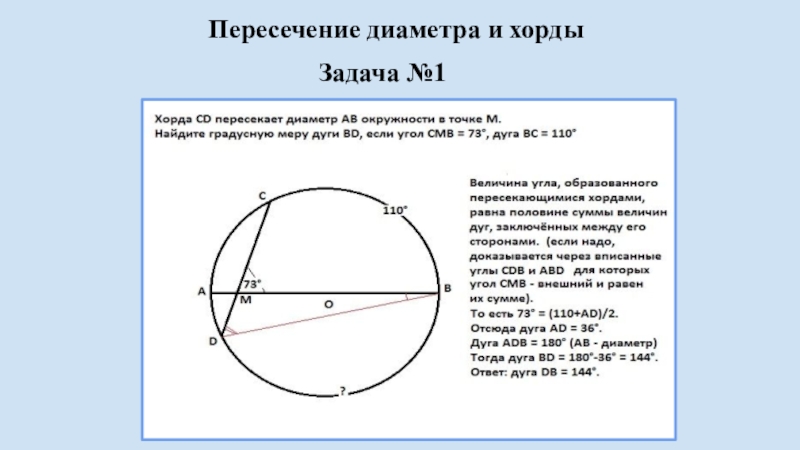
Окружность разделена точками A, B, C, D так, что ⌣AB : ⌣BC : ⌣CD : ⌣DA = 2 : 3 : 5 : 6. Проведены хорды AC и BD, пересекающиеся в точке M.
Найдите угол AMB.
‿ AB:
‿ BC:
‿ CD:
‿ DA=
=2:3:5:6
хорда AC
хорда BD
AC ⋂ BD в т. M
Слайд 7 Угол между
Если через точку, лежащую вне окружности проведены две секущие, то угол между ними измеряется полуразностью дуг, заключенных внутри угла.
Задача№1
Дано: Доказательство:
AC,AE-секущие 1)∠A=180०-(∠С+∠D) Доказать : 2)∠D=180०-∠CDE,∠CDE-вписанный
∠CAE=½(‿CE-‿BD) ∠CDE=1/2‿CE,∠D=180०-1/2‿CE
3)∠C-вписанный,∠С=1/2‿BD
4)∠A=180०-(180०-1/2‿CE+1/2‿BD)=180०-180०+½
‿CE-1/2‿BD=½(‿CE-‿BD)
Ч.Т.Д
Григорьев Кирилл
A
E
C
B
D
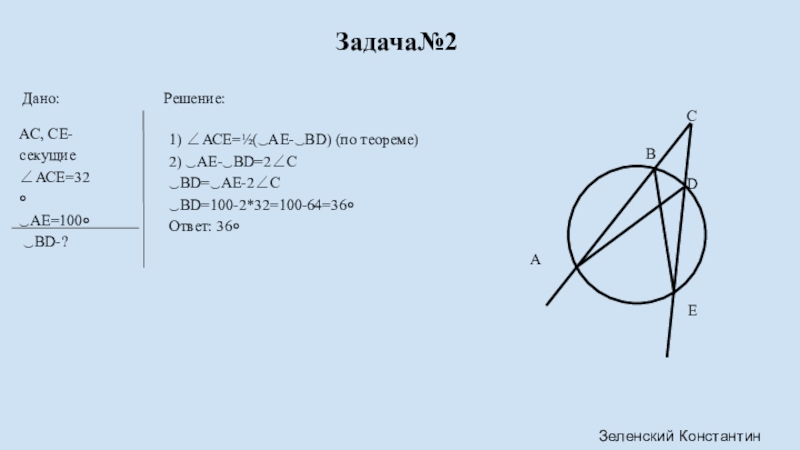
Слайд 8Задача№2
Дано:
АС, СЕ- секущие ∠АСЕ=32० ‿АЕ=100०
‿ВD-?
Решение:
1) ∠АСЕ=½(‿АЕ-‿ВD) (по теореме)
2)
‿BD=‿AE-2∠С
‿BD=100-2*32=100-64=36०
Ответ: 36०
C
A
E
B
D
Зеленский Константин
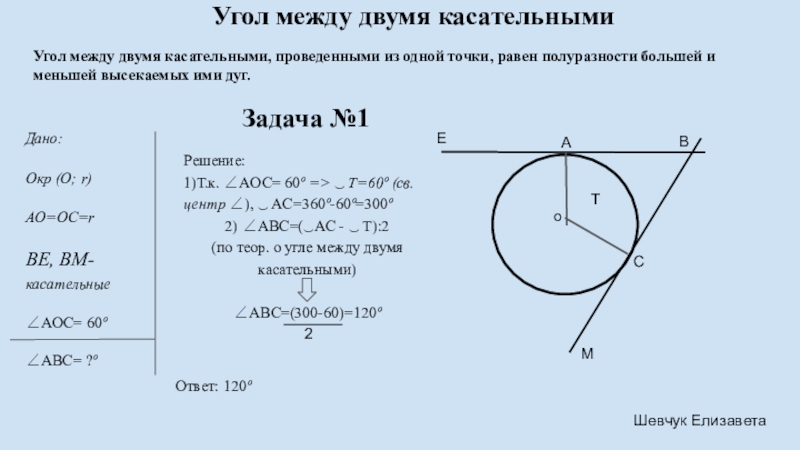
Слайд 9 Угол между двумя касательными
Дано:
Окр (О; r)
AO=OC=r
BE, BM- касательные
∠AOC= 60º
∠ABC= ?º
Решение:
1)Т.к. ∠AOC= 60º => ‿ T=60º (св. центр ∠), ‿ AC=360º-60º=300º
2) ∠ABC=(‿AC - ‿ T):2
(по теор. о угле между двумя касательными)
∠ABC=(300-60)=120º
Ответ: 120º
о
Т
А
Е
В
С
М
Угол между двумя касательными, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг.
Шевчук Елизавета
2
Слайд 10
Через концы А , В дуги окружности в 104 градуса проведены касательные АС и ВС. Найдите угол С . Ответ дайте в градусах.
Решение:
1)Доп.построение:
Проведём радиусы к точкам касания:
АО ⊥ АС и BO ⊥ ВС.
2)∠АОВ- центральный, опирающийся на ‿ АВ, значит ∠ АОВ = 104º
3) ‿ АКВ = 360 - 104 = 256
∠С = (256 - 104) : 2= 76
Ответ: 76º
Дано:
∠С = ?
AC;BC - касательные
‿ AB = 104º
А
О
В
С
Махонина Екатерина
К
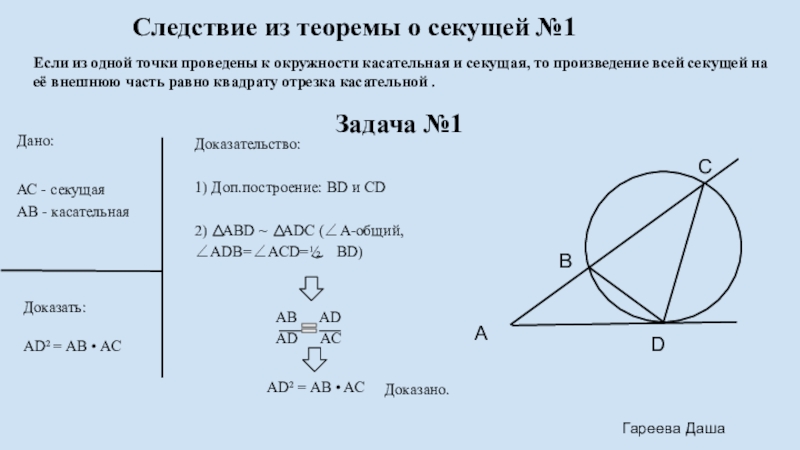
Слайд 12Следствие из теоремы о секущей №1
Дано:
АС - секущая
АВ - касательная
В
А
С
D
Доказать:
Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату отрезка касательной .
AD² = AB • AC
Доказательство:
1) Доп.построение: BD и CD
2) ABD ~ ADC (∠A-общий, ∠ADB=∠ACD=½ BD)
AB AD
AD AC
AD² = AB • AC
Доказано.
Гареева Даша
Задача №1
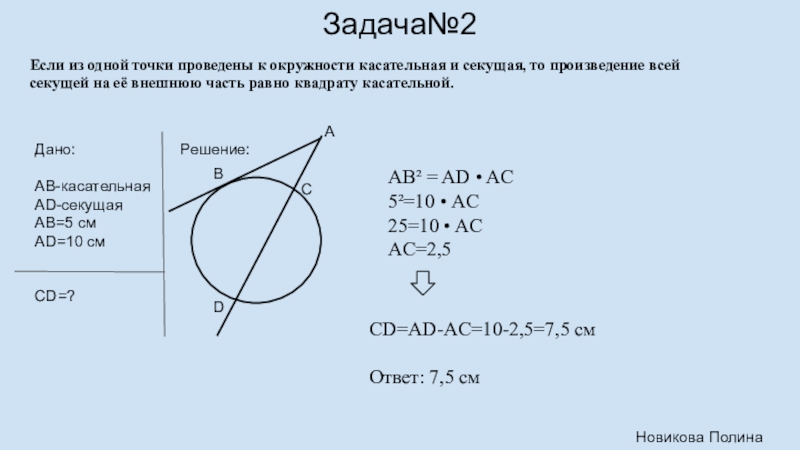
Слайд 13Задача№2
Если из одной точки проведены к окружности касательная и секущая,
Дано:
AB-касательная
AD-секущая
AB=5 см
AD=10 см
CD=?
Решение:
А
В
D
C
AB² = AD • AC
5²=10 • AC
25=10 • AC
AC=2,5
CD=AD-AC=10-2,5=7,5 см
Ответ: 7,5 см
Новикова Полина
Слайд 14 Следствие из теоремы
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. Если перевести это утверждение на язык букв (согласно рисунку справа), то получится следующее: AB * AC = AD *AE
Задача №1
Доказательство: Доп.построения
1.Проведём отрезки к BD и CD, Треугольники ABD и ADC подобны:
(угол A у них общий, а углы ADB и C равны, так как каждый из них
измеряется половиной дуги BD) .
2.Из подобия следует соотношение AB/AD = AD/AC,
3.Откуда получаем AD^2=AB * AC. Поскольку секущая выбрана произвольно, то данное соотношение будет выполняться для любой секущей. Следовательно доказана и теорема о двух секущих. Чибисов Денис
Чибисов Денис
Слайд 15
Из точки вне окружности проведена секущая, пересекающая окружность в точках, удаленных от данной на 12 и 20. Расстояние от данной точки до центра окружности равно 17. Найдите радиус окружности.
Дано:
Окр. с ц. - (.) О
АС и АЕ - секущие
АО = 17см
АВ = 12 см
АС = 20 см
R - ?
Решение:
OD=OE (радиусы)
т.к. АВ*АС = АD*АЕ (по св.-ву сек., провед. из точки к окр.)
12*20 = (17-OD)(17+OD)
2 2
12*20 = 17 - OD
OD = 7(см)
Ответ: 7 см.
Мукимова Алина