- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Основные задачи на построение.Урок №1. (7 класс.)
Содержание
- 1. Презентация по геометрии Основные задачи на построение.Урок №1. (7 класс.)
- 2. Цели урока:Рассмотреть основные (простейшие) задачи на построение:отложить
- 3. 1.Какой треугольник называется равнобедренным?2. Назовите признаки и
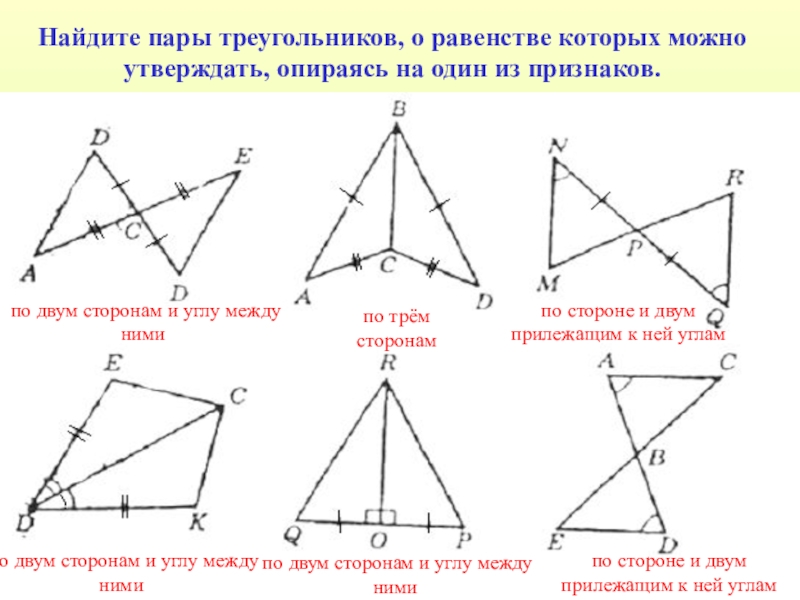
- 4. Найдите пары треугольников, о равенстве которых можно
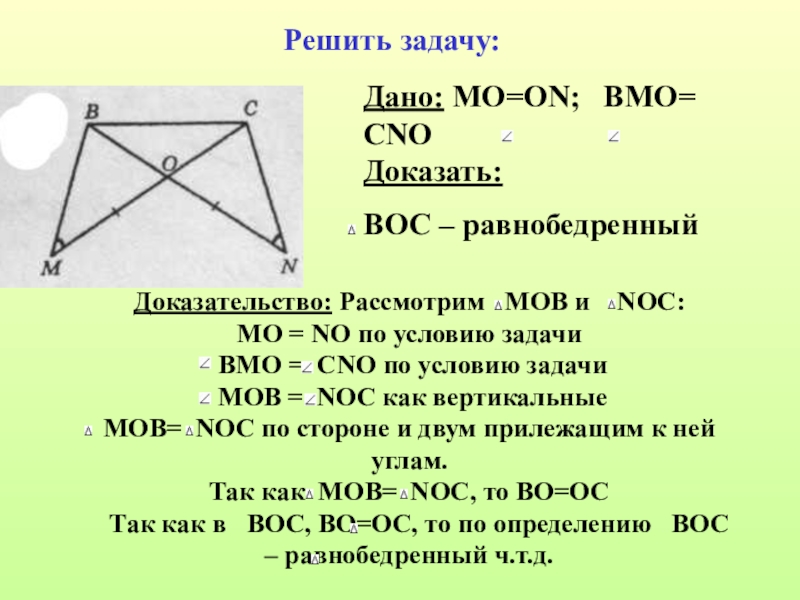
- 5. Решить задачу: Дано: МО=ON; BMO= CNO Доказать: ВОС – равнобедренный
- 6. Историческое введение. Первые задачи на построение
- 7. К задачам на построение прибегали древние
- 8. Задачи на построение помогали людям в
- 9. ПЛАТОНОсобенно сильно задачи на построение интересовали Платона,
- 10. Постановка проблемы урока Прочитайте задачи:
- 11. А теперь попробуйте выполнить эти же построения с помощью циркуля и линейки без делений.
- 12. Задачи на построение
- 13. Этапы решения задач на построение:Анализ (чертят рисунок
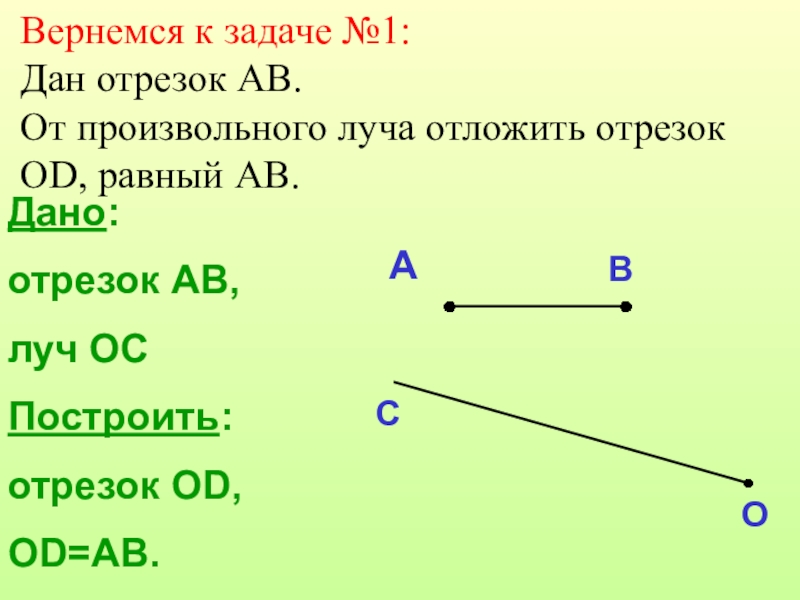
- 14. Дано: отрезок АВ,луч ОСПостроить: отрезок ОD,OD=AB.ABCOВернемся к
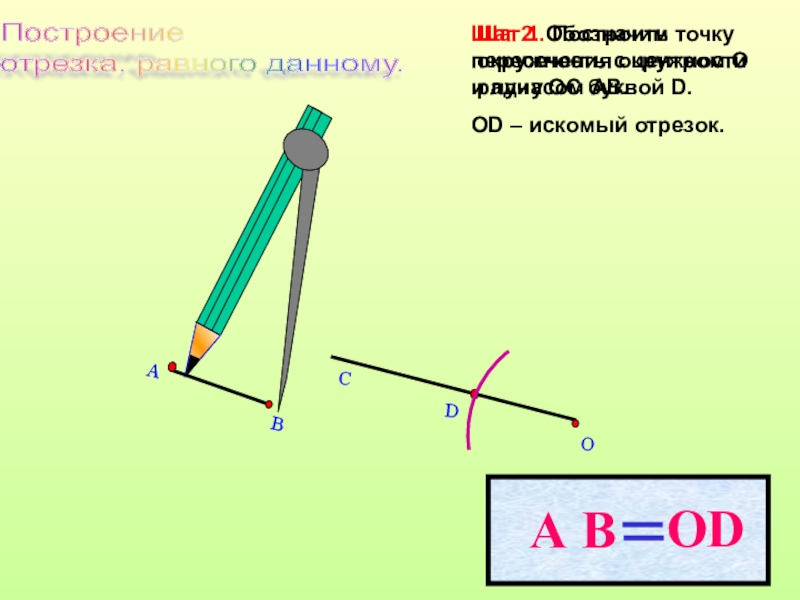
- 15. DОCШаг 2. Обозначим точку пересечения окружности и
- 16. Дано: прямая a ,Построить: РМ аМ
- 17. Шаг 2. Из точек А и В
- 18. aNBACМПосмотрим на расположение циркулей.АМ=АN=MB=BN, как равные радиусы. МN-общая сторона. MВN= MAN, по трем сторонам
- 19. Слайд 19
- 20. Дано: прямая a ,Построить: РМ аМ
- 21. МaШаг 3. Проведём прямую PQ,которая и будет
- 22. Докажем, что а РМАМ=МВ, как радиусы
- 23. Спасибо за урок
Слайд 1учитель математики МБОУ Фёдоровская СОШ
Архипова Ирина Александровна
Геометрия
7 класс
Основные задачи
Слайд 2Цели урока:
Рассмотреть основные (простейшие) задачи на построение:
отложить отрезок, равный данному;
построить
построить прямую, перпендикулярную к данной прямой.
Слайд 31.Какой треугольник называется равнобедренным?
2. Назовите признаки и свойства равнобедренного треугольника.
3. Сформулируйте
Устная работа:
4. Что называется серединным перпендикуляром?
Слайд 4Найдите пары треугольников, о равенстве которых можно утверждать, опираясь на один
по двум сторонам и углу между ними
по стороне и двум прилежащим к ней углам
по трём сторонам
по двум сторонам и углу между ними
по двум сторонам и углу между ними
по стороне и двум прилежащим к ней углам
Слайд 6Историческое введение.
Первые задачи на построение возникли в глубокой древности.
Уже древним архитекторам и землемерам приходилось решать простейшие задачи на построение, связанные с их профессией.
Слайд 7 К задачам на построение прибегали древние инженеры, когда составляли рабочий
Слайд 8
Задачи на построение помогали людям в их хозяйственной жизни, их
Слайд 9ПЛАТОН
Особенно сильно задачи на построение интересовали Платона, основателя знаменитой "Академии" в
Платон и его ученики считали построение геометрическим, если оно выполнялось при помощи циркуля и линейки, т. е. путем проведения окружностей и прямых линий. Если же в процессе построения использовались другие чертежные инструменты, то построение не считалось геометрическим. Древние греки вслед за Платоном стремились к геометрическим построениям и считали их идеалом в геометрии.
Слайд 10Постановка проблемы урока Прочитайте задачи: Задача №1: Дан отрезок АВ. От произвольного
Слайд 12Задачи на построение
решении которых нужно построить геометрическую фигуру, удовлетворяющую условию задачи с помощью циркуля и линейки без делений.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Слайд 13Этапы решения задач на построение:
Анализ (чертят рисунок искомой фигуры, устанавливающий связи
Построение (по намеченному плану выполняют построение циркулем и линейкой).
Доказательство (нужно доказать,что построенная фигура удовлетворяет условиям задачи).
Исследование (нужно исследовать при любых ли данных задача имеет решение, и если имеет, то сколько).
В 7 классе мы с вами решаем самые простые задачи на построение, поэтому иногда достаточно только второго пункта схемы ( или второго и третьего).
Слайд 14
Дано:
отрезок АВ,
луч ОС
Построить:
отрезок ОD,
OD=AB.
A
B
C
O
Вернемся к задаче №1:
Дан отрезок
Слайд 15D
О
C
Шаг 2. Обозначим точку пересечения окружности и луча ОС буквой D.
ОD
Шаг 1. Построить окружность с центром О радиусом АВ.
Построение
отрезка, равного данному.
Слайд 16
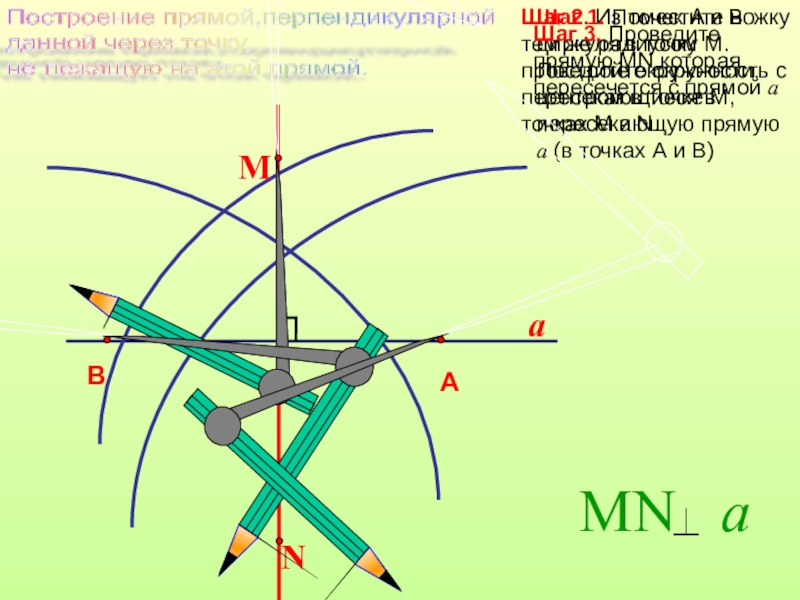
Дано: прямая a ,
Построить:
РМ а
М a
a
М
Вернемся к задаче
Слайд 17Шаг 2. Из точек А и В тем же радиусом проведите
Шаг 1. Поместите ножку циркуля в точку М. Постройте окружность с центром в точке М, пересекающую прямую а (в точках А и В)
Построение прямой,перпендикулярной
данной через точку,
не лежащую на этой прямой.
Шаг 3. Проведите прямую МN,которая пересечется с прямой а
a
N
М
А
В
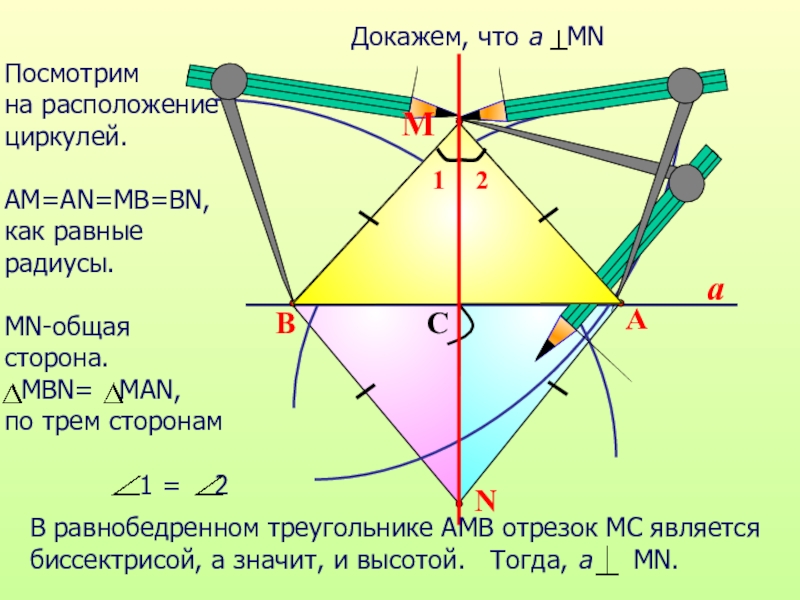
Слайд 18
a
N
B
A
C
М
Посмотрим
на расположение
циркулей.
АМ=АN=MB=BN,
как равные радиусы.
МN-общая сторона.
MВN=
по трем сторонам
Слайд 20
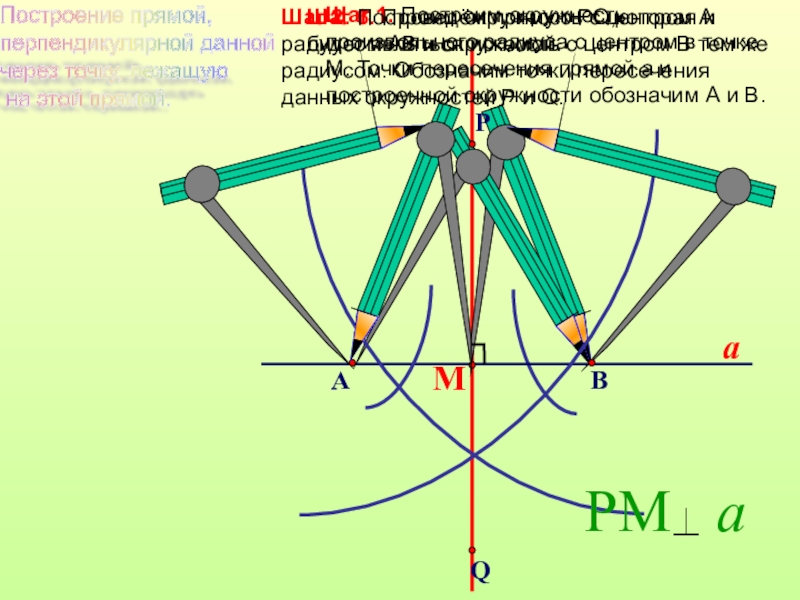
Дано:
прямая a ,
Построить: РМ а
М a
a
М
Рассмотрим задачу №3.
Слайд 21
М
a
Шаг 3. Проведём прямую PQ,которая и будет являться искомой.
Шаг 1. Построим
Шаг 2. Построим окружность с центром А радиусом АВ и окружность с центром В тем же радиусом. Обозначим точки пересечения данных окружностей P и Q.
Построение прямой,
перпендикулярной данной
через точку, лежащую
на этой прямой.
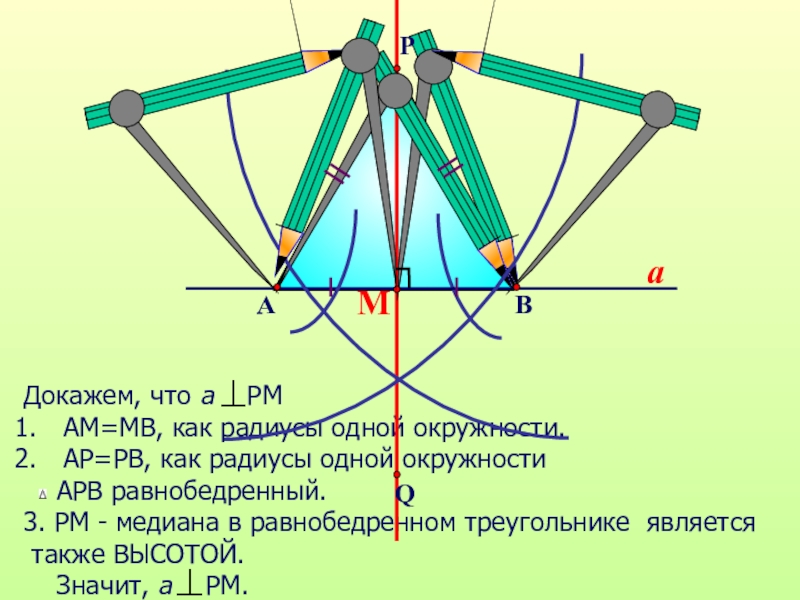
Слайд 22Докажем, что а РМ
АМ=МВ, как радиусы одной окружности.
АР=РВ, как радиусы
АРВ равнобедренный.
3. РМ - медиана в равнобедренном треугольнике является
также ВЫСОТОЙ.
Значит, а РМ.
М
a