«СОШ№3» город Валуйки
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Высоты, медианы и биссектрисы треугольника
Содержание
- 1. Презентация по геометрии на тему Высоты, медианы и биссектрисы треугольника
- 2. Цели урока: Образовательные: познакомить учащихся с
- 3. Развивающие:развитие мыслительных навыков, необходимых не только в
- 4. Воспитательные: воспитание настойчивости, целеустремленности, умения доводить начатое дело до логического завершения;
- 5. Повторение.Ответьте на вопрос: Какие геометрические фигуры вы знаете?Что такое треугольник? Сколько элементов имеет треугольник? Назовите их.
- 6. ВысотаВысота похожа на кота.Который, выгнув спинуИ под прямым угломСоединит вершинуИ сторону хвостом.
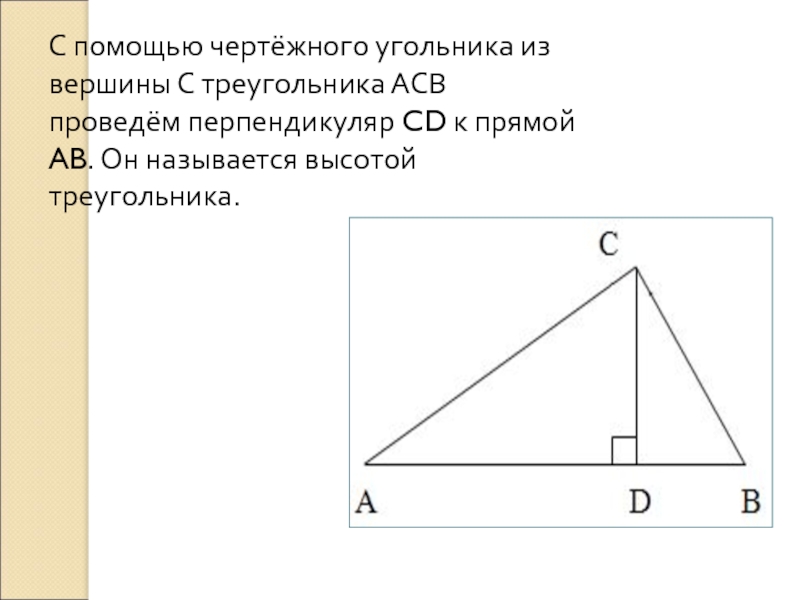
- 7. С помощью чертёжного угольника из вершины С
- 8. Высота треугольникаВысотой треугольника, опущенной из данной вершины
- 9. Вспомните определение биссектрисы угла.(Луч, исходящий из вершины
- 10. БиссектрисаБиссектриса - это крыса.Которая бегает по угламИ делит угол пополам.
- 11. Биссектриса треугольникаБиссектрисой треугольника, проведённой из данной вершины,
- 12. МедианаМедиана – обезьяна,У которой зоркий глаз.Прыгнет точно в серединуСтороны против вершины,Где находится сейчас.
- 13. 1.Начертите треугольник АBС и найдите середину отрезка
- 14. Медиана треугольникаМедианой треугольника, проведённой из данной вершины
- 15. Самостоятельно!Построить:1 вариант: все высоты в произвольном треугольнике.2
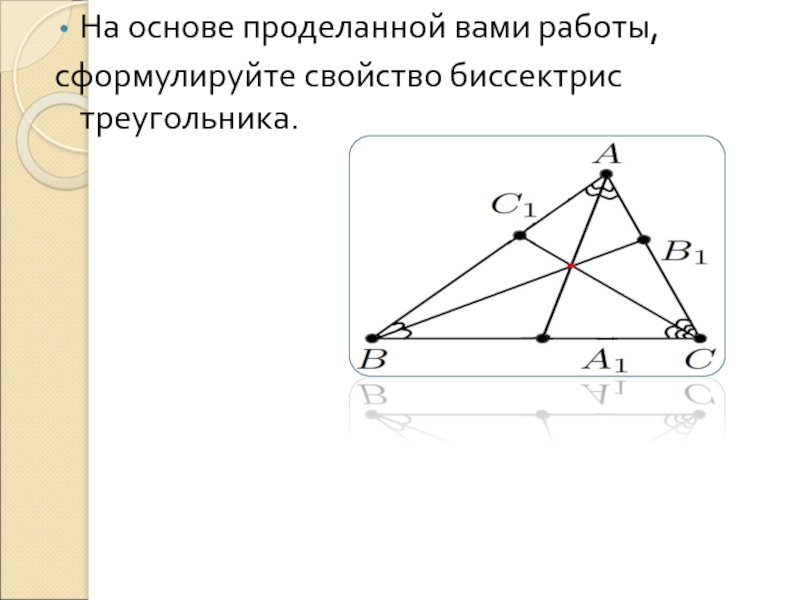
- 16. На основе проделанной вами работы,сформулируйте свойство биссектрис треугольника.
- 17. А сейчас подведём итог самостоятельной работы по
- 18. СПАСИБО ЗА УРОК! Удачи!
Цели урока: Образовательные: познакомить учащихся с новыми терминами : «высота, биссектриса, медиана» в треугольнике;научить распознавать на готовых чертежах высоту, медиану и биссектрису;научить самостоятельно строить в любом треугольнике высоты, биссектрисы , медианы; на основе полученных знаний,
Слайд 1Высоты, биссектрисы и медианы треугольника.
7 класс
Копаева Людмила Ивановна,
учитель математики
МОУ
Слайд 2Цели урока:
Образовательные:
познакомить учащихся с новыми терминами : «высота, биссектриса, медиана»
в треугольнике;
научить распознавать на готовых чертежах высоту, медиану и биссектрису;
научить самостоятельно строить в любом треугольнике высоты, биссектрисы , медианы;
на основе полученных знаний, сформулировать
свойство высот, биссектрис и медиан в треугольнике.
научить распознавать на готовых чертежах высоту, медиану и биссектрису;
научить самостоятельно строить в любом треугольнике высоты, биссектрисы , медианы;
на основе полученных знаний, сформулировать
свойство высот, биссектрис и медиан в треугольнике.
Слайд 3Развивающие:
развитие мыслительных навыков, необходимых не только в учебе, но и в
обычной жизни:
умение работать с информацией,
анализировать различные стороны явлений, осмысливать ситуацию;
умение аргументировать принятое решение.
умение работать с информацией,
анализировать различные стороны явлений, осмысливать ситуацию;
умение аргументировать принятое решение.
Слайд 4Воспитательные:
воспитание настойчивости, целеустремленности, умения доводить начатое дело до логического завершения;
Слайд 5Повторение.
Ответьте на вопрос: Какие геометрические фигуры вы знаете?
Что такое треугольник?
Сколько
элементов имеет треугольник? Назовите их.
Слайд 6Высота
Высота похожа на кота.
Который, выгнув спину
И под прямым углом
Соединит вершину
И сторону
хвостом.
Слайд 7С помощью чертёжного угольника из вершины С треугольника АСВ проведём перпендикуляр
CD к прямой AB. Он называется высотой треугольника.
Слайд 8Высота треугольника
Высотой треугольника, опущенной из данной вершины , называется перпендикуляр, проведённый
из этой вершины к прямой, которая содержит противолежащую сторону треугольника.
А
А
С
В
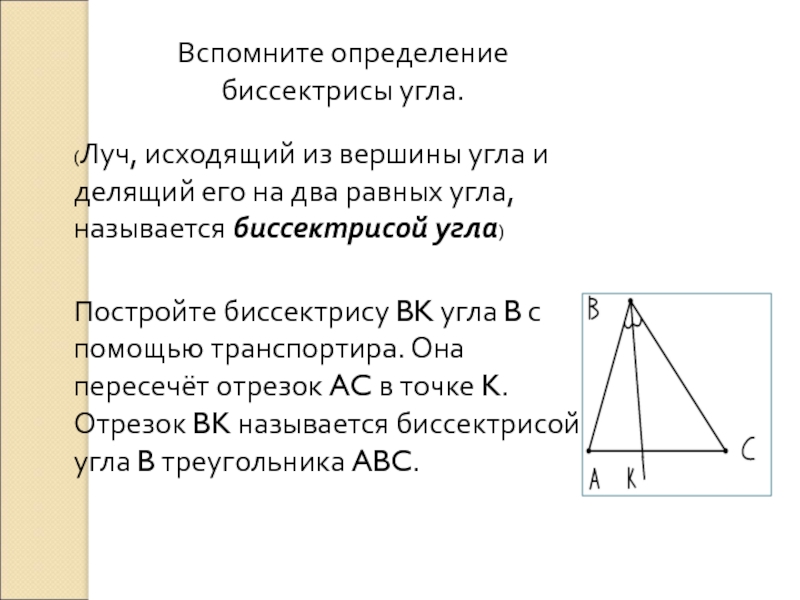
Слайд 9Вспомните определение биссектрисы угла.
(Луч, исходящий из вершины угла и делящий его
на два равных угла, называется биссектрисой угла)
Постройте биссектрису BK угла B с помощью транспортира. Она пересечёт отрезок AC в точке K. Отрезок BK называется биссектрисой угла B треугольника ABC.
Слайд 11Биссектриса треугольника
Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла
треугольника, соединяющий эту вершину с точкой на противолежащей стороне.
В
А С
В
А С
Слайд 12Медиана
Медиана – обезьяна,
У которой зоркий глаз.
Прыгнет точно в середину
Стороны против вершины,
Где
находится сейчас.
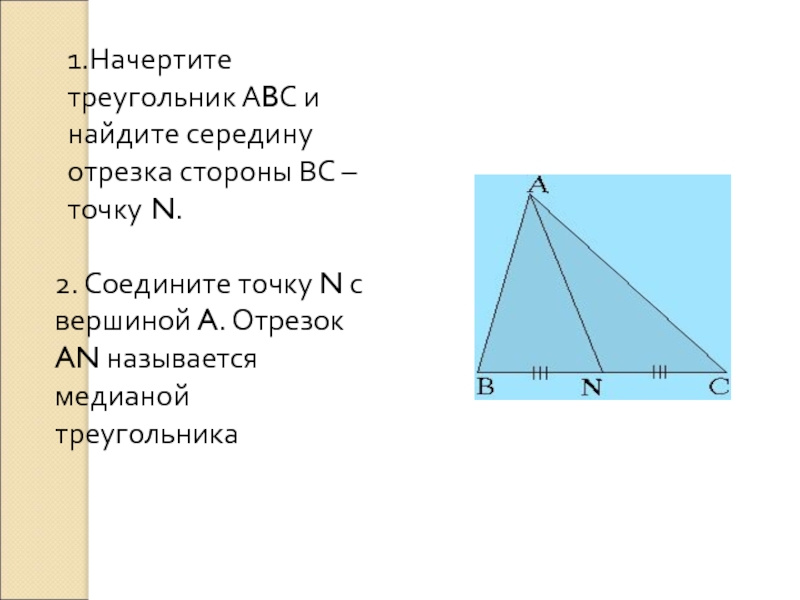
Слайд 131.Начертите треугольник АBС и найдите середину отрезка стороны ВС – точку
N.
2. Соедините точку N с вершиной A. Отрезок AN называется медианой треугольника
Слайд 14Медиана треугольника
Медианой треугольника, проведённой из данной вершины , называется отрезок ,
соединяющий эту вершину с серединой противолежащей стороны треугольника.
А
В
С
Слайд 15Самостоятельно!
Построить:
1 вариант: все высоты в произвольном треугольнике.
2 вариант: все медианы в
произвольном треугольнике.
3 вариант: все биссектрисы в произвольном треугольнике.
3 вариант: все биссектрисы в произвольном треугольнике.
Слайд 17
А сейчас подведём итог самостоятельной работы по новой теме.
При
выполнении практической работы получили следующие результаты:
1. В любом треугольнике биссектрисы пересекаются в одной точке.
1. В любом треугольнике биссектрисы пересекаются в одной точке.
3. В любом треугольнике медианы пересекаются в одной точке.
2. В любом треугольнике высоты
пересекаются в одной точке.
