Чему бы ты ни учился,
ты учишься для себя.
(Петроний- сатирик Древней Греции)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Внешний угол треугольника, 7 класс
Содержание
- 1. Презентация по геометрии на тему: Внешний угол треугольника, 7 класс
- 2. Приветствую вас на уроке геометрии в 7 классе Урок №42
- 3. Успешного усвоения нового материала
- 4. Проверка Д.Р № 39 на 18.02.16Глава 4,§1,
- 5. Дано: ∆ АВС – равнобедренный,
- 6. Дано: ∆ АВС – равнобедренный,
- 7. Слайд 7
- 8. Слайд 8
- 9. Экспресс- опрос
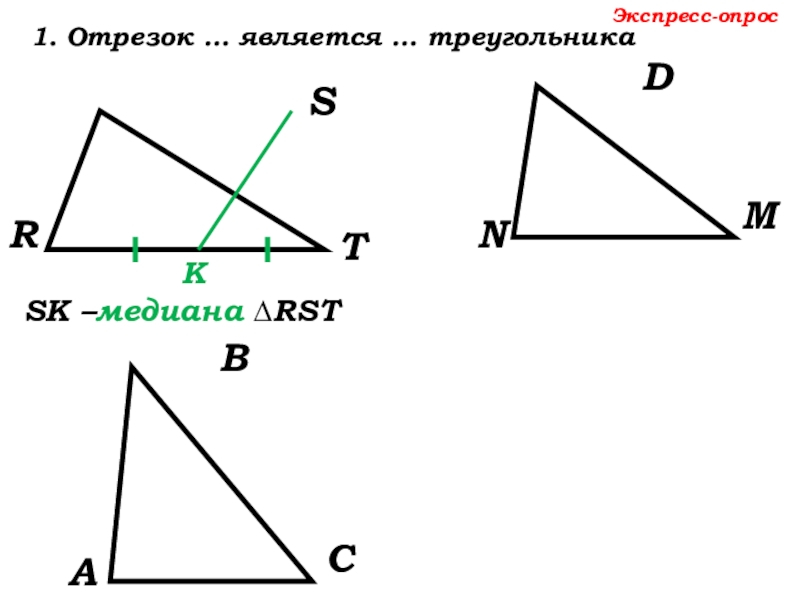
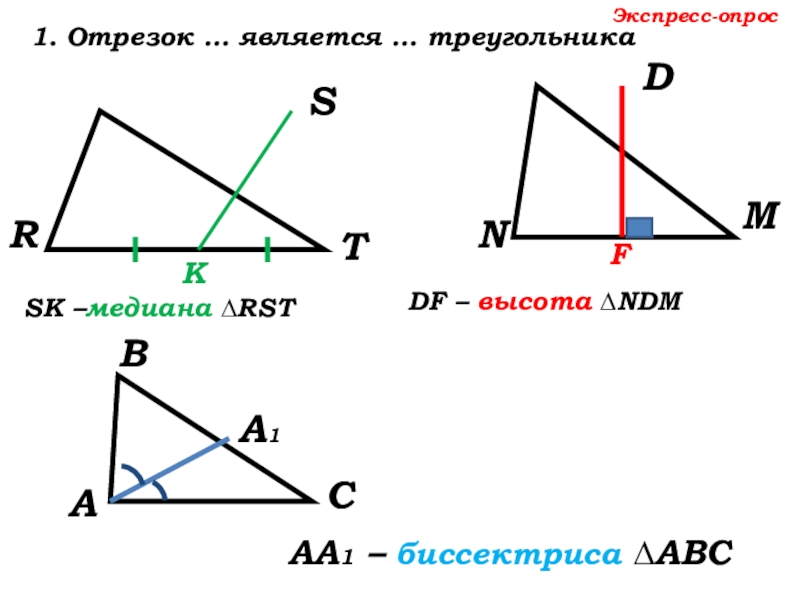
- 10. DNMRSTSК –Экспресс-опрос1. Отрезок … является … треугольникаК
- 11. DNMRSTSК –медиана ∆RST Экспресс-опрос1. Отрезок … является … треугольникаК
- 12. DNMRSTSК –медиана ∆RST Экспресс-опрос1. Отрезок … является
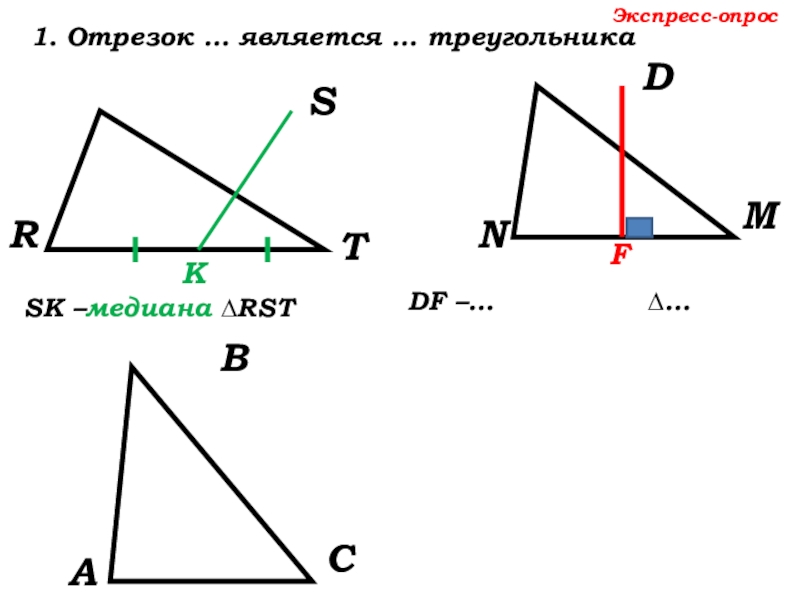
- 13. DNMRSTSК –медиана ∆RST Экспресс-опрос1. Отрезок … является … треугольникаКDF – высота ∆NDM F
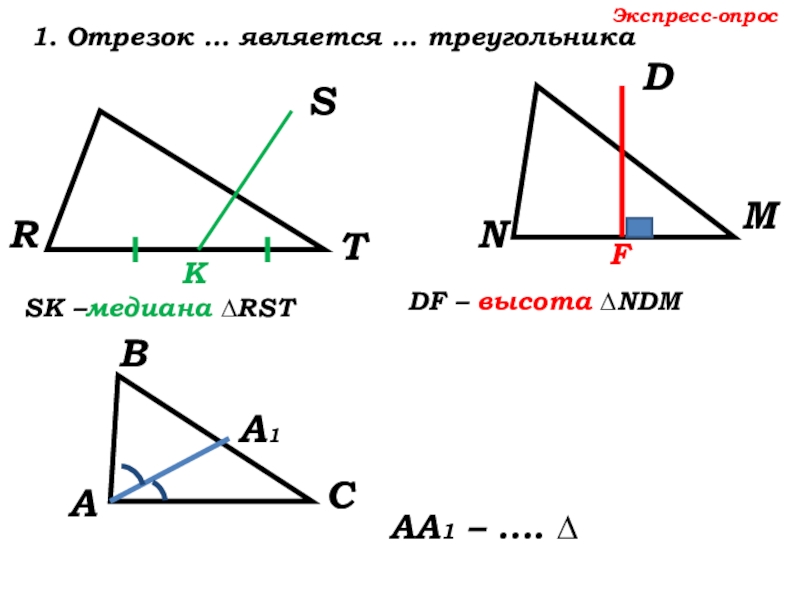
- 14. DNMRSTSК –медиана ∆RST Экспресс-опрос1. Отрезок … является … треугольникаКDF – высота ∆NDM FАА1 – …. ∆
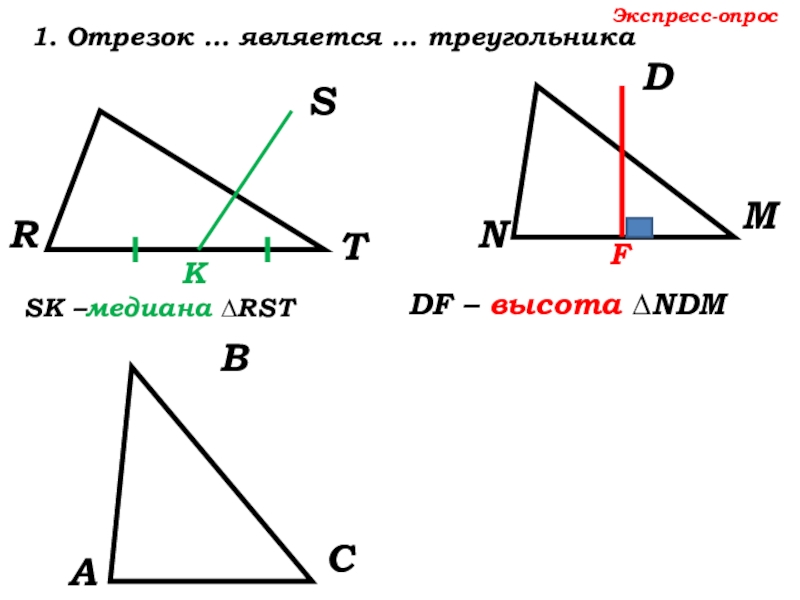
- 15. DNMRSTSК –медиана ∆RST Экспресс-опрос1. Отрезок … является … треугольникаКDF – высота ∆NDM FАА1 – биссектриса ∆АВС
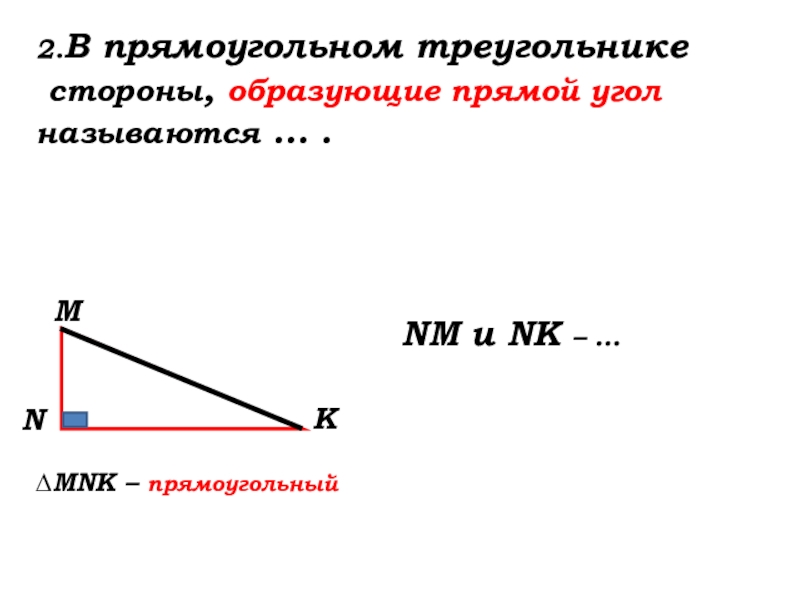
- 16. ∆MNK – прямоугольный2.В прямоугольном треугольнике стороны, образующие
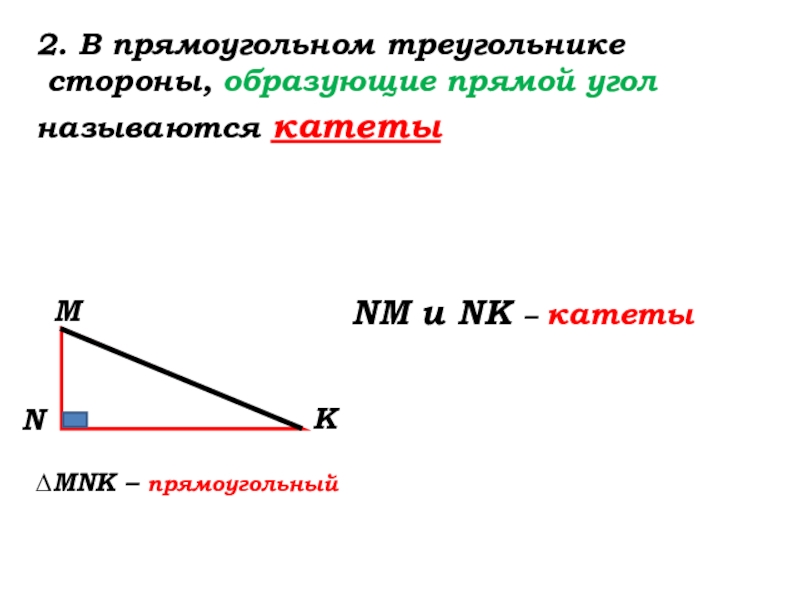
- 17. ∆MNK – прямоугольный2. В прямоугольном треугольнике стороны,
- 18. ∆MNK – прямоугольный2.В прямоугольном треугольнике сторона,
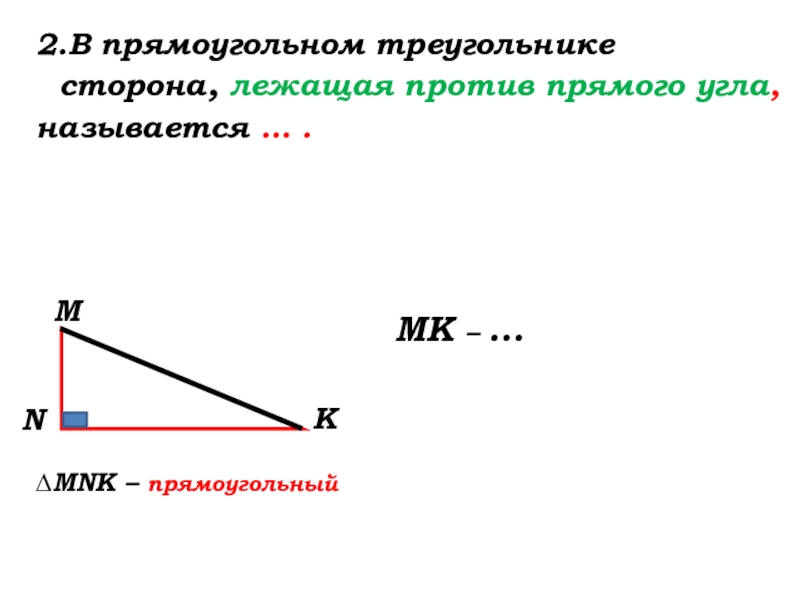
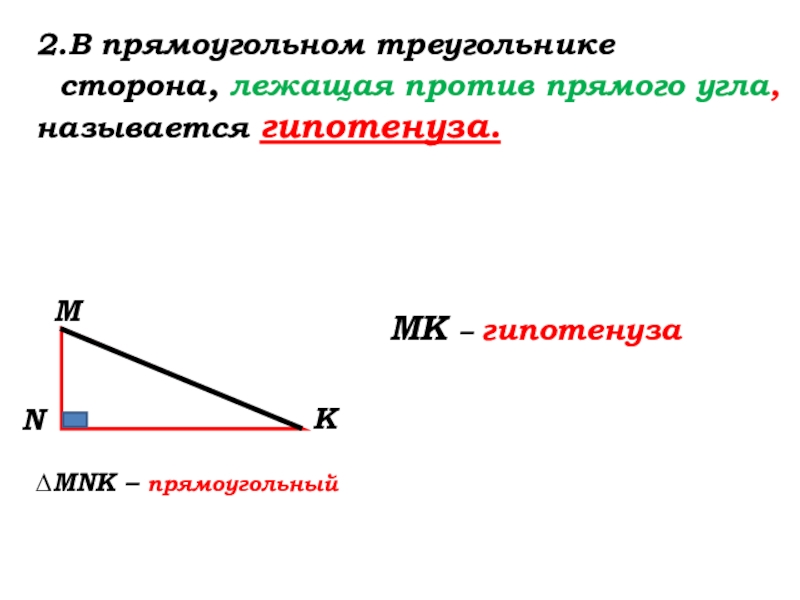
- 19. ∆MNK – прямоугольный2.В прямоугольном треугольнике сторона, лежащая против прямого угла,называется гипотенуза. МК – гипотенуза
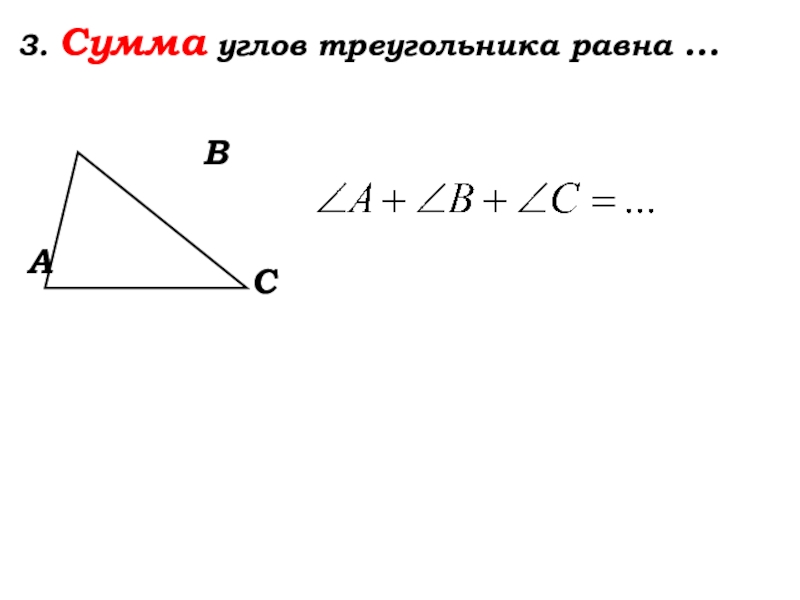
- 20. 3. Сумма углов треугольника равна … АВС
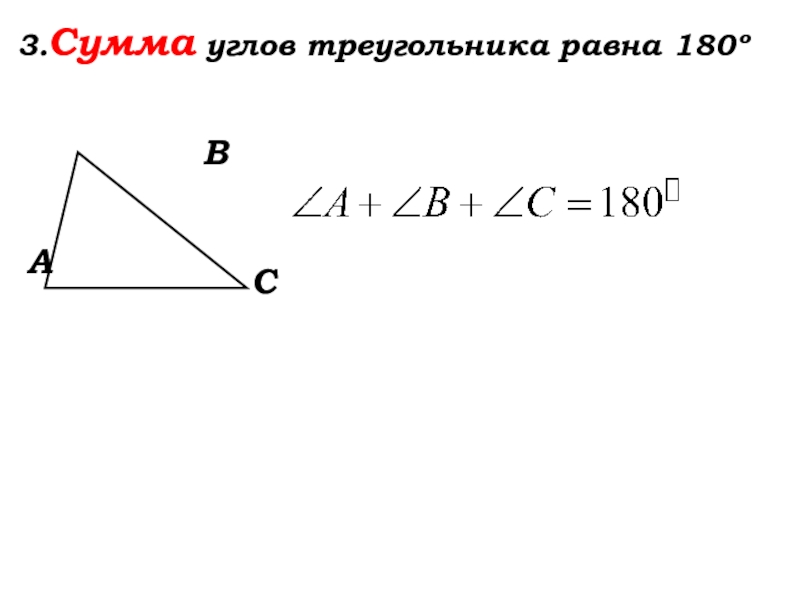
- 21. 3.Сумма углов треугольника равна 180º АВС
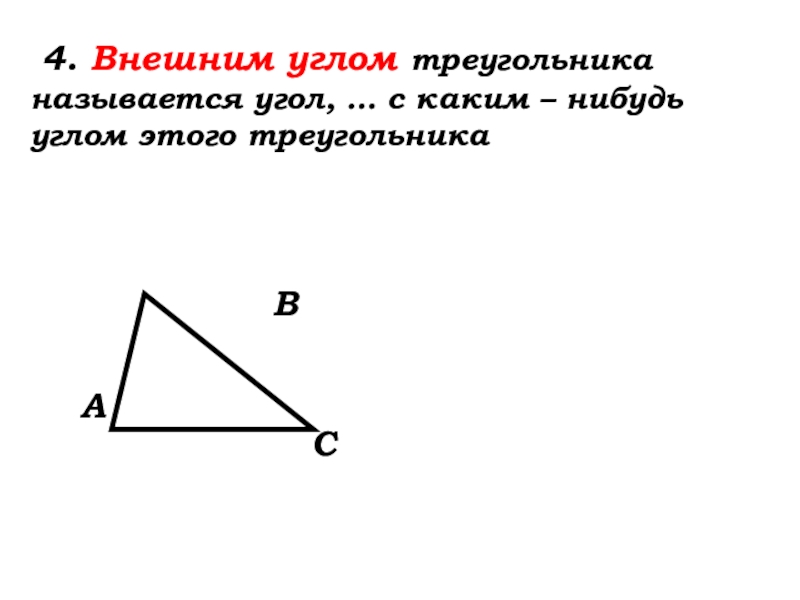
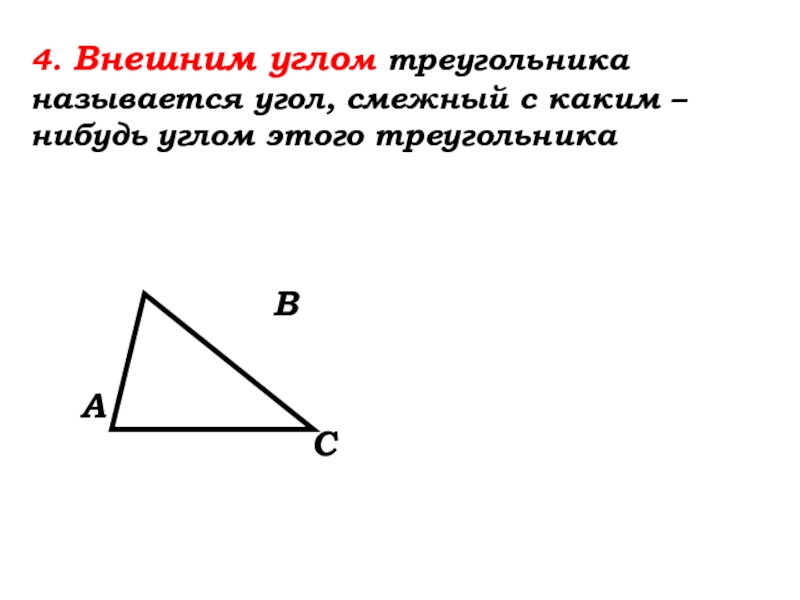
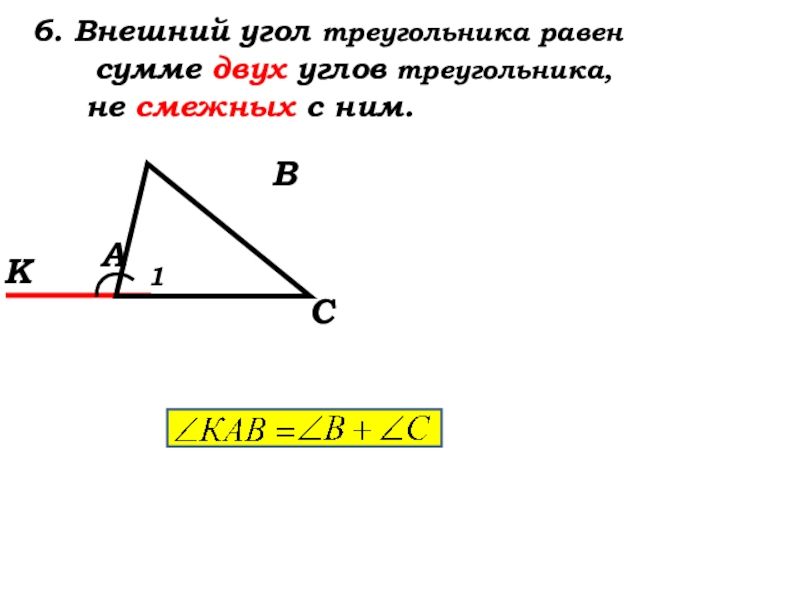
- 22. 4. Внешним углом
- 23. 4. Внешним углом
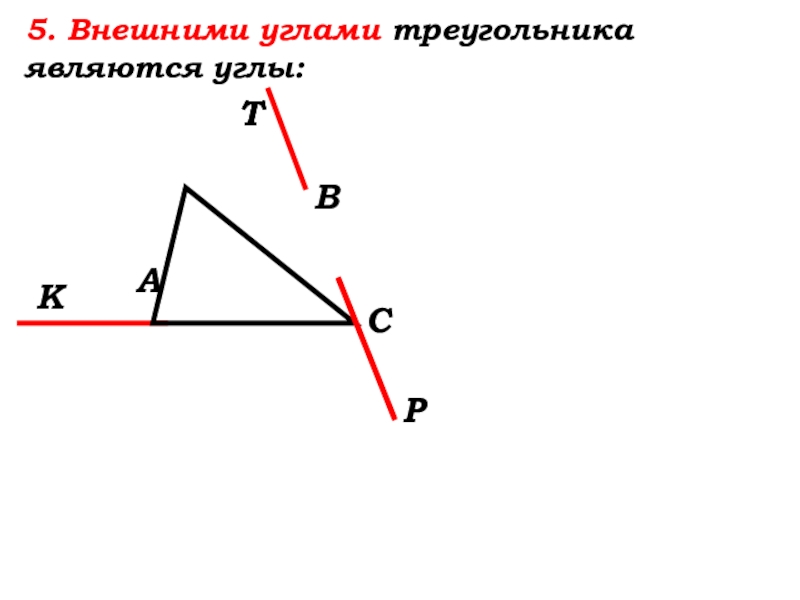
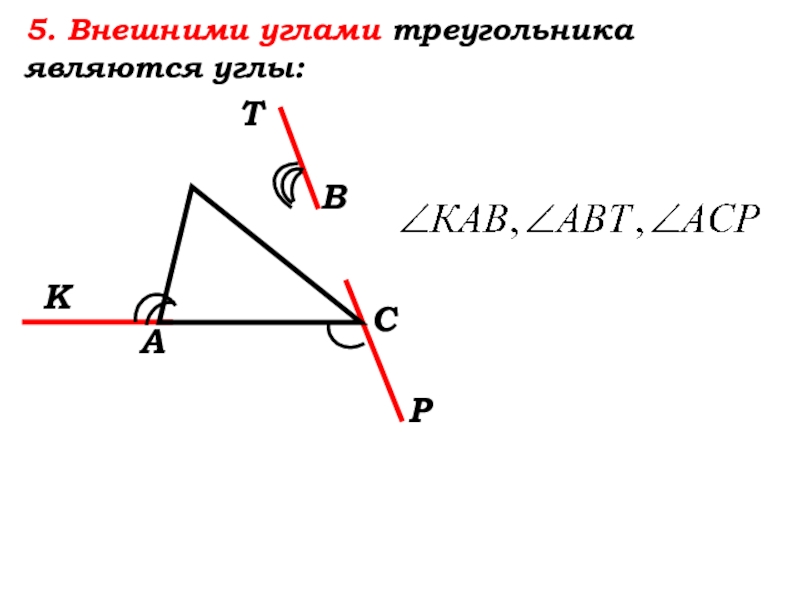
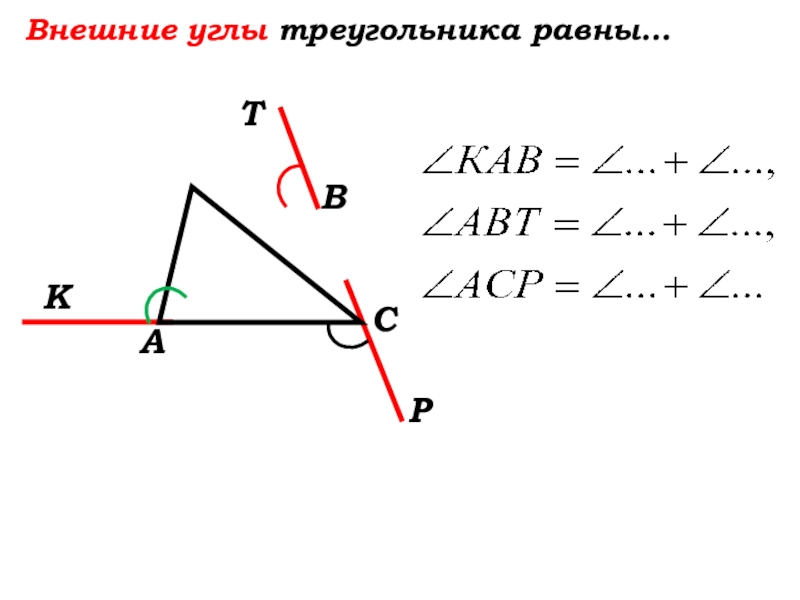
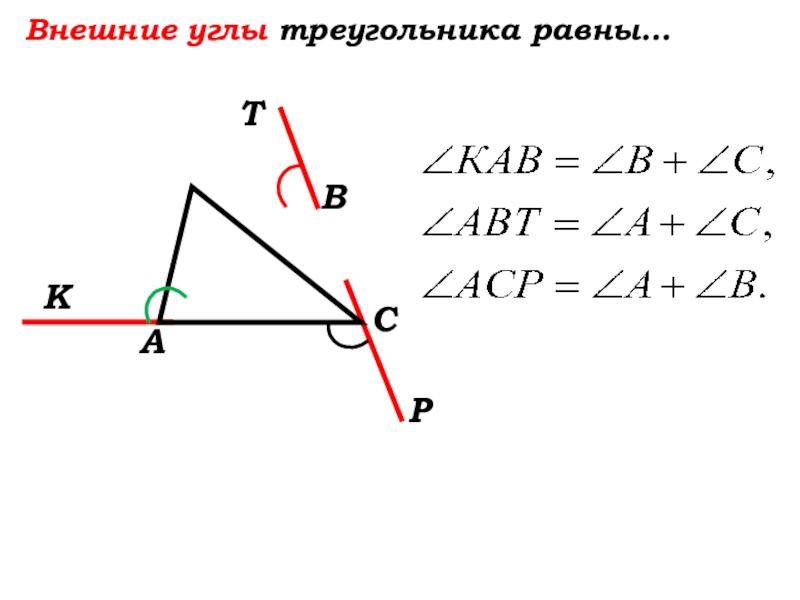
- 24. 5. Внешними углами треугольника являются углы:
- 25. 5. Внешними углами треугольника являются углы:Т
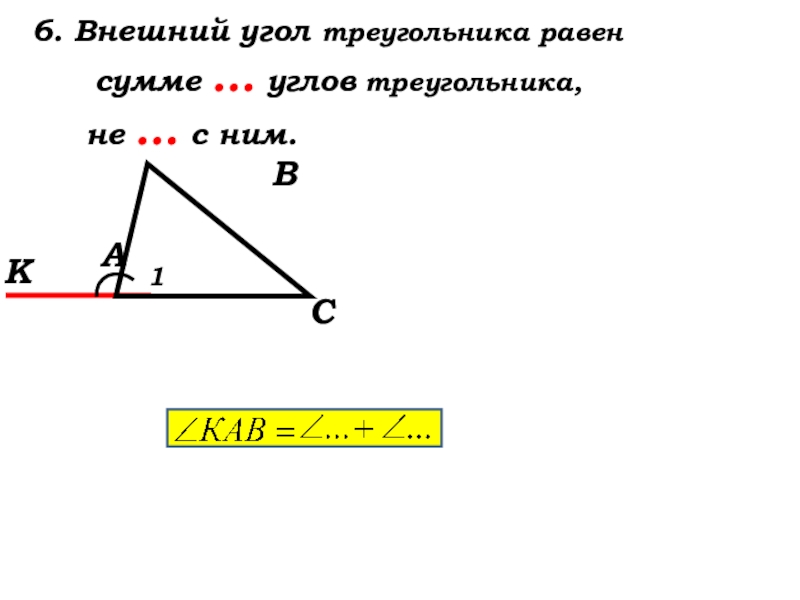
- 26. 6. Внешний угол
- 27. 6. Внешний угол
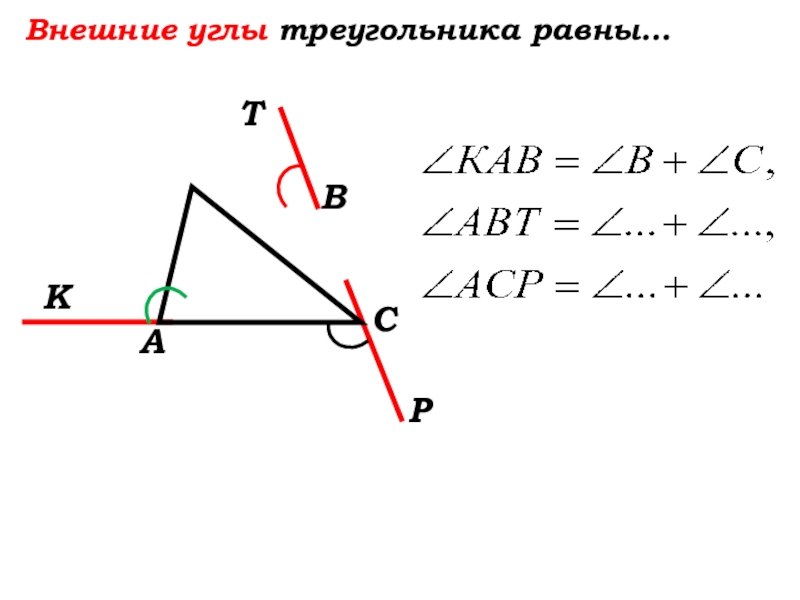
- 28. Внешние углы треугольника равны…Т
- 29. Внешние углы треугольника равны…Т
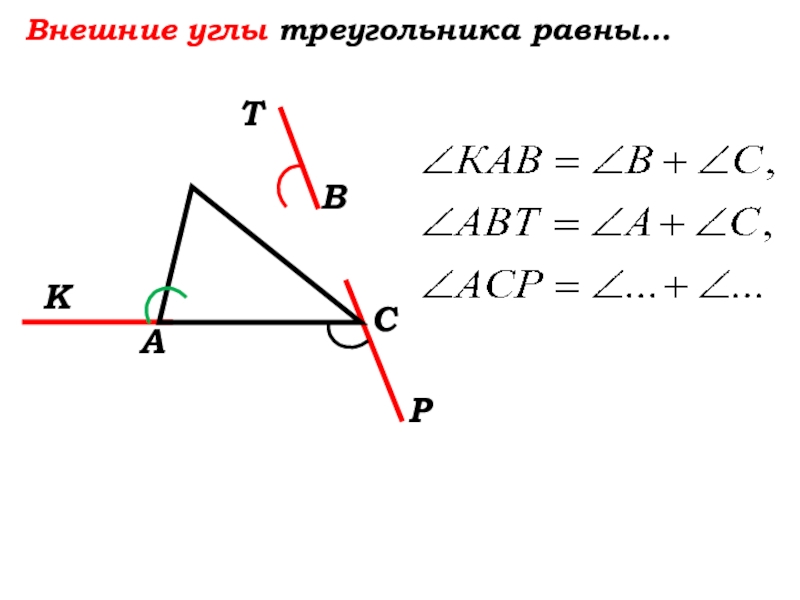
- 30. Внешние углы треугольника равны…Т
- 31. Внешние углы треугольника равны…Т
- 32. Сумма углов треугольника.Внешний угол треугольникап.п.30 – 3118.02.2016г.К.Р.
- 33. Цели урока:Учиться решать задачи на применение теоремы
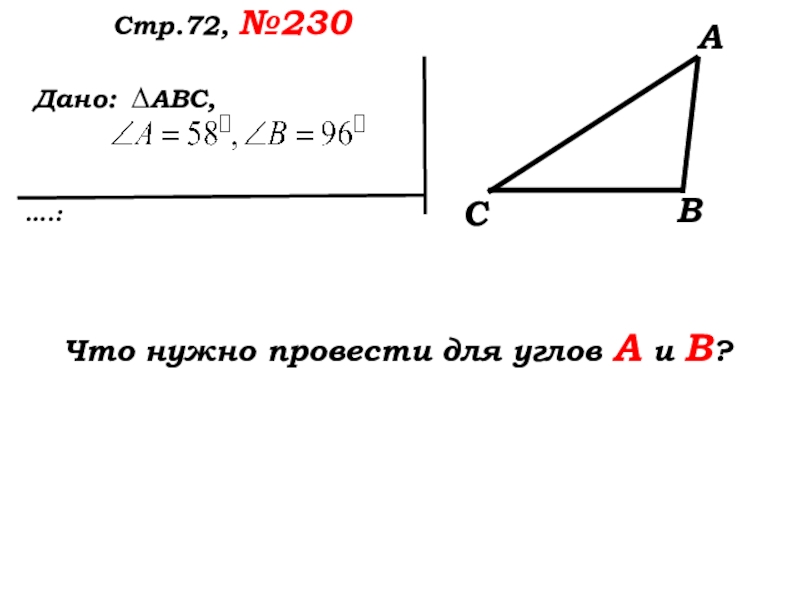
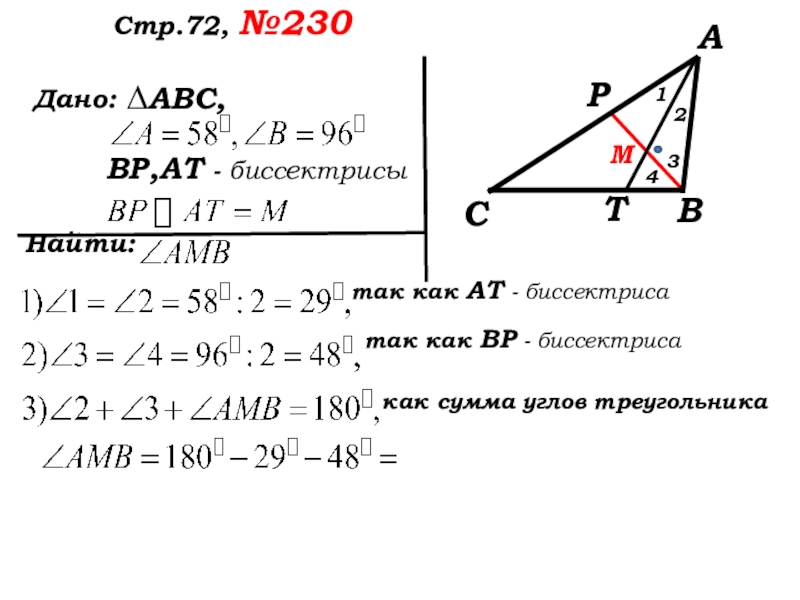
- 34. Стр.72, №230Какой треугольник дан в задаче?Что известно
- 35. Дано: ….:Стр.72, №230 ∆АВС,Какой треугольник АВС чертим?
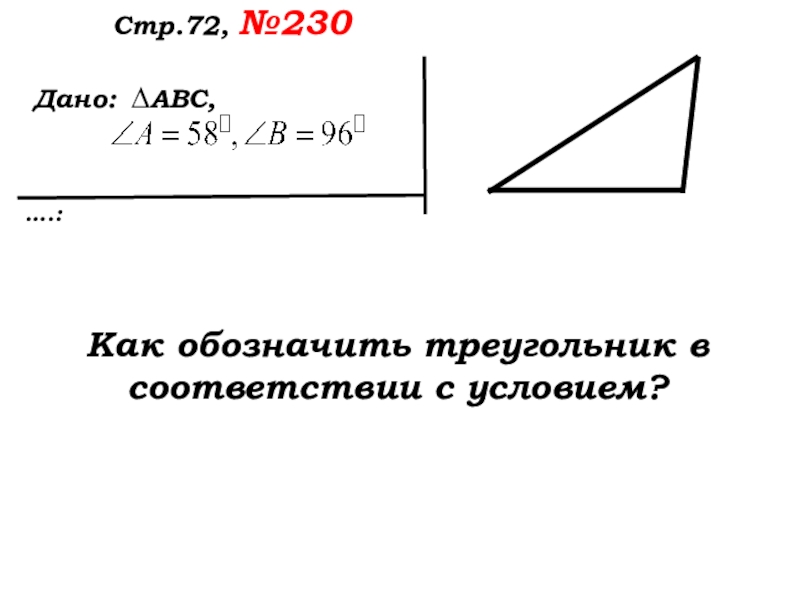
- 36. Дано: ….:Стр.72, №230 ∆АВС,Как обозначить треугольник в соответствии с условием?
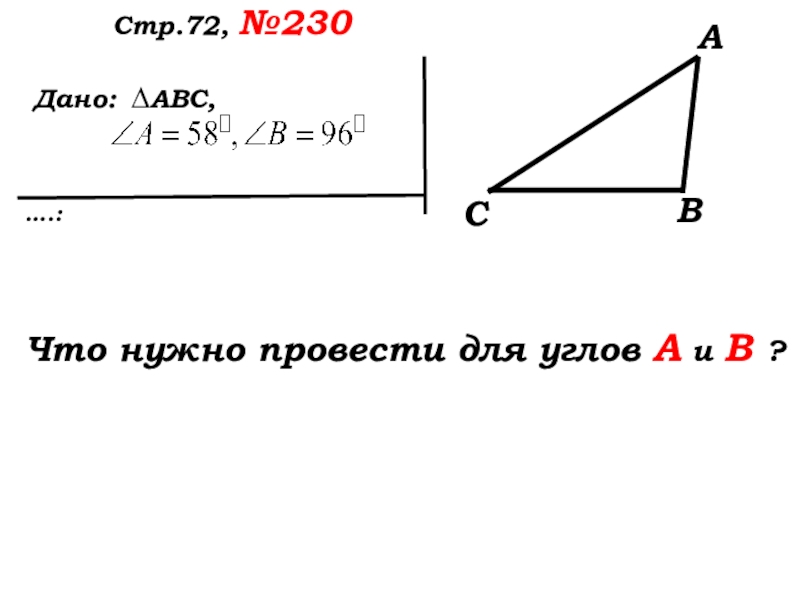
- 37. Дано: ….:Стр.72, №230 ∆АВС,Что нужно провести для углов А и В ?АВС
- 38. Дано: ….:Стр.72, №230 ∆АВС,Что нужно провести для углов А и В?АВС
- 39. Дано: ….:Стр.72, №230
- 40. Дано: ….:Стр.72, №230
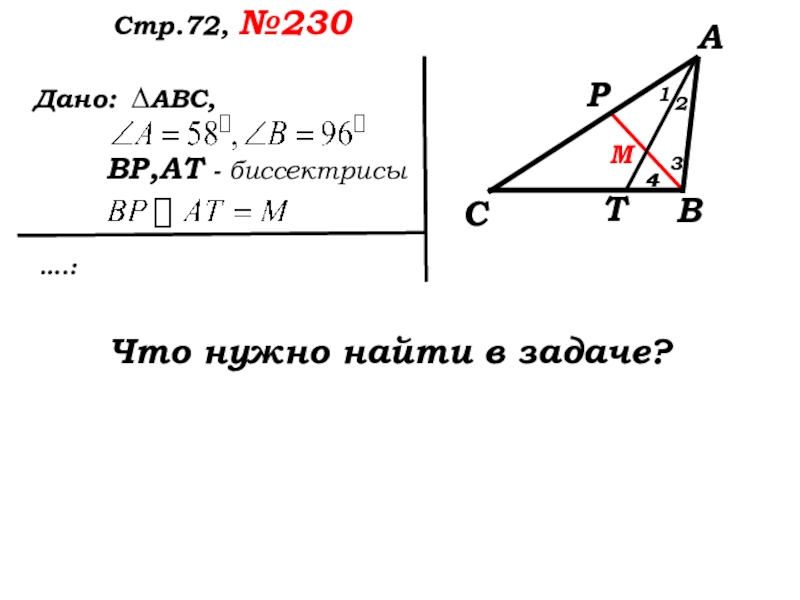
- 41. Дано: ….:Стр.72, №230 ∆АВС,ВР,АТ - биссектрисы12344Что нужно найти в задаче?
- 42. Дано: Найти:Стр.72, №230
- 43. Дано: Найти:Стр.72, №230 ∆АВС,ВР,АТ - биссектрисы3124так как АТ - биссектриса
- 44. Дано: Найти:Стр.72, №230
- 45. Дано: Найти:Стр.72, №230
- 46. Дано: Найти:Стр.72, №230
- 47. Дано: Найти:Стр.72, №230
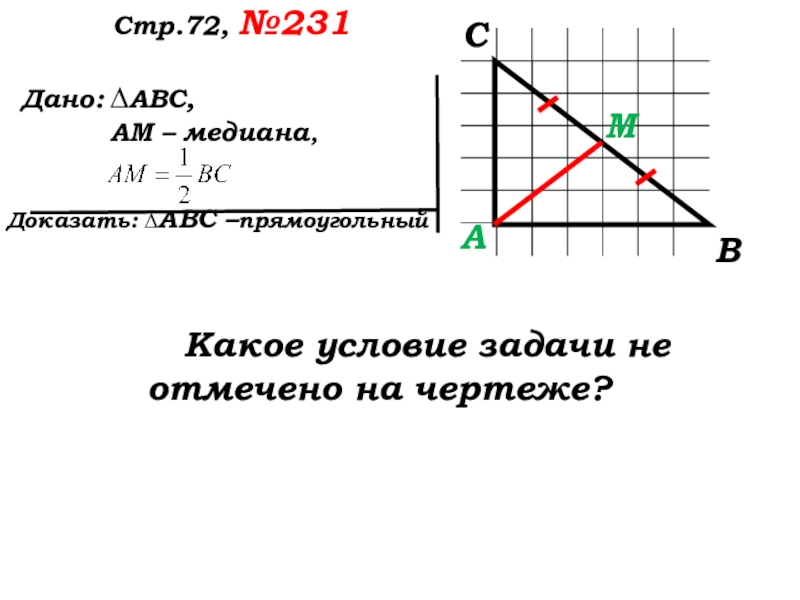
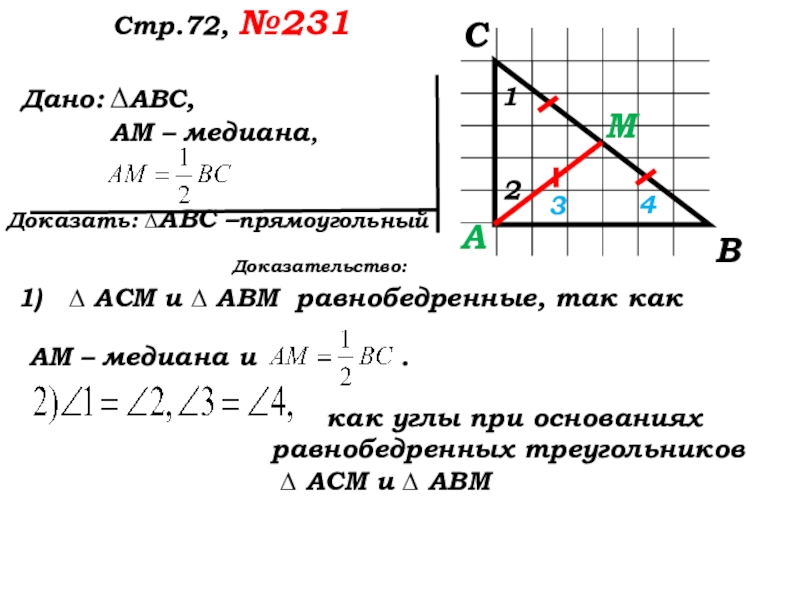
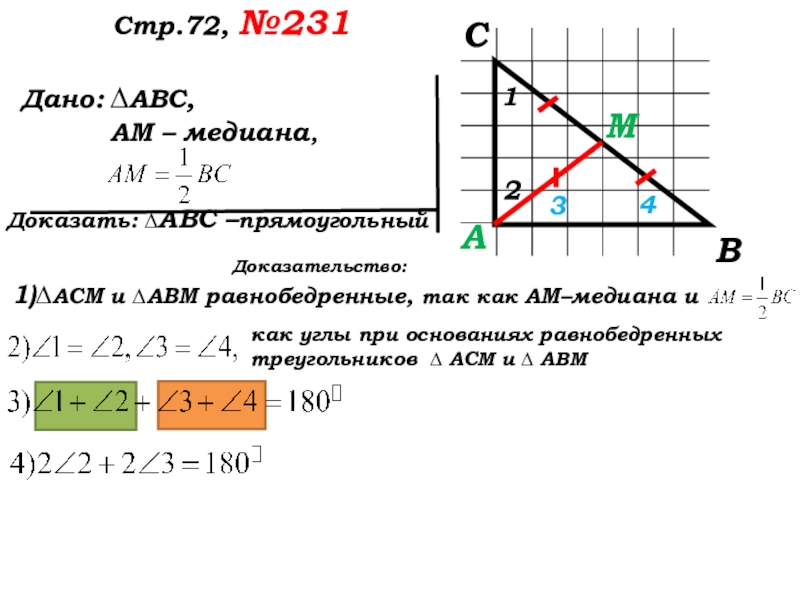
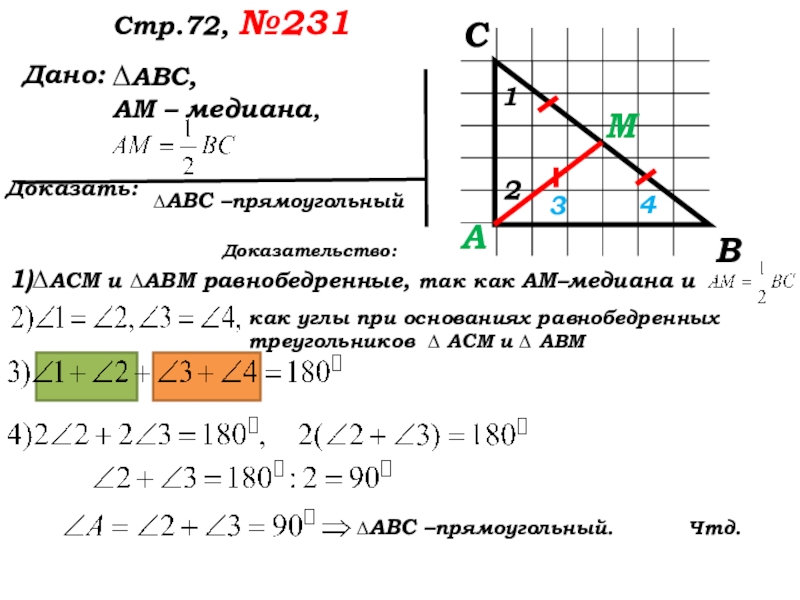
- 48. Стр.72, №231Прочитайте задачу?Что известно в треугольнике?Что нужно доказать?Какой треугольник дан в задаче?Какой следует выполнить чертёж?
- 49. Дано: Доказать: ∆АВС –прямоугольный Стр.72, №231 ∆АВС,АМ – медиана,Какой треугольник АВС чертим?
- 50. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 51. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 52. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 53. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 54. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 55. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 56. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 57. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 58. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 59. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 60. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 61. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 62. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 63. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 64. Дано: Доказать: ∆АВС –прямоугольный Стр.72,
- 65. Дано: Доказать: Стр.72, №231
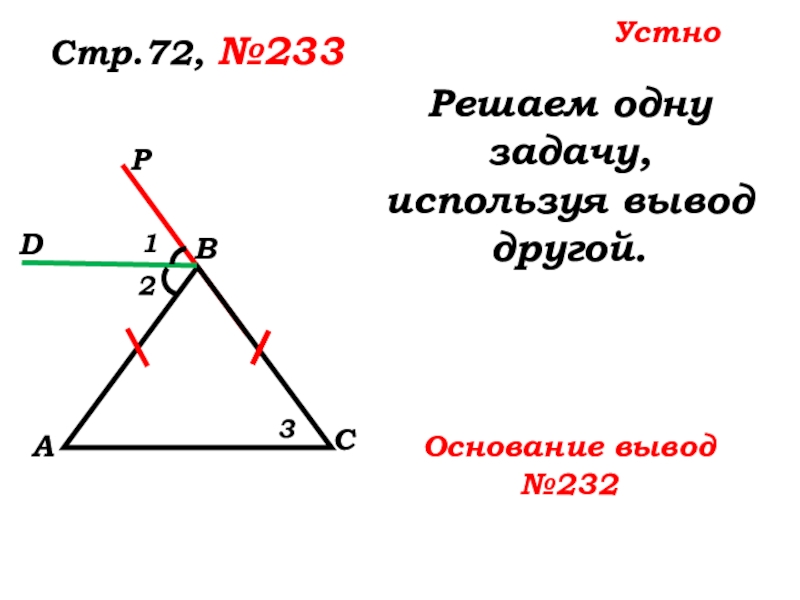
- 66. Решаем одну задачу, используя вывод другой.Стр.72, №233 123DУстноОснование вывод №232
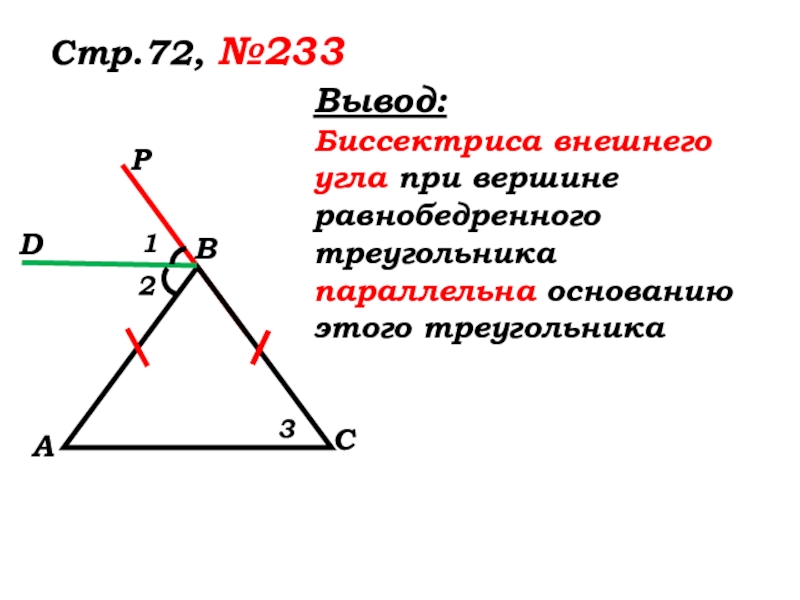
- 67. Вывод:Биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию этого треугольникаСтр.72, №233 123
- 68. Итоги урока
- 69. Оценки за урок
- 70. Д.Р № 39 Глава 4,§1, пп.30-31Знать: теорему,
Приветствую вас на уроке геометрии в 7 классе Урок №42
Слайд 1 Урок геометрии в 7 классе. Автор разработки: учитель математики МБОУ СШ № 10
г. Павлово
Леонтьева Светлана Ивановна
Слайд 3
Успешного усвоения нового материала
Интересные мысли и высказывания
Доказательство –
это рассуждение,
которое убеждает.
Ю.А. Шиханович
Слайд 4
Проверка Д.Р № 39
на 18.02.16
Глава 4,§1, пп.30-31
Знать: теорему, опр. внешнего
угла, опр. видов треугольника
Записи в тетради
Стр.72, №227, 232
Записи в тетради
Стр.72, №227, 232
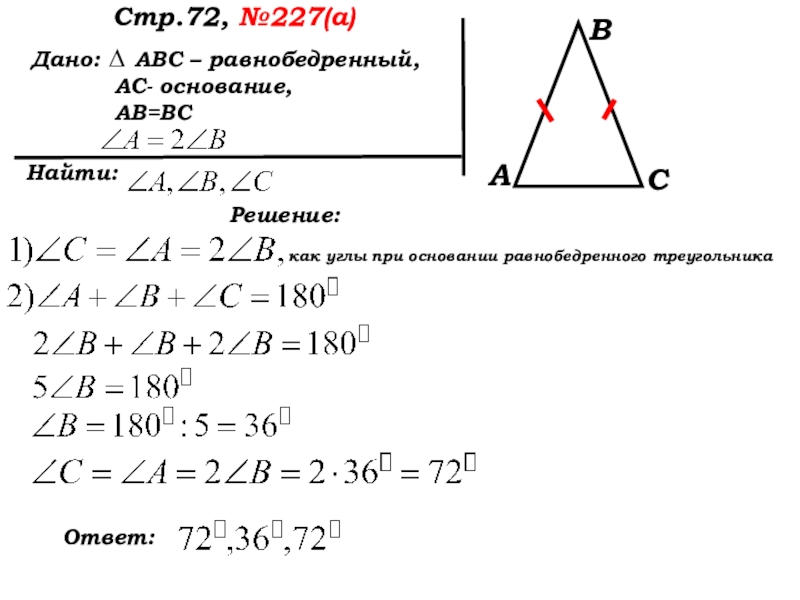
Слайд 5 Дано: ∆ АВС – равнобедренный,
АС- основание,
АВ=ВС
АВ=ВС
Найти:
Стр.72, №227(а)
Решение:
А
В
С
как углы при основании равнобедренного треугольника
Ответ:
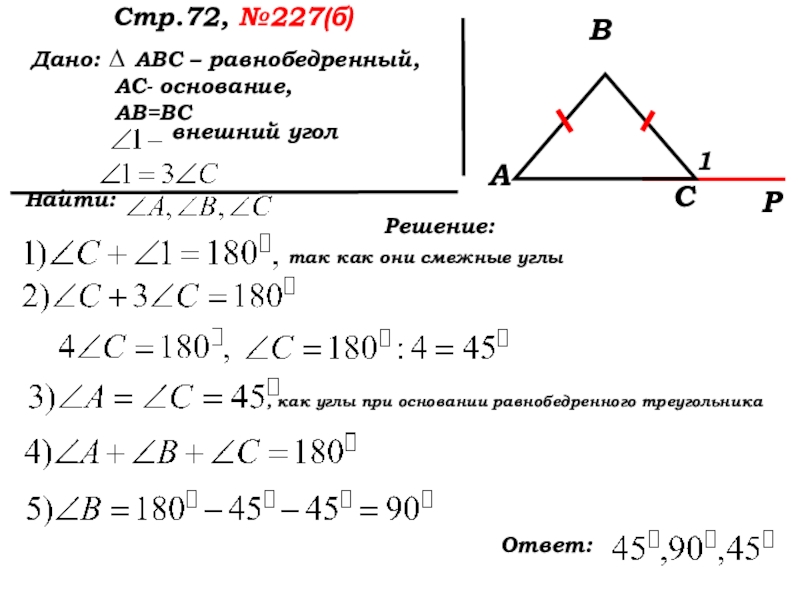
Слайд 6 Дано: ∆ АВС – равнобедренный,
АС- основание,
АВ=ВС
АВ=ВС
Найти:
Стр.72, №227(б)
Решение:
А
В
С
так как они смежные углы
Ответ:
Р
внешний угол
1
, как углы при основании равнобедренного треугольника
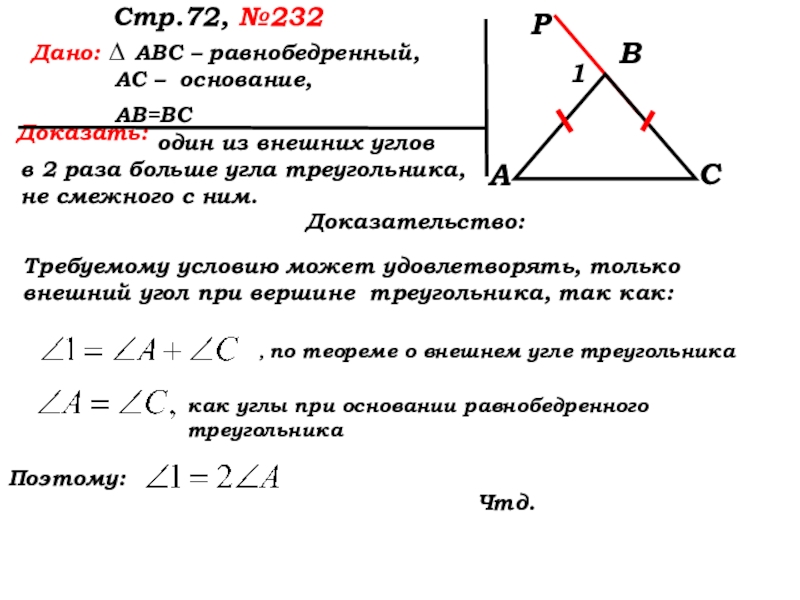
Слайд 7 один из
внешних углов
в 2 раза больше угла треугольника, не смежного с ним.
в 2 раза больше угла треугольника, не смежного с ним.
Дано: ∆ АВС – равнобедренный,
АС – основание,
АВ=ВС
Доказать:
Стр.72, №232
Доказательство:
Требуемому условию может удовлетворять, только внешний угол при вершине треугольника, так как:
Чтд.
, по теореме о внешнем угле треугольника
как углы при основании равнобедренного треугольника
Поэтому:
Слайд 8
Оцените ДР:
- все ответы верны и подробно записано решение «5»
- ответы в основном верны и записано решение, но допущены логические или вычислительные ошибки «4»
- ответы в основном верны, но решение либо неполное, либо его нет совсем «3»
- ответы не верны, в решении допущены существенные ошибки «2»
-домашняя работа отсутствует «1»
Слайд 13
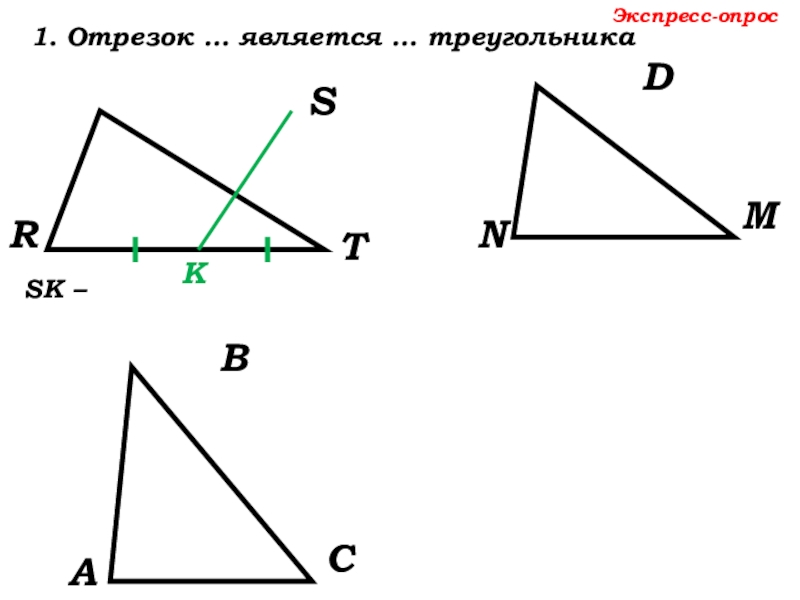
D
N
M
R
S
T
SК –медиана ∆RST
Экспресс-опрос
1. Отрезок … является … треугольника
К
DF – высота
∆NDM
F
Слайд 14
D
N
M
R
S
T
SК –медиана ∆RST
Экспресс-опрос
1. Отрезок … является … треугольника
К
DF – высота
∆NDM
F
АА1 – …. ∆
Слайд 15
D
N
M
R
S
T
SК –медиана ∆RST
Экспресс-опрос
1. Отрезок … является … треугольника
К
DF – высота
∆NDM
F
АА1 – биссектриса ∆АВС
Слайд 16∆MNK – прямоугольный
2.В прямоугольном треугольнике
стороны, образующие прямой угол называются
… .
NM и NK – …
Слайд 17∆MNK – прямоугольный
2. В прямоугольном треугольнике
стороны, образующие прямой угол
называются катеты
NM и NK – катеты
Слайд 18∆MNK – прямоугольный
2.В прямоугольном треугольнике
сторона, лежащая против прямого угла,
называется
… .
МК – …
Слайд 19∆MNK – прямоугольный
2.В прямоугольном треугольнике
сторона, лежащая против прямого угла,
называется
гипотенуза.
МК – гипотенуза
Слайд 23
4. Внешним углом треугольника называется угол, смежный
с каким – нибудь углом этого треугольника
Слайд 33Цели урока:
Учиться решать задачи на применение теоремы о сумме углов треугольника.
Учиться
решать задачи на применение теоремы о величине внешнего угла треугольника.
Формировать правильную математическую речь.
Формировать правильную математическую речь.
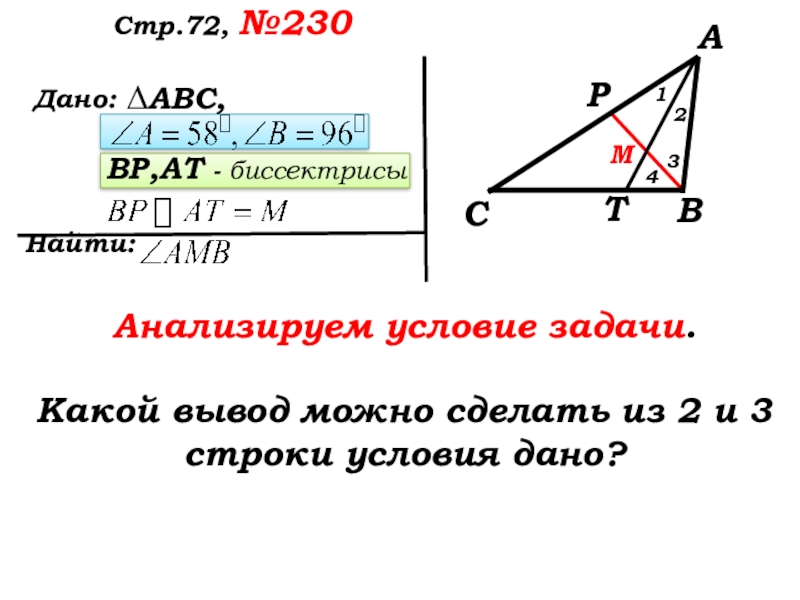
Слайд 34Стр.72, №230
Какой треугольник дан в задаче?
Что известно в треугольнике?
Какими являются углы
А и В?
Какие отрезки проведены
и какого их взаимное расположение?
Что записать в условие, какой треугольник начертить?
Слайд 39 Дано:
….:
Стр.72, №230
∆АВС,
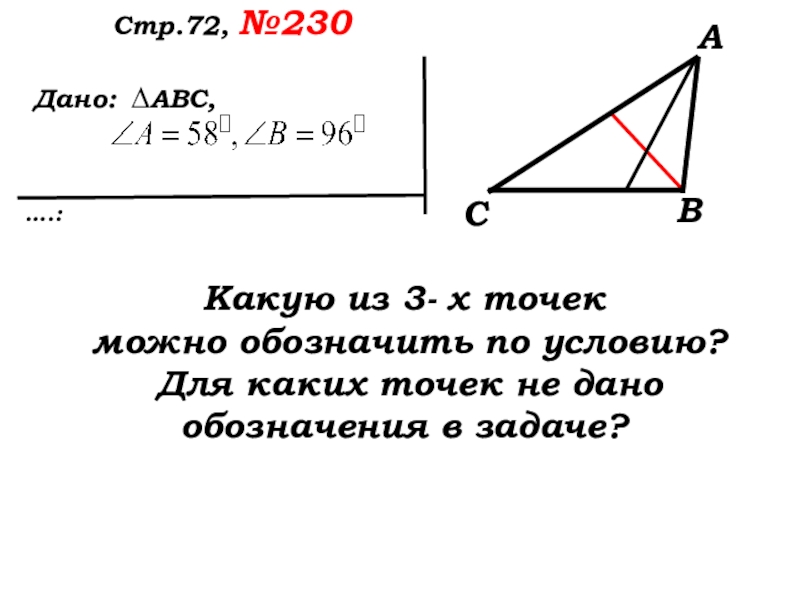
Какую из 3- х
точек
можно обозначить по условию?
Для каких точек не дано обозначения в задаче?
можно обозначить по условию?
Для каких точек не дано обозначения в задаче?
Слайд 40 Дано:
….:
Стр.72, №230
∆АВС,
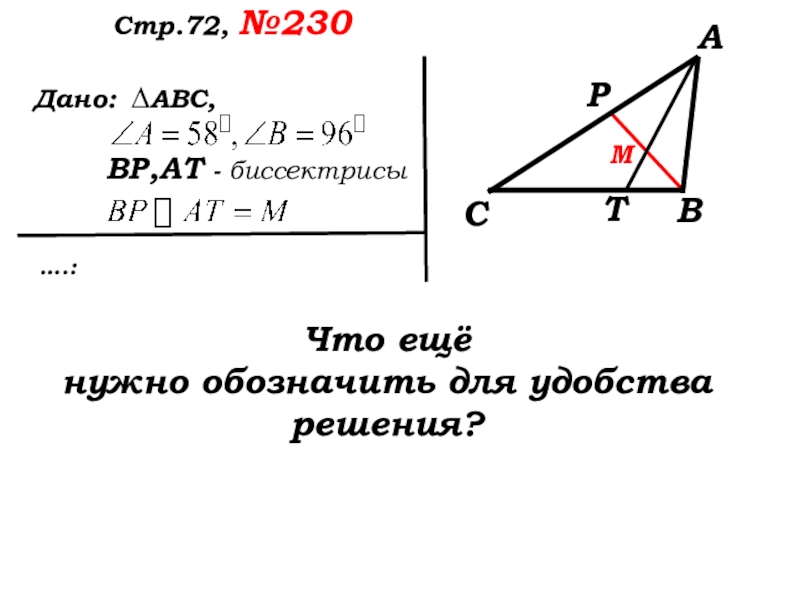
ВР,АТ - биссектрисы
Что ещё
нужно обозначить для удобства решения?
Слайд 42
Дано:
Найти:
Стр.72, №230
∆АВС,
ВР,АТ - биссектрисы
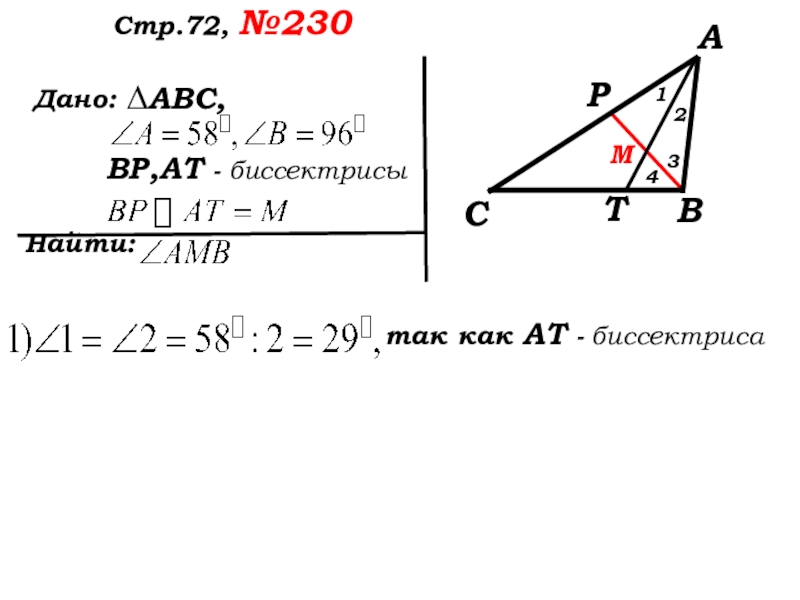
Анализируем условие
задачи.
Какой вывод можно сделать из 2 и 3 строки условия дано?
Какой вывод можно сделать из 2 и 3 строки условия дано?
3
1
2
4
Слайд 44 Дано:
Найти:
Стр.72, №230
∆АВС,
ВР,АТ - биссектрисы
3
1
2
4
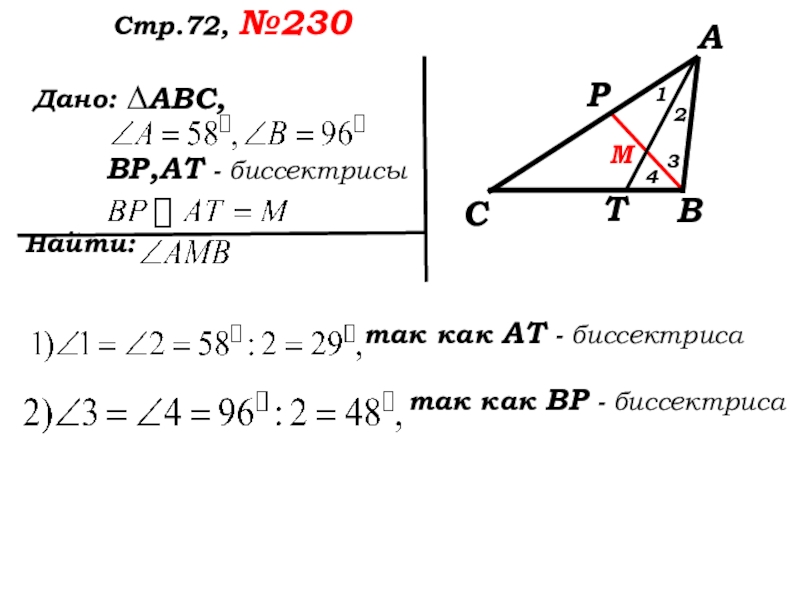
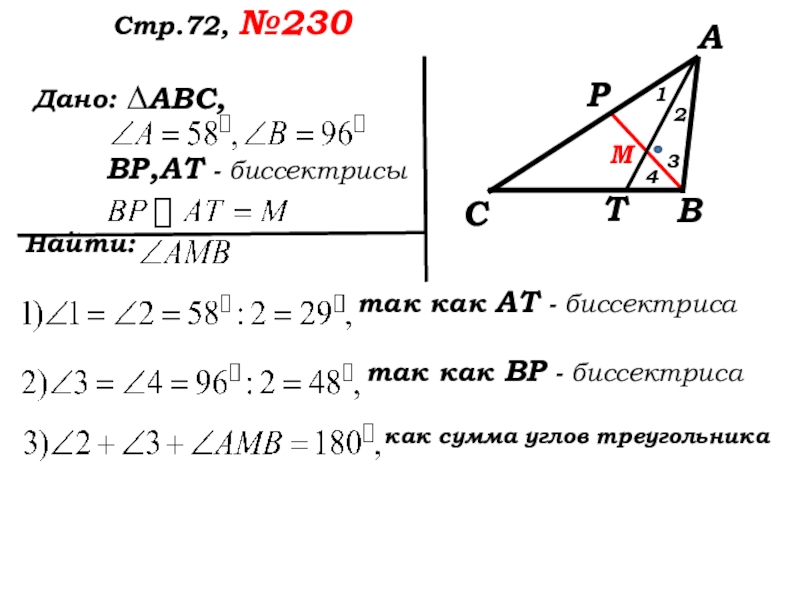
так как
АТ - биссектриса
так как ВР - биссектриса
Слайд 45 Дано:
Найти:
Стр.72, №230
∆АВС,
ВР,АТ - биссектрисы
3
1
2
4
так как
АТ - биссектриса
так как ВР - биссектриса
как сумма углов треугольника
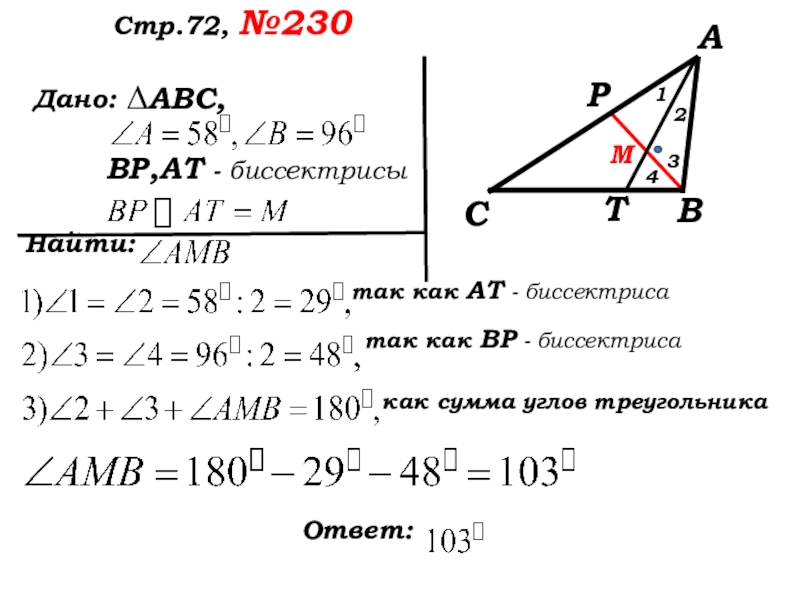
Слайд 46 Дано:
Найти:
Стр.72, №230
∆АВС,
ВР,АТ - биссектрисы
3
1
2
4
так как
АТ - биссектриса
так как ВР - биссектриса
как сумма углов треугольника
Слайд 47 Дано:
Найти:
Стр.72, №230
∆АВС,
ВР,АТ - биссектрисы
3
1
2
4
так как
АТ - биссектриса
так как ВР - биссектриса
как сумма углов треугольника
Ответ:
Слайд 48Стр.72, №231
Прочитайте задачу?
Что известно в треугольнике?
Что нужно доказать?
Какой треугольник дан в
задаче?
Какой следует выполнить чертёж?
Слайд 49 Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
Какой треугольник АВС чертим?
Слайд 50 Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
Обозначим треугольник и проведем медиану АМ
Слайд 51 Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
Какое условие задачи не отмечено на чертеже?
А
С
В
М
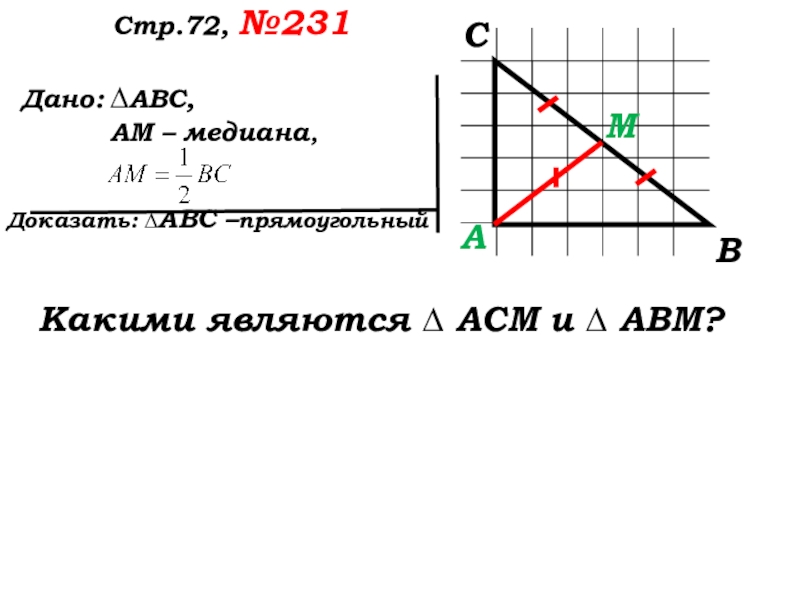
Слайд 52 Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
Какими являются ∆ АСМ и ∆ АВМ?
А
С
В
М
Слайд 53 Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
А
С
В
М
1
2
3
4
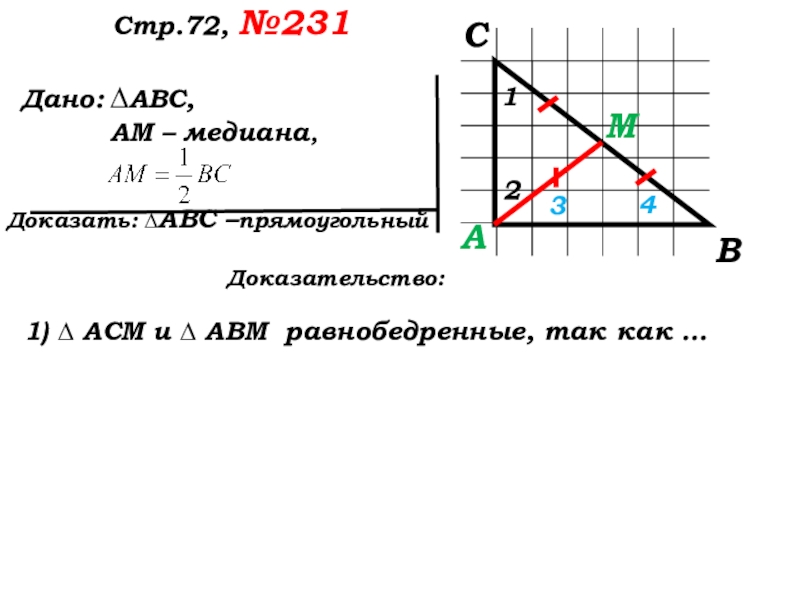
Доказательство:
1) ∆ АСМ и ∆ АВМ равнобедренные, так как …
Слайд 54 Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
А
С
В
М
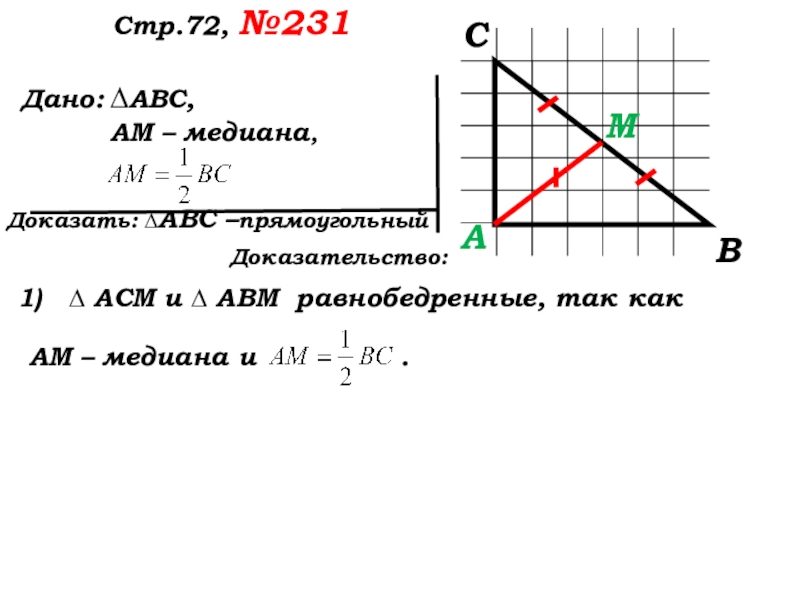
Доказательство:
∆ АСМ и ∆ АВМ равнобедренные, так как
АМ – медиана и .
Слайд 55 Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
А
С
В
М
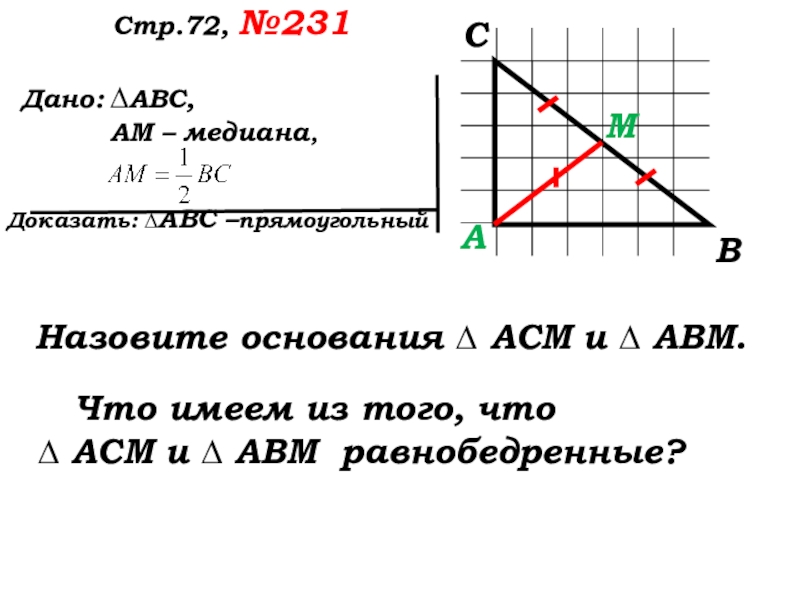
Назовите основания ∆ АСМ и ∆ АВМ.
Что имеем из того, что
∆ АСМ и ∆ АВМ равнобедренные?
Слайд 56 Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
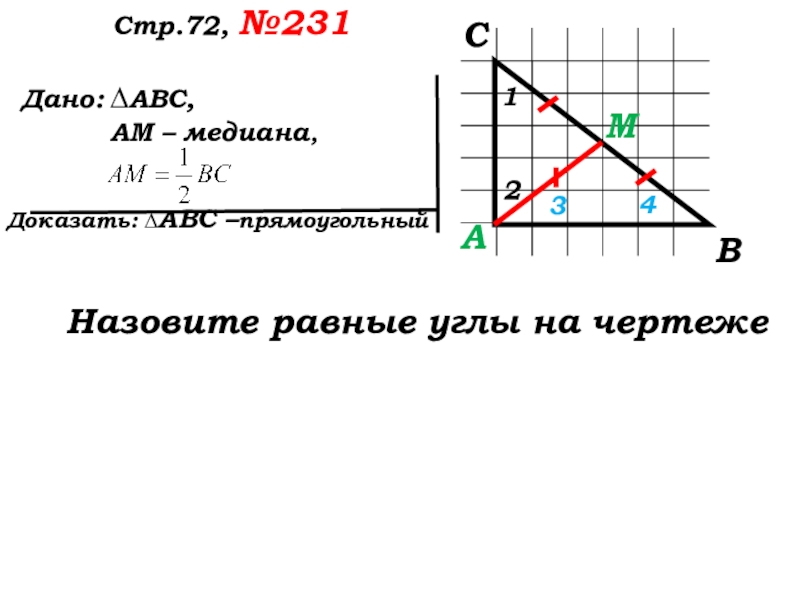
Назовите равные углы на чертеже
А
С
В
М
1
2
3
4
Слайд 57 Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
А
С
В
М
1
2
3
4
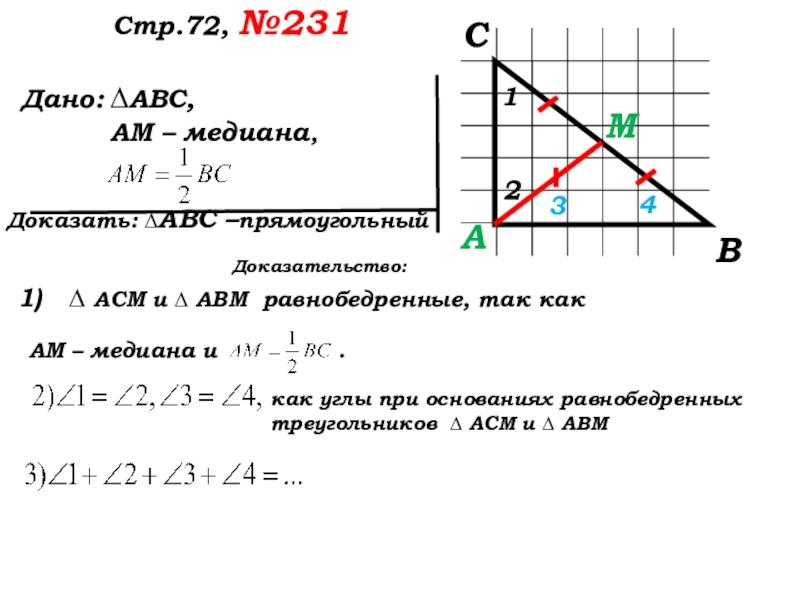
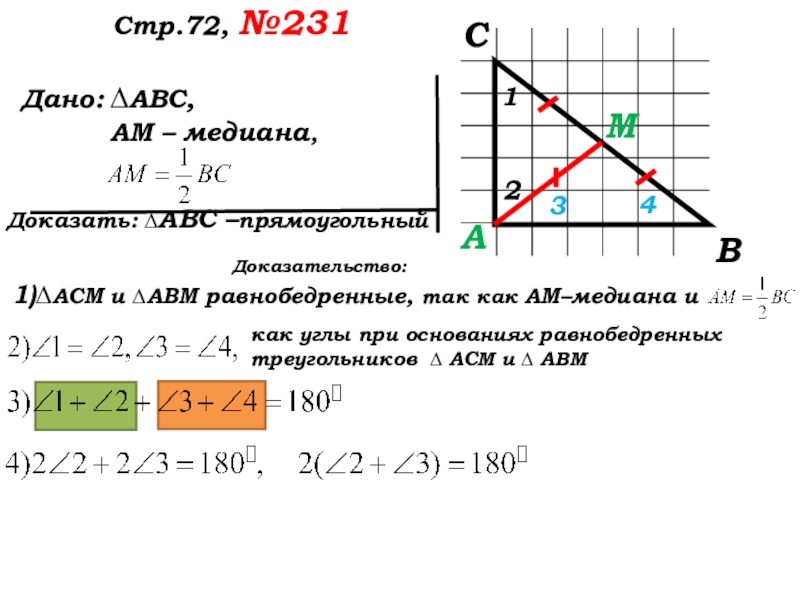
Доказательство:
∆ АСМ и ∆ АВМ равнобедренные, так как
АМ – медиана и .
как углы при основаниях равнобедренных треугольников
∆ АСМ и ∆ АВМ
Слайд 58 Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
А
С
В
М
1
2
3
4
Доказательство:
∆ АСМ и ∆ АВМ равнобедренные, так как
АМ – медиана и .
как углы при основаниях равнобедренных треугольников ∆ АСМ и ∆ АВМ
Слайд 59 Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
А
С
В
М
1
2
3
4
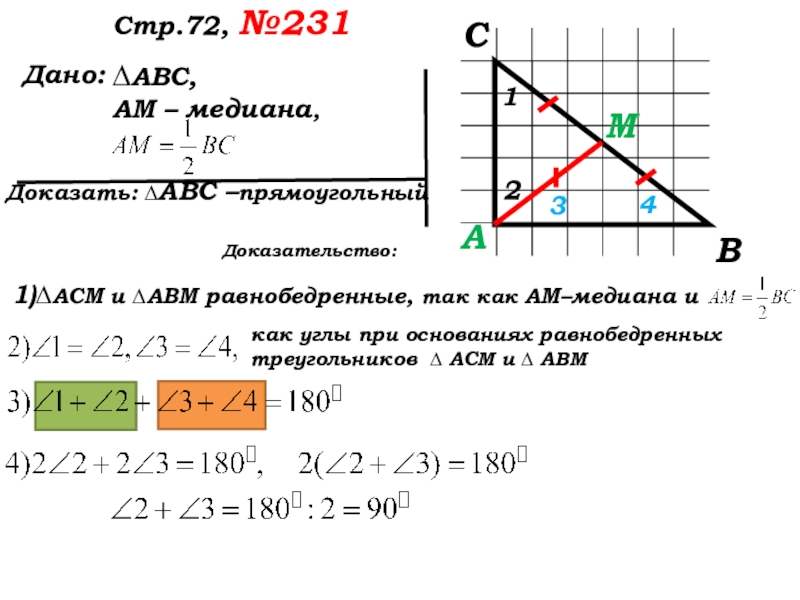
Доказательство:
∆ АСМ и ∆ АВМ равнобедренные, так как
АМ – медиана и .
как углы при основаниях равнобедренных треугольников ∆ АСМ и ∆ АВМ
Слайд 60
Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
А
С
В
М
1
2
3
4
Доказательство:
∆ АСМ и ∆ АВМ равнобедренные, так как
АМ – медиана и .
как углы при основаниях равнобедренных треугольников ∆ АСМ и ∆ АВМ
Слайд 61
Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
А
С
В
М
1
2
3
4
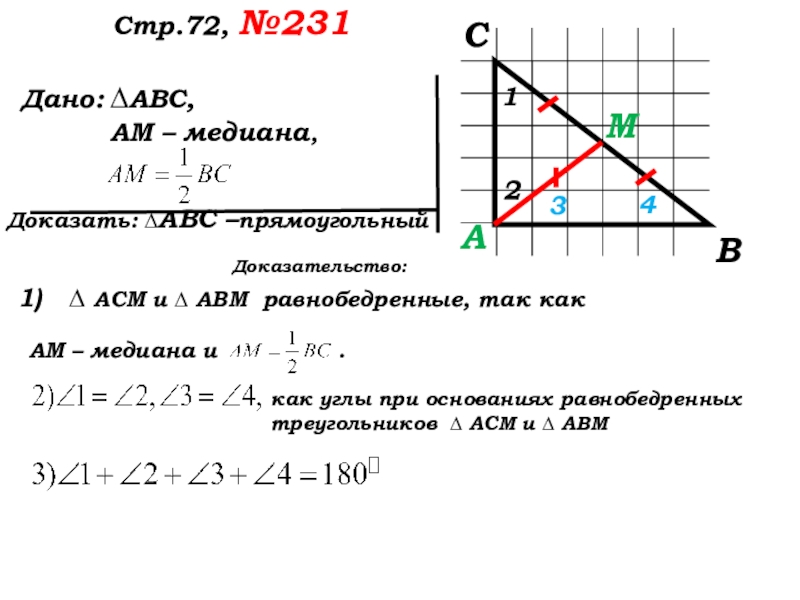
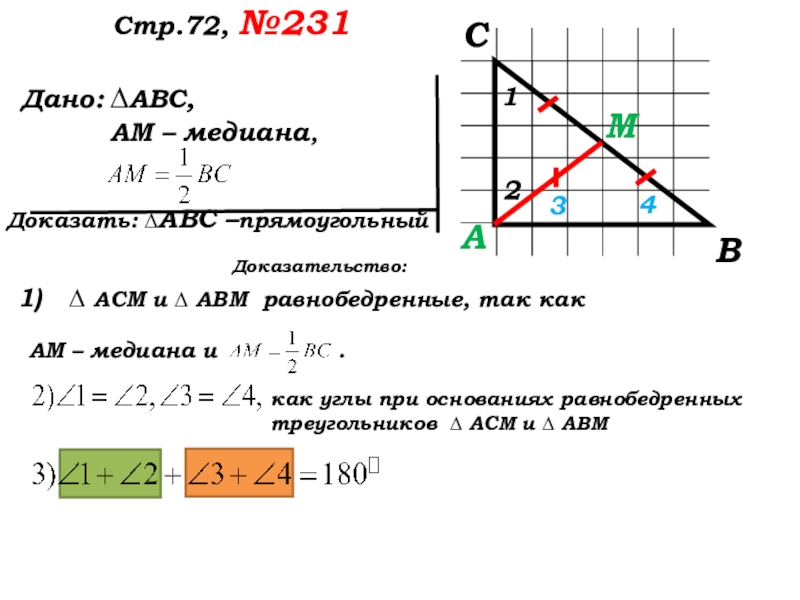
Доказательство:
1)∆АСМ и ∆АВМ равнобедренные, так как АМ–медиана и
как углы при основаниях равнобедренных треугольников ∆ АСМ и ∆ АВМ
Слайд 62
Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
А
С
В
М
1
2
3
4
Доказательство:
1)∆АСМ и ∆АВМ равнобедренные, так как АМ–медиана и
как углы при основаниях равнобедренных треугольников ∆ АСМ и ∆ АВМ
Слайд 63
Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
А
С
В
М
1
2
3
4
Доказательство:
1)∆АСМ и ∆АВМ равнобедренные, так как АМ–медиана и
как углы при основаниях равнобедренных треугольников ∆ АСМ и ∆ АВМ
Слайд 64
Дано:
Доказать: ∆АВС –прямоугольный
Стр.72, №231
∆АВС,
АМ
– медиана,
А
С
В
М
1
2
3
4
Доказательство:
1)∆АСМ и ∆АВМ равнобедренные, так как АМ–медиана и
как углы при основаниях равнобедренных треугольников ∆ АСМ и ∆ АВМ
Слайд 65
Дано:
Доказать:
Стр.72, №231
∆АВС,
АМ – медиана,
А
С
В
М
1
2
3
4
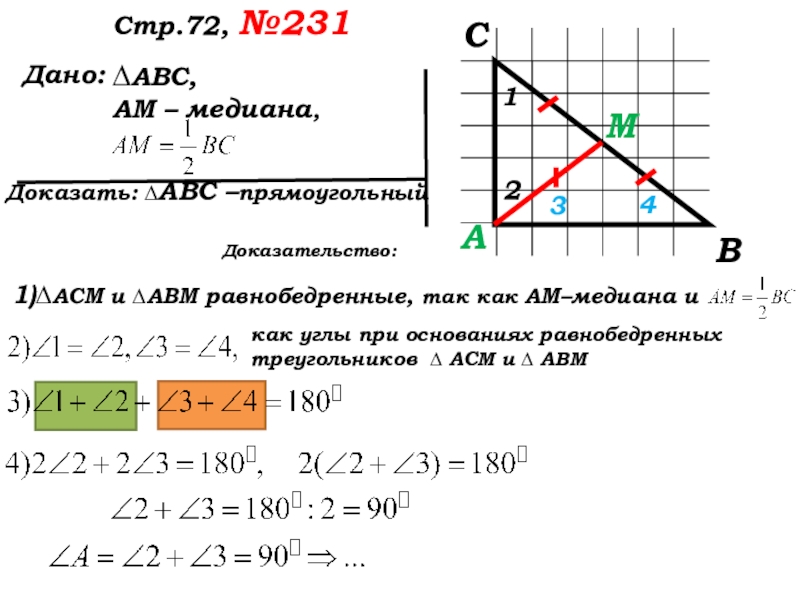
Доказательство:
1)∆АСМ
и ∆АВМ равнобедренные, так как АМ–медиана и
как углы при основаниях равнобедренных треугольников ∆ АСМ и ∆ АВМ
∆АВС –прямоугольный. Чтд.
∆АВС –прямоугольный
Слайд 67Вывод:
Биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию этого треугольника
Стр.72,
№233
1
2
3
Слайд 70Д.Р № 39
Глава 4,§1, пп.30-31
Знать: теорему, опр. внешнего угла, опр.
видов треугольника
Записи в тетради
Стр.71, №229,234, 235*
В обязательном порядке иметь все геометрические инструменты:
линейка, треугольник, транспортир, циркуль, карандаш
Записи в тетради
Стр.71, №229,234, 235*
В обязательном порядке иметь все геометрические инструменты:
линейка, треугольник, транспортир, циркуль, карандаш
