- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Цилиндр (11 класс)
Содержание
- 1. Презентация по геометрии на тему Цилиндр (11 класс)
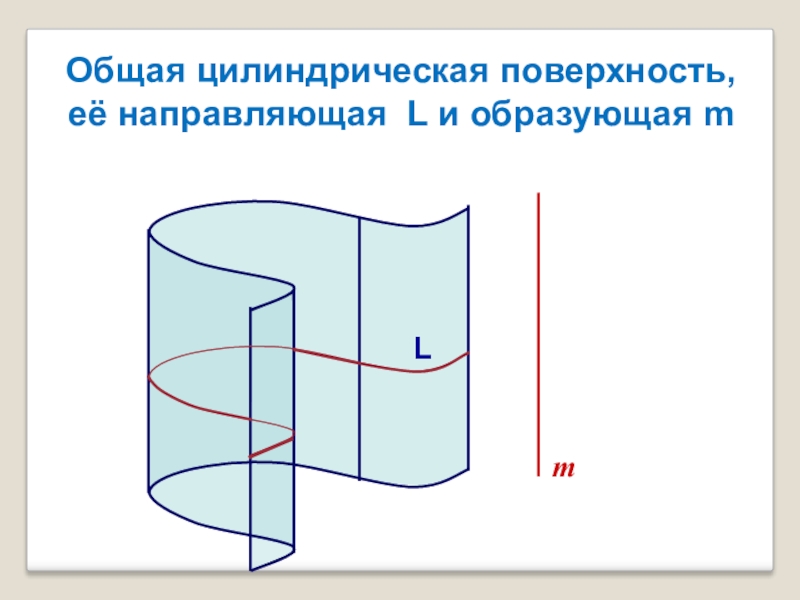
- 2. LmОбщая цилиндрическая поверхность, её направляющая L и образующая m
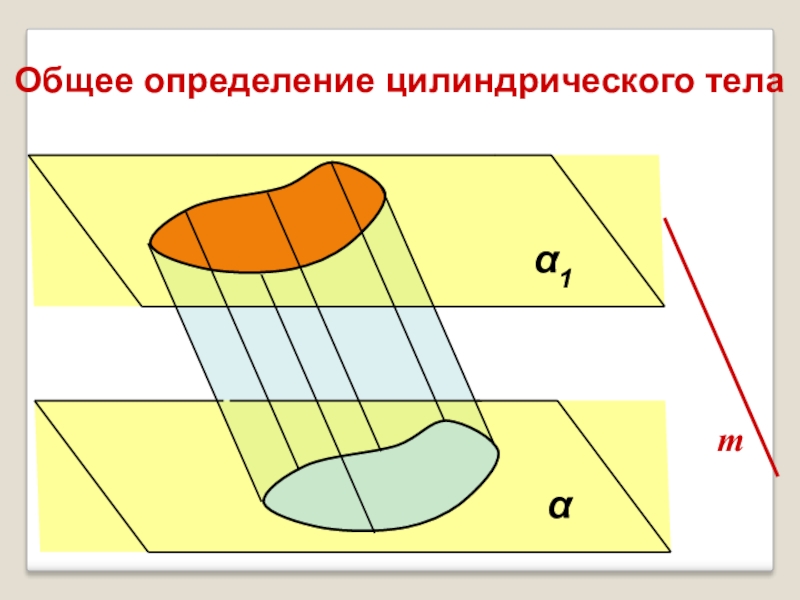
- 3. Общее определение цилиндрического телаmαα1
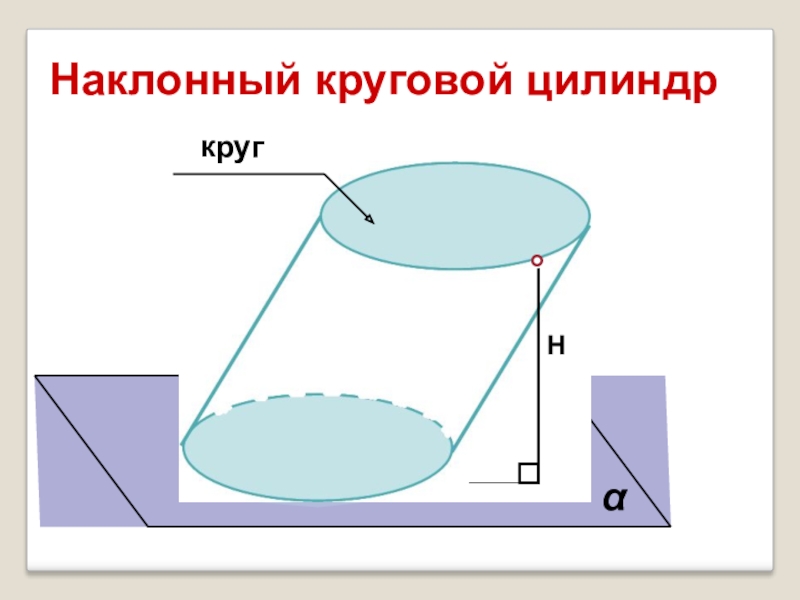
- 4. Наклонный круговой цилиндрНкругα
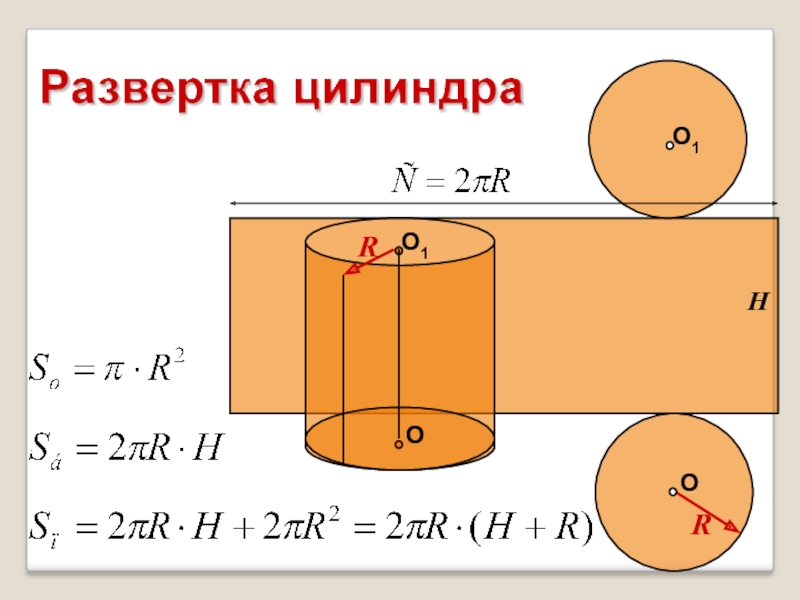
- 5. ОО1Прямой круговой цилиндроснованиеобразующаяось цилиндрабоковая поверхность
- 6. RRH
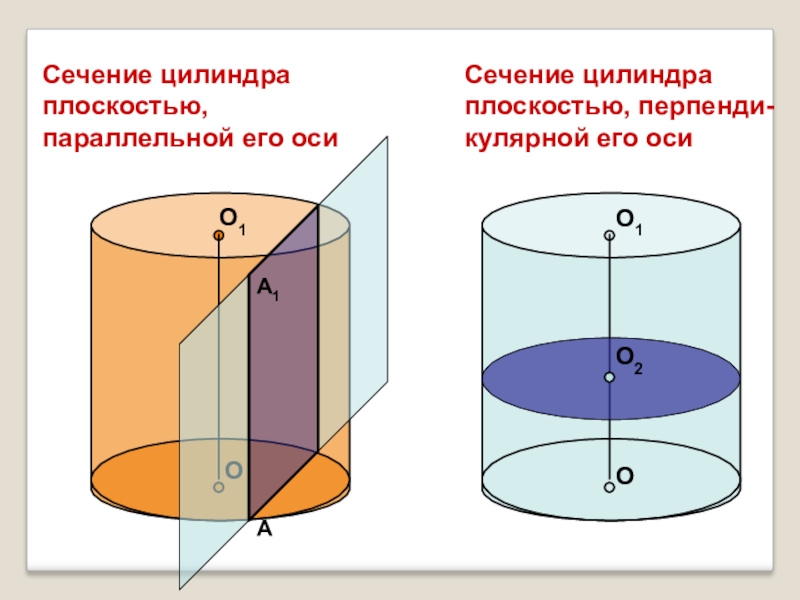
- 7. Сечение цилиндра плоскостью, параллельной его осиОО1Сечение цилиндра плоскостью, перпенди-кулярной его осиАА1
- 8. Найдите площадь поверхности (внешней и внутренней) шляпы,
- 9. №523Осевое сечение цилиндра – квадрат, диагональ которого
- 10. №525Площадь осевого сечения цилиндра равна 10 м2,
- 11. №527Концы отрезка АВ лежат на разных основаниях
- 12. rardКСПостроим отрезок d (расстояние между скрещивающимися прямыми
- 13. AА1C1В1№532Через образующую АА1 цилиндра проведены две секущие
- 14. Плоскость γ, параллельная оси цилиндра, отсекает от
- 15. Повторить стр.130-132, гл. 1, п.59-60, №530, №
Слайд 7
Сечение цилиндра плоскостью, параллельной его оси
О
О1
Сечение цилиндра плоскостью, перпенди-кулярной его оси
А
А1
Слайд 8Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см)
1) Если дно шляпы опустить на плоскость её полей, то получим круг радиуса
R = r1+ 10 = 20 cм.
2) Площадь этого круга
3) Найдем площадь боковой поверхности цилиндрической части
4) Найдем площадь шляпы
Ответ: 1600π (см2).
r1=10
10
10
Решение.
Слайд 9
№523
Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите:
Решение.
1. Проведем диагональ АС сечения АВСD.
A
B
C
D
2. ΔADC – равнобедренный, прямоугольный, АD=DC, h = 2r,
⇒ ∠CAD = ∠ACD=45°, тогда
20
3. Найдем радиус основания
4. Найдем площадь основания
Ответ:
Слайд 10
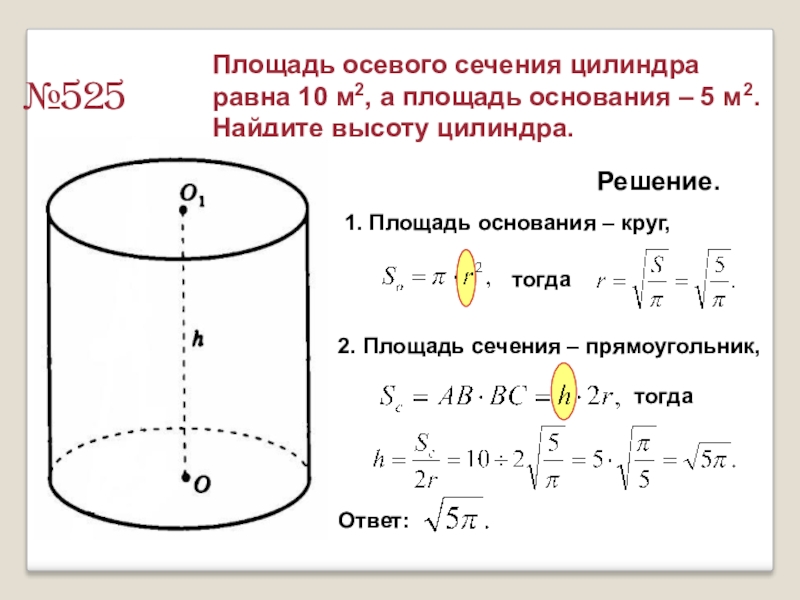
№525
Площадь осевого сечения цилиндра равна 10 м2, а площадь основания –
Решение.
1. Площадь основания – круг,
тогда
2. Площадь сечения – прямоугольник,
тогда
Ответ:
Слайд 11
№527
Концы отрезка АВ лежат на разных основаниях цилиндра. Радиус цилиндра равен
r
a
Решение.
1. Построим отрезок АВ.
2. Проведем радиус АО.
3. Построим отрезок d.
?
r
d
К
4. Отрезок ОК – искомое расстояние.
5. Из прямоугольного ΔАОК находим:
С
значит АС = 12.
6. Из прямоугольного ΔАВС находим:
Итак, h = 5.
Ответ: 5.
Слайд 12
r
a
r
d
К
С
Построим отрезок d
(расстояние между скрещивающимися прямыми АВ и ОО1).
1) Построим
2) Построим радиусы АО и СО.
3) ΔАОС – равнобедренный, проведем высоту ОК, она и будет искомым расстоянием, т.к. прямая ОК перпендикулярна к двум пересекающимся прямым АС и ВС плоскости АВС.
Слайд 13A
А1
C1
В1
№532
Через образующую АА1 цилиндра проведены две секущие плоскости, одна из которых
В
C
Решение.
1) Сделаем чертеж, построим плоскости АА1В1В и АА1С1С.
3) Построим плоскость ВВ1С1С.
4) Заметим, что АВ диаметр основания цилиндра, значит ∠АСВ=90°, тогда
2) Составим отношение площадей сечений
5) Итак,
Слайд 14Плоскость γ, параллельная оси цилиндра, отсекает от окружности основания дугу AmD
1) Докажите, что сечение цилиндра плоскостью γ есть прямоугольник.
2) Найдите AD, если a = 8 см, α = 120°.
1) Составьте план вычисления площади сечения по данным α, h, d.
2) Найдите AD, если a = 10 см, α = 60°.
Самостоятельная работа
Ответ:
10
Ответ:
Слайд 15Повторить стр.130-132, гл. 1, п.59-60,
№530, № 537.
Что нового вы узнали
Домашнее задание
Рефлексия
Можете ли вы объяснить решение данных задач однокласснику, пропустившему урок сегодня?
Чему вы научились?
Какое у вас настроение в конце урока?
Спасибо, за урок!