- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Пифагора
Содержание
- 1. Презентация по геометрии на тему Теорема Пифагора
- 2. «Да, путь познания не гладок.Но знаем мы со школьных лет,Загадок больше, чем разгадок,И поискам предела нет!»
- 3. Старинная задачаНа
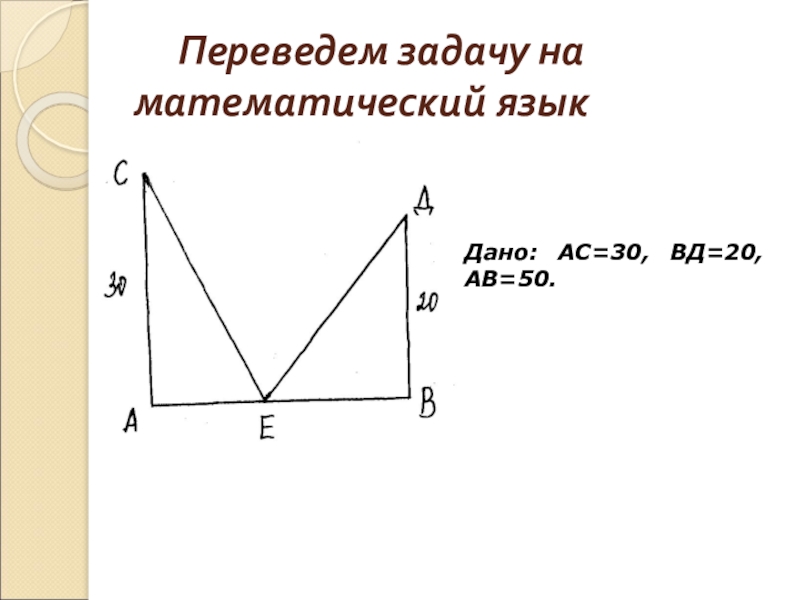
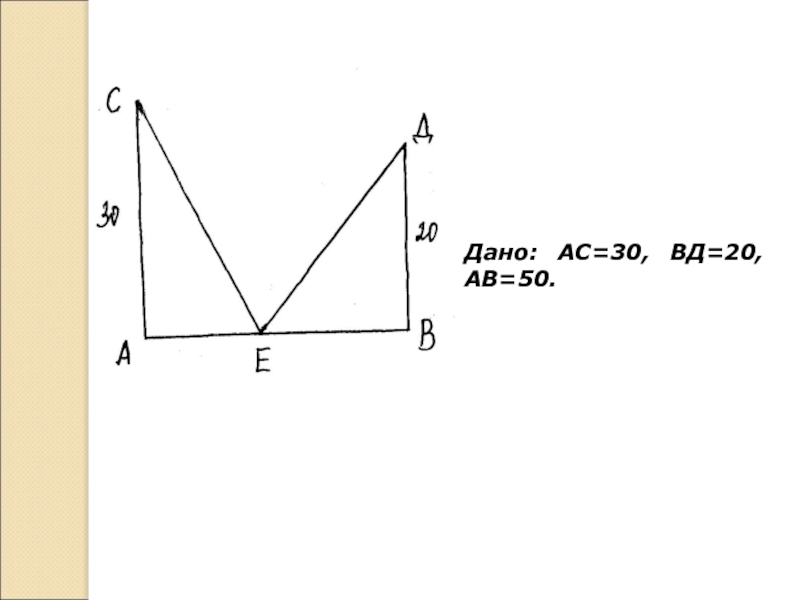
- 4. Переведем задачу на математический языкДано: АС=30, ВД=20, АВ=50.
- 5. Нужно знать зависимость между катетами и гипотенузой
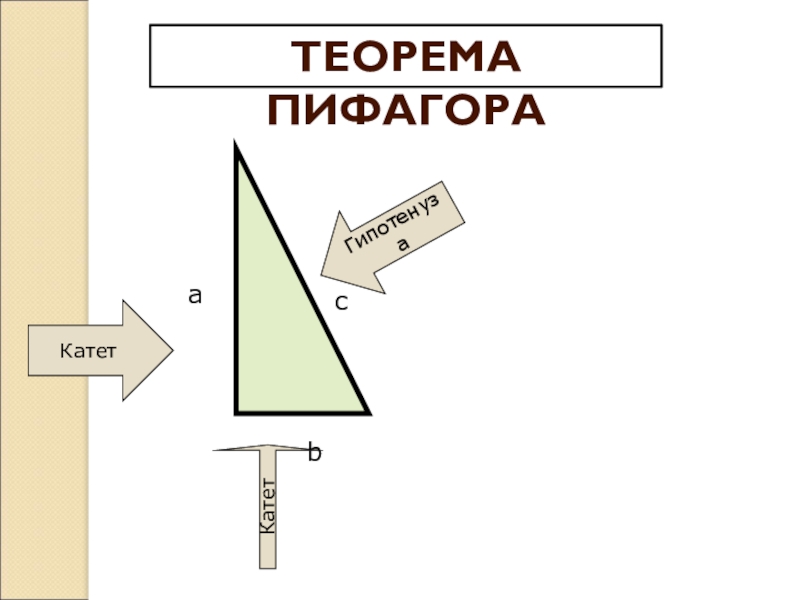
- 6. ТЕОРЕМА ПИФАГОРА
- 7. «Геометрия владеет многими сокровищами: одно из них – это теорема Пифагора»
- 8. Теорема Пифагора - одна из важнейших теорем
- 9. Биография Пифагора Пифагор-это не имя,
- 10. Пифагорейская школа Вернувшись на родину,
- 11. Пифагорейская школа Пифагорейцы занимались
- 12. Заповеди Пифагора и
- 13. Заповеди пифагорийцевДелать то, что
- 14. Это прямоугольный треугольникТЕОРЕМА ПИФАГОРА
- 15. аcbКатетКатетГипотенузаТЕОРЕМА ПИФАГОРА
- 16. «Площадь квадрата, построенного на гипотенузе прямо-угольного треугольника,
- 17. Если дан нам треугольникИ притом с прямым
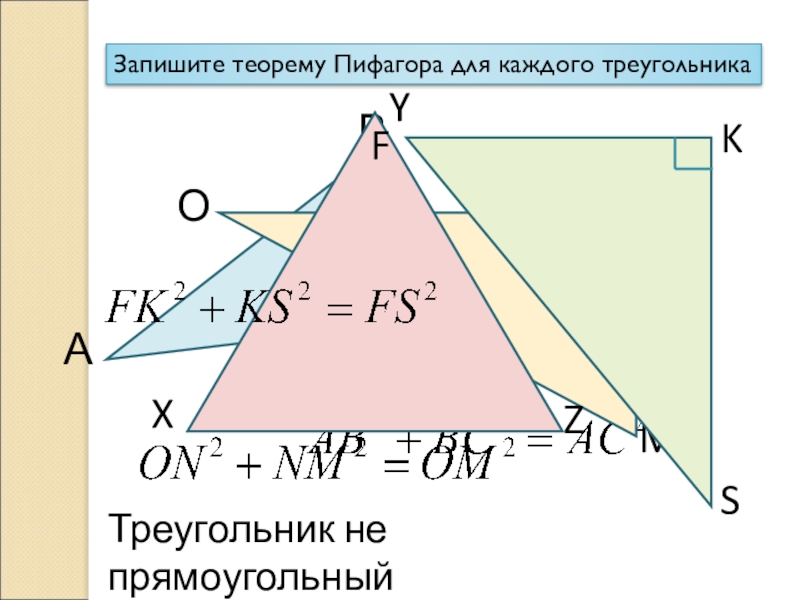
- 18. Запишите теорему Пифагора для каждого треугольникаАВСОNMXYZТреугольник не прямоугольныйFKS
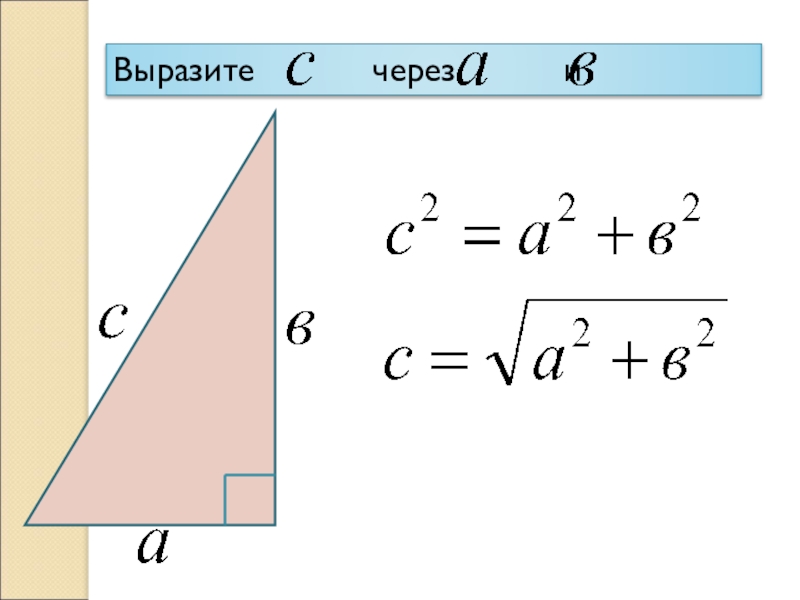
- 19. Выразите через и
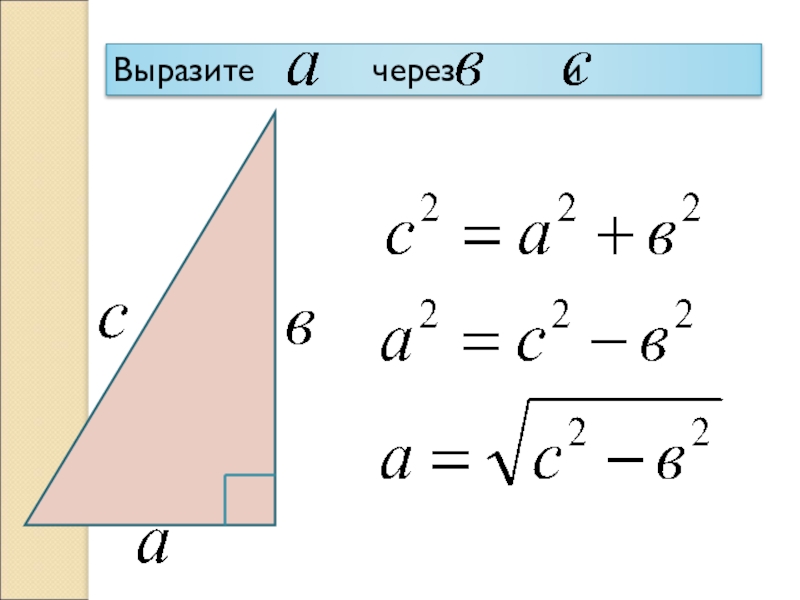
- 20. Выразите через и
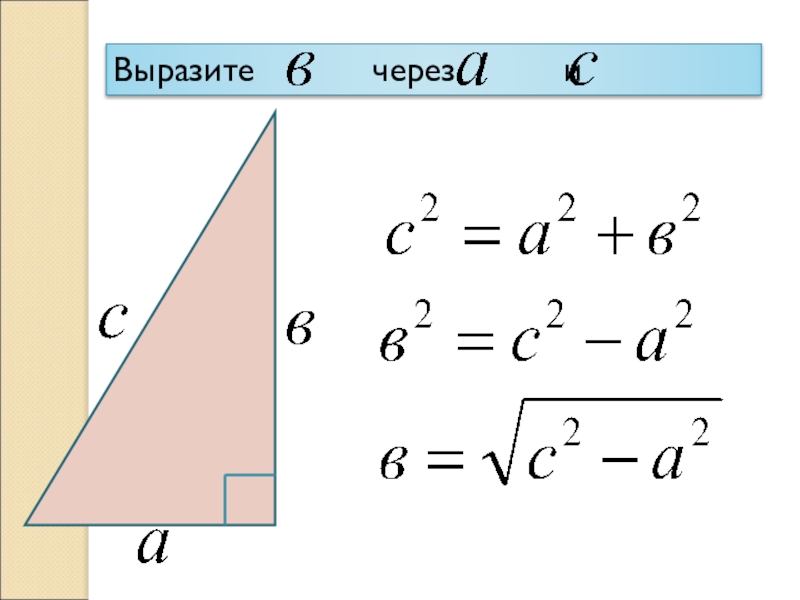
- 21. Выразите через и
- 22. Дано:АВС прямоугольный треугольник,Найти:ВАСОтвет:
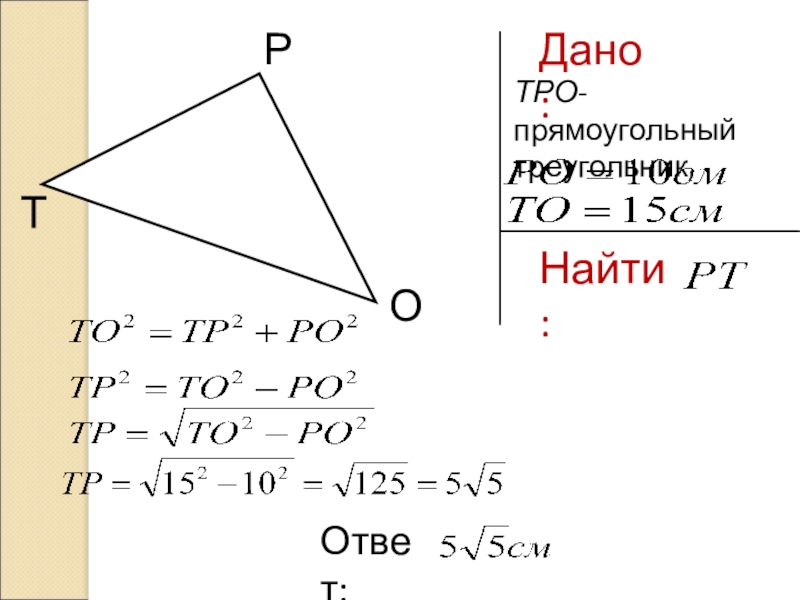
- 23. Дано:ТРО-прямоугольный треугольник,Найти:РТООтвет:
- 24. А сейчас вернемся к нашей задачеНа обоих
- 25. Дано: АС=30, ВД=20, АВ=50.
- 26. Вам, наверное, известны также детские стишки о
- 27. До нас дошли и другие шуточные рисунки к теореме
- 28. Рассмотрим еще одну задачу, для решения которой
- 29. Слайд 29
- 30. Сформулируйте теорему ПифагораСформулируйте теорему, обратную теореме ПифагораЕсли
- 31. Древние египтяне для построения прямоугольных треугольников
- 32. Треугольник со сторонами 3, 4, 5 теперь мы называем египетским.
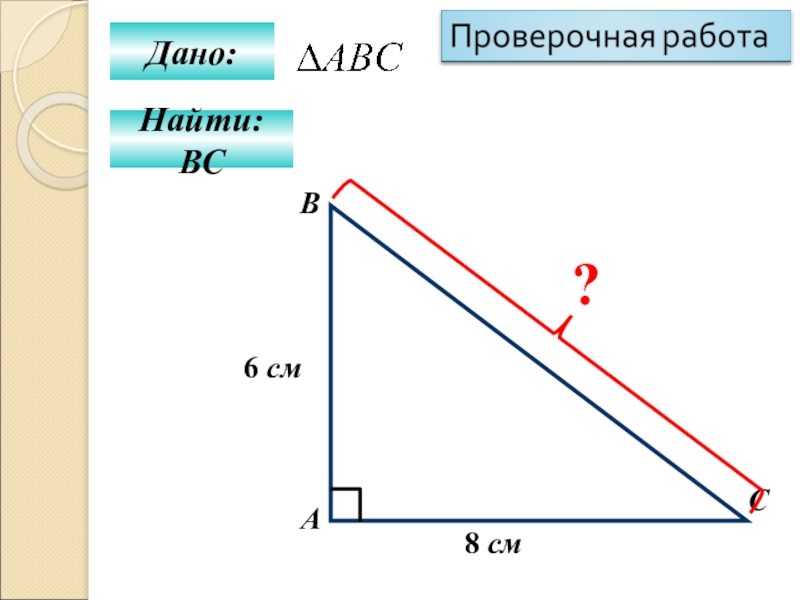
- 33. Найти: ВССВАДано:8 см6 см?
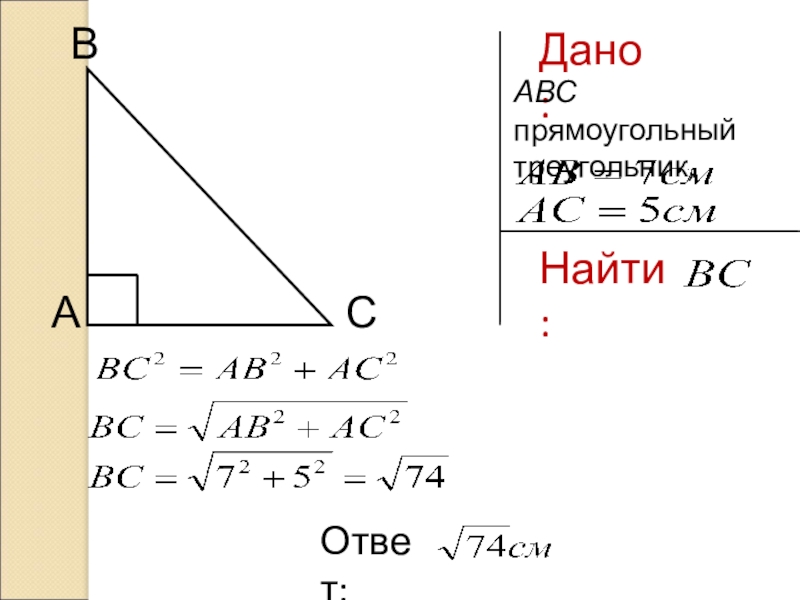
- 34. Дано:СВНайти: ВСА5 см7 см?
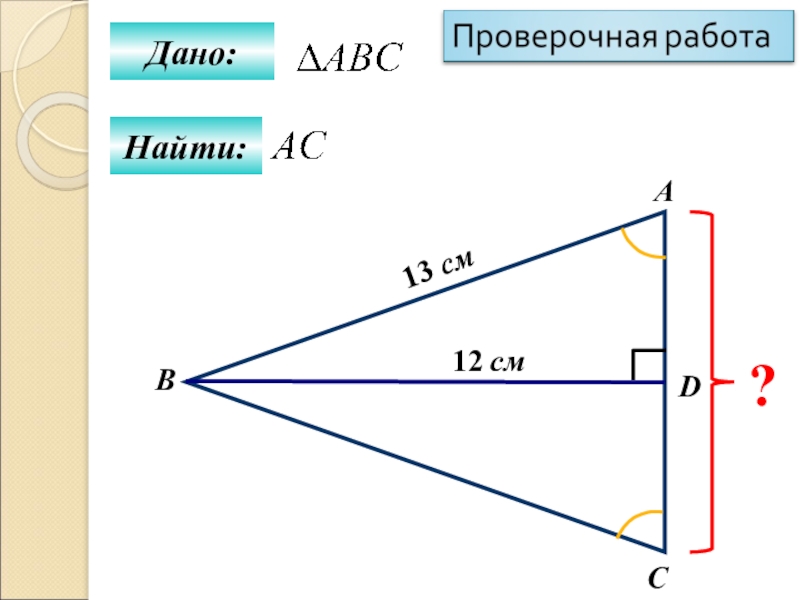
- 35. Дано:Найти:АBCD?12 см13 см
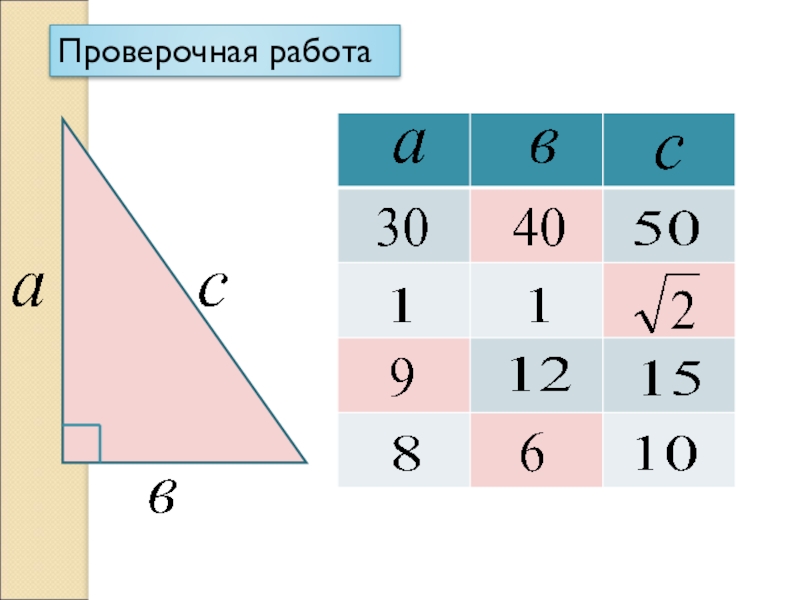
- 36. Проверочная работа
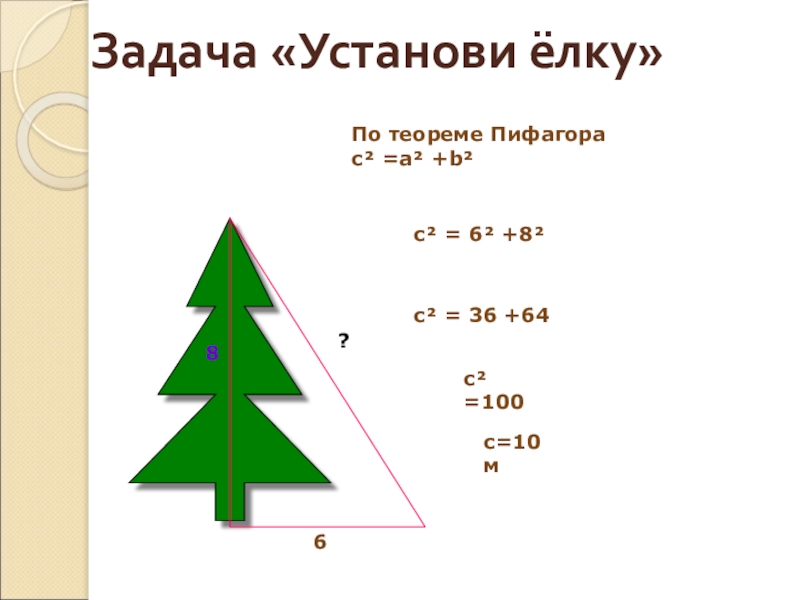
- 37. Задача «Установи ёлку»86?По теореме Пифагорас² =а² +b²с² = 6² +8²с² = 36 +64с² =100с=10м
- 38. Задача индийского математика XII века БхаскарыИСТОРИЧЕСКИЕ ЗАДАЧИ
- 39. Задача из китайской "Математики в девяти
- 40. Задача из учебника "Арифметика" Леонтия Магницкого«Случися
«Да, путь познания не гладок.Но знаем мы со школьных лет,Загадок больше, чем разгадок,И поискам предела нет!»
Слайд 2«Да, путь познания не гладок.
Но знаем мы со школьных лет,
Загадок больше,
чем разгадок,
И поискам предела нет!»
И поискам предела нет!»
Слайд 3 Старинная задача
На обоих берегах реки растет
по пальме, одна против другой. Высота одной 30 локтей, другой 20 локтей. Расстояние между их основаниями 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременною. На каком расстоянии от более высокой пальмы появилась рыба.
Слайд 5Нужно знать зависимость между катетами и гипотенузой в прямоугольном треугольнике.
Эту зависимость
подметили еще в глубокой древности и доказали теорему, которую знают теперь почти все.
Эта теорема носит имя Пифагора.
Эта теорема носит имя Пифагора.
Слайд 8Теорема Пифагора - одна из важнейших теорем геометрии.
Она является основой
решения
множества
геометрических задач
и базой изучения
теоретического
материала в
дальнейшем.
геометрических задач
и базой изучения
теоретического
материала в
дальнейшем.
Слайд 9Биография Пифагора
Пифагор-это не имя, а прозвище, данное ему
за то , что он высказывал истину также постоянно, как дельфийский аракул.
«Пифагор» значит «убеждающий речью» жил в Древней Греции.
О жизни его известно немного, зато с именем его связан ряд легенд. Рассказывают, что он много путешествовал, изучал древнюю культуру и достижения науки разных стран.
«Пифагор» значит «убеждающий речью» жил в Древней Греции.
О жизни его известно немного, зато с именем его связан ряд легенд. Рассказывают, что он много путешествовал, изучал древнюю культуру и достижения науки разных стран.
Слайд 10Пифагорейская школа
Вернувшись на родину, Пифагор
организовал кружок молодежи из
представителей аристократии. В
кружок принимались с большими
церемониями после долгих испытаний.
Каждый вступающий отрекался от
своего имущества и давал клятву
хранить в тайне учения основателя.
Так на юге Италии, которая была
тогда греческой колонией, возникла
пифагорейская школа.
представителей аристократии. В
кружок принимались с большими
церемониями после долгих испытаний.
Каждый вступающий отрекался от
своего имущества и давал клятву
хранить в тайне учения основателя.
Так на юге Италии, которая была
тогда греческой колонией, возникла
пифагорейская школа.
Слайд 11Пифагорейская школа
Пифагорейцы занимались
математикой, философией,
естественными науками.
Ими было сделано много важных открытий в арифметике и геометрии.
В школе существовал декрет, по которому авторство всех математических работ
приписывалось Пифагору.
Звездчатый пятиугольник, или пентаграмма, - пифагорейский символ здравия и тайный опознавательный знак
Слайд 12 Заповеди Пифагора
и его учеников актуальны
и сейчас и могут быть
приемлемы для любого здравомыслящего человека.
Вот они!
приемлемы для любого здравомыслящего человека.
Вот они!
Слайд 13 Заповеди пифагорийцев
Делать то, что впоследствии не огорчит тебя
и не принудит раскаиваться;
Не делай никогда того, что не знаешь, но научись всему, что следует знать;
Не пренебрегай здоровьем своего тела;
Приучайся жить просто и без роскоши.
Не делай никогда того, что не знаешь, но научись всему, что следует знать;
Не пренебрегай здоровьем своего тела;
Приучайся жить просто и без роскоши.
Слайд 16
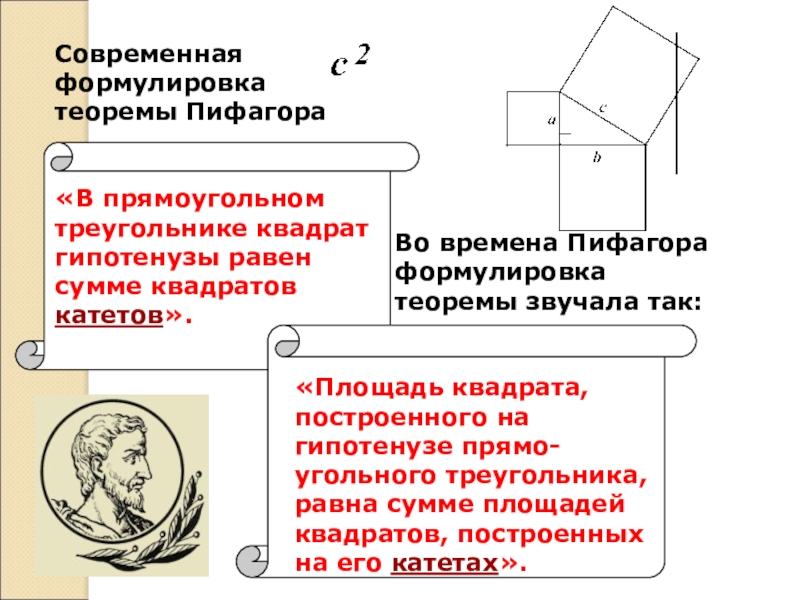
«Площадь квадрата, построенного на гипотенузе прямо-угольного треугольника, равна сумме площадей квадратов,
построенных на его катетах».
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов катетов».
Во времена Пифагора формулировка теоремы звучала так:
Современная формулировка
теоремы Пифагора
Слайд 17Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда
легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придем.
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придем.
И. Дырченко
Слайд 24А сейчас вернемся к нашей задаче
На обоих берегах реки растет по
пальме, одна против другой. Высота одной 30 локтей, другой 20 локтей. Расстояние между их основаниями 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременною. На каком расстоянии от более высокой пальмы появилась раба.
Слайд 26Вам, наверное, известны также детские стишки о пифагоровых штанах. Данный рисунок
подтверждает их содержание.
Пифагоровы штаны
Во все стороны равны.
Слайд 28Рассмотрим еще одну задачу, для решения которой нам необходимо знать теорему
Пифагора.
Над озером тихим,
С полфута размером,
Высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону.
Нет боле цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода глубока?
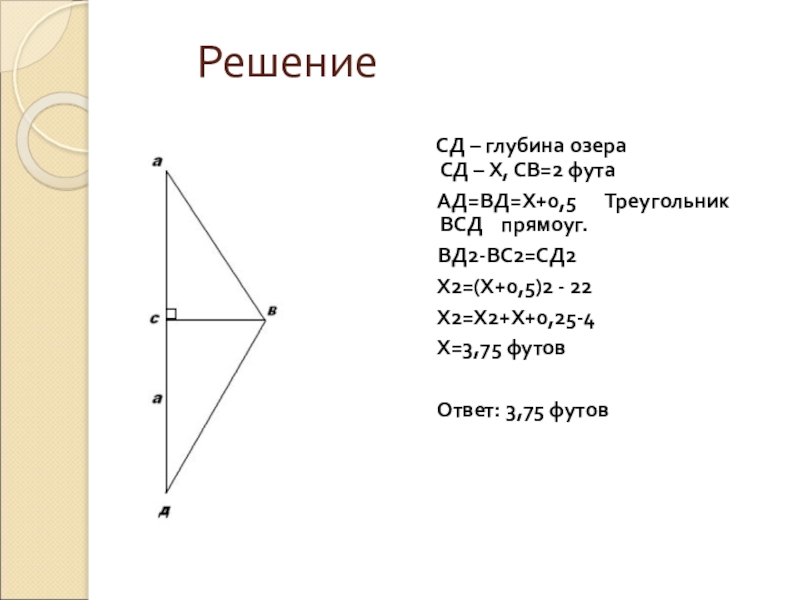
Слайд 29 Решение
СД – глубина озера СД – Х, СВ=2 фута
АД=ВД=Х+0,5 Треугольник ВСД прямоуг.
ВД2-ВС2=СД2
Х2=(Х+0,5)2 - 22
Х2=Х2+Х+0,25-4
Х=3,75 футов
Ответ: 3,75 футов
АД=ВД=Х+0,5 Треугольник ВСД прямоуг.
ВД2-ВС2=СД2
Х2=(Х+0,5)2 - 22
Х2=Х2+Х+0,25-4
Х=3,75 футов
Ответ: 3,75 футов
Слайд 30Сформулируйте теорему Пифагора
Сформулируйте теорему, обратную теореме Пифагора
Если в треугольнике квадрат большей
стороны равен сумме квадратов двух других сторон, то этот треугольник будет прямоугольным.
Слайд 31 Древние египтяне для построения прямоугольных треугольников пользовались веревкой с завязанными
на ней на одинаковых расстояниях узелками. По одной стороне они откладывали 3 отрезка, на другой 4, а на третьей 5.
Правильно ли они поступали?
Правильно ли они поступали?
Слайд 39Задача из китайской
"Математики в девяти книгах"
"Имеется водоем со стороной в
1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его.
Спрашивается: какова глубина воды и какова длина камыша?"
Спрашивается: какова глубина воды и какова длина камыша?"
ИСТОРИЧЕСКИЕ ЗАДАЧИ
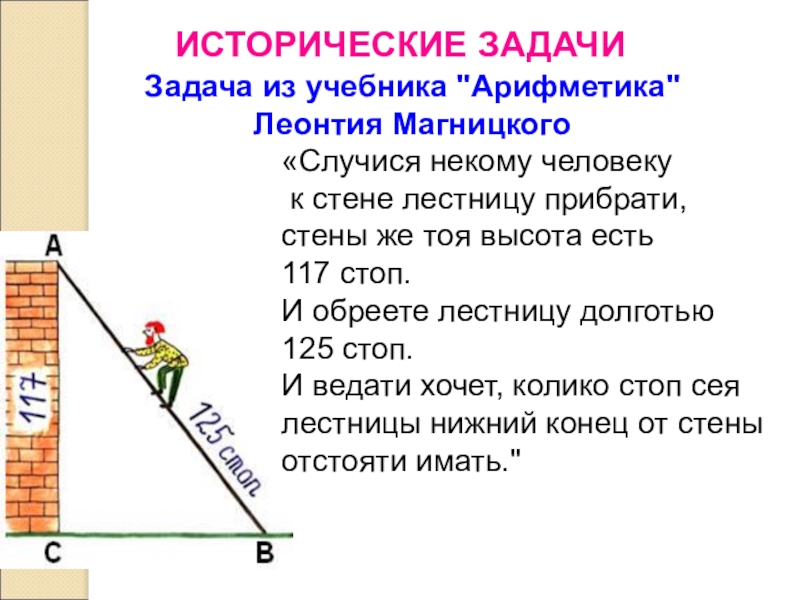
Слайд 40Задача из учебника "Арифметика"
Леонтия Магницкого
«Случися некому человеку
к стене лестницу
прибрати, стены же тоя высота есть
117 стоп.
И обреете лестницу долготью 125 стоп.
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."
117 стоп.
И обреете лестницу долготью 125 стоп.
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."
ИСТОРИЧЕСКИЕ ЗАДАЧИ
