- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Менелая и теорема Чевы(10 класс)
Содержание
- 1. Презентация по геометрии на тему Теорема Менелая и теорема Чевы(10 класс)
- 2. Теорема ЧевыПусть в ∆ABC на сторонах BC,AC,AB
- 3. Теорема МенелаяПусть на сторонах AB, BC и
- 4. Практическое применение теорем1. Теорема Менелая и пропорциональные
- 5. Теорема Менелая и пропорциональные отрезки в треугольникеЗадача
- 6. Теорема Чевы и ее следствия. Следствие1. Медианы
- 7. Теорема Чевы и ее следствия. Следствие4. Серединные
- 8. Применение теорем Чевы и Менелая к задачам
- 9. Задачи на пропорциональное деление отрезков в треугольнике.
- 10. Задачи на пропорциональное деление отрезков в треугольнике.
- 11. Задачи, связанные с нахождением
- 12. Комбинированные задачи. Задача 1. На стороне NP
- 13. «Теорема Менелая и теорема Чевы» в курсе
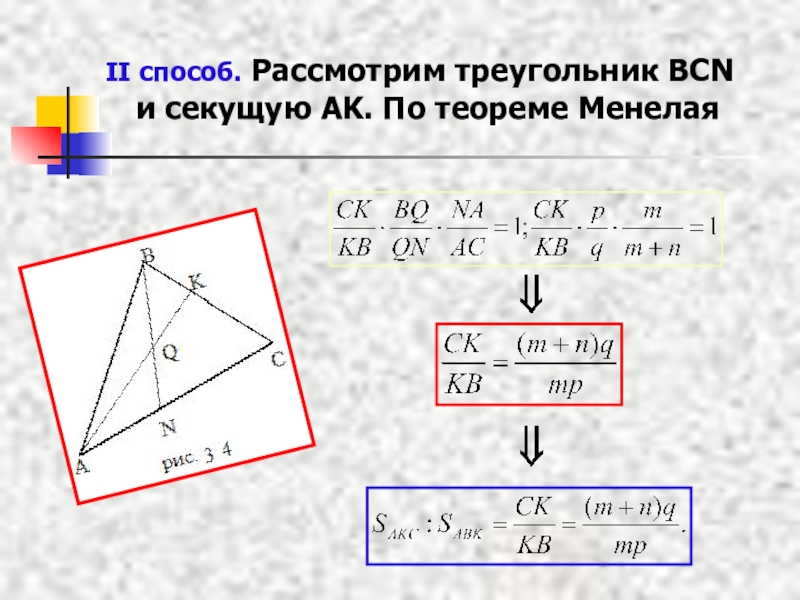
- 14. II способ. Рассмотрим треугольник BCN и секущую AK. По теореме Менелая
- 15. Задача. В равнобедренном треугольнике ABC (AС=BC) проведены
- 16. Применение теорем Менелая и Чевы в решении
- 17. Применение теорем Менелая и Чевы в решении
- 18. «Умение решать задачи- такое же
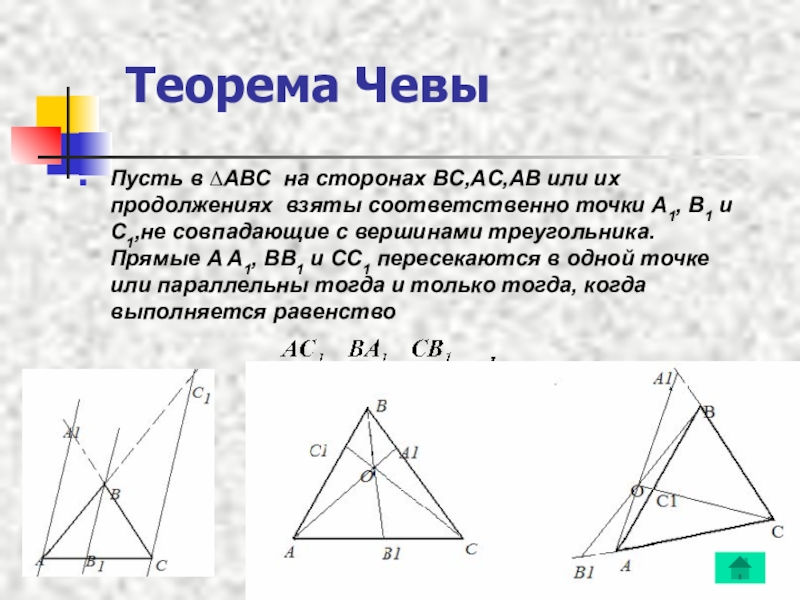
Слайд 2Теорема Чевы
Пусть в ∆ABC на сторонах BC,AC,AB или их продолжениях взяты
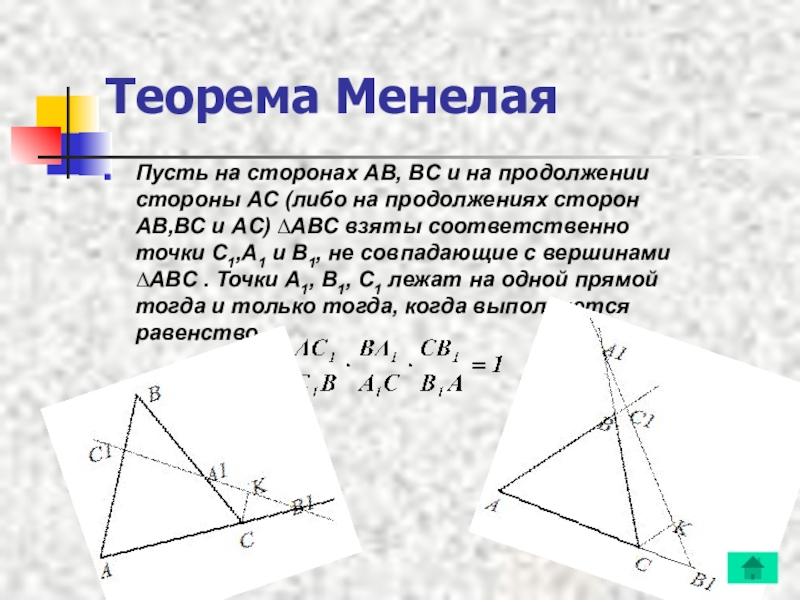
Слайд 3Теорема Менелая
Пусть на сторонах AB, BC и на продолжении стороны AC
Слайд 4Практическое применение теорем
1. Теорема Менелая и пропорциональные отрезки в треугольнике.
2. Теорема
3. Решение задач на пропорциональное деление отрезков в треугольнике.
4. Решение задач, связанных с нахождением площадей.
5. Комбинированные задачи.
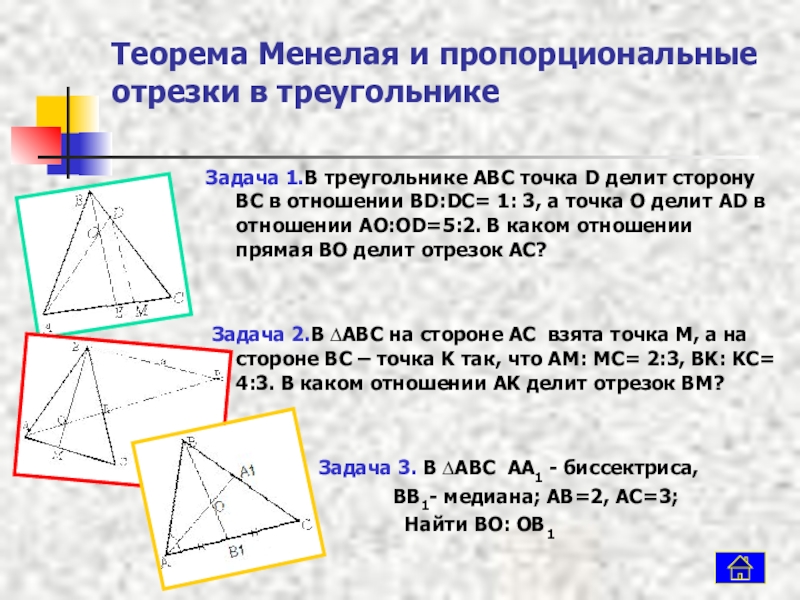
Слайд 5Теорема Менелая и пропорциональные отрезки в треугольнике
Задача 1.В треугольнике ABC точка
Задача 2.В ∆ABC на стороне AC взята точка M, а на стороне BC – точка K так, что AM: MC= 2:3, BK: KC= 4:3. В каком отношении AK делит отрезок BM?
Задача 3. В ∆ABC AA1 - биссектриса,
BB1- медиана; AB=2, AC=3;
Найти BO: OB1
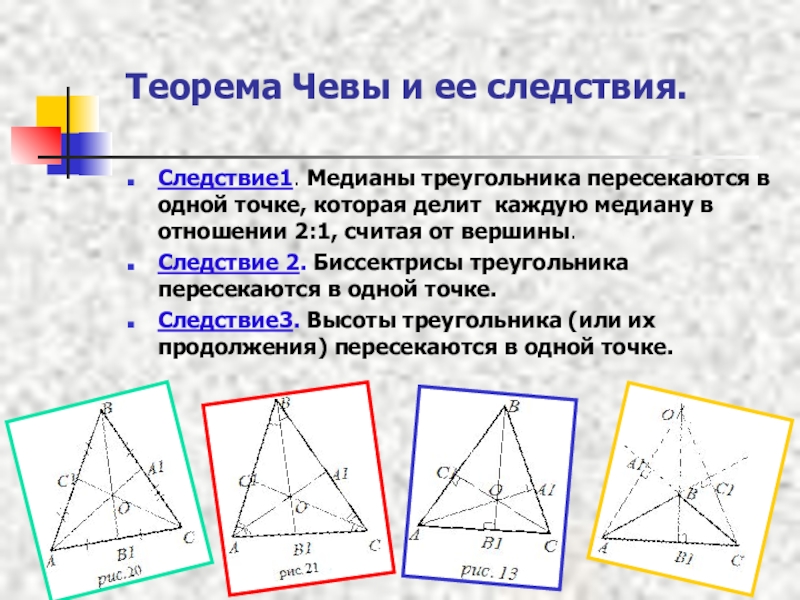
Слайд 6Теорема Чевы и ее следствия.
Следствие1. Медианы треугольника пересекаются в одной
Следствие 2. Биссектрисы треугольника пересекаются в одной точке.
Следствие3. Высоты треугольника (или их продолжения) пересекаются в одной точке.
Слайд 7Теорема Чевы и ее следствия.
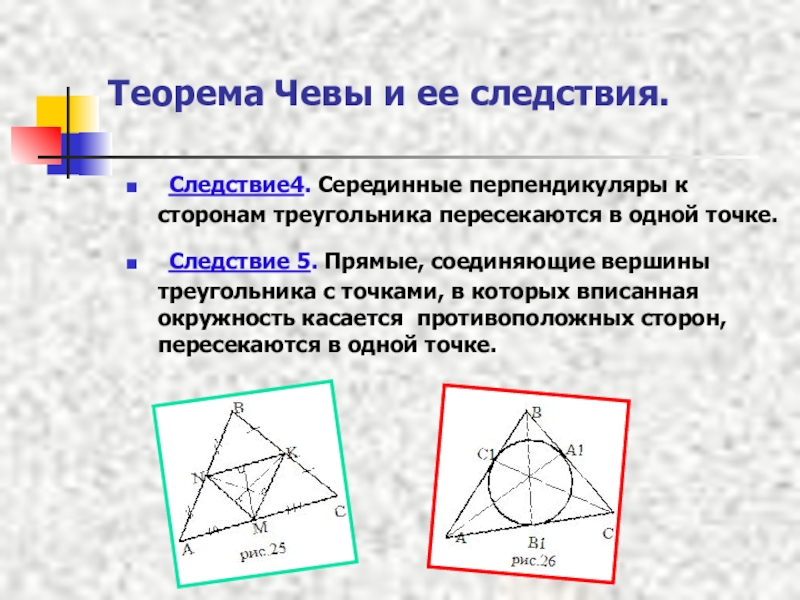
Следствие4. Серединные перпендикуляры к сторонам
Следствие 5. Прямые, соединяющие вершины треугольника с точками, в которых вписанная окружность касается противоположных сторон, пересекаются в одной точке.
Слайд 8Применение теорем Чевы и Менелая к задачам на доказательство
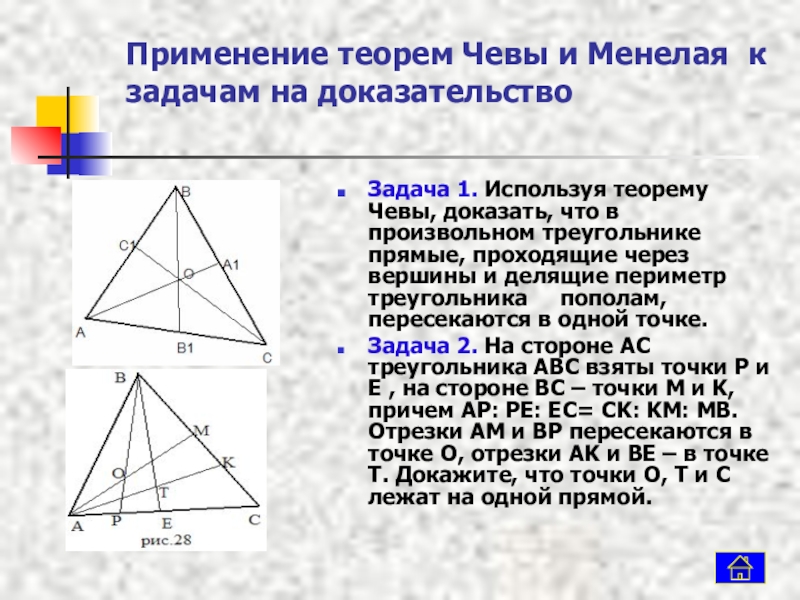
Задача 1. Используя
Задача 2. На стороне AC треугольника ABC взяты точки P и E , на стороне BC – точки M и K, причем AP: PE: EC= CK: KM: MB. Отрезки AM и BP пересекаются в точке O, отрезки AK и BE – в точке T. Докажите, что точки O, T и С лежат на одной прямой.
Слайд 9Задачи на пропорциональное деление отрезков в треугольнике.
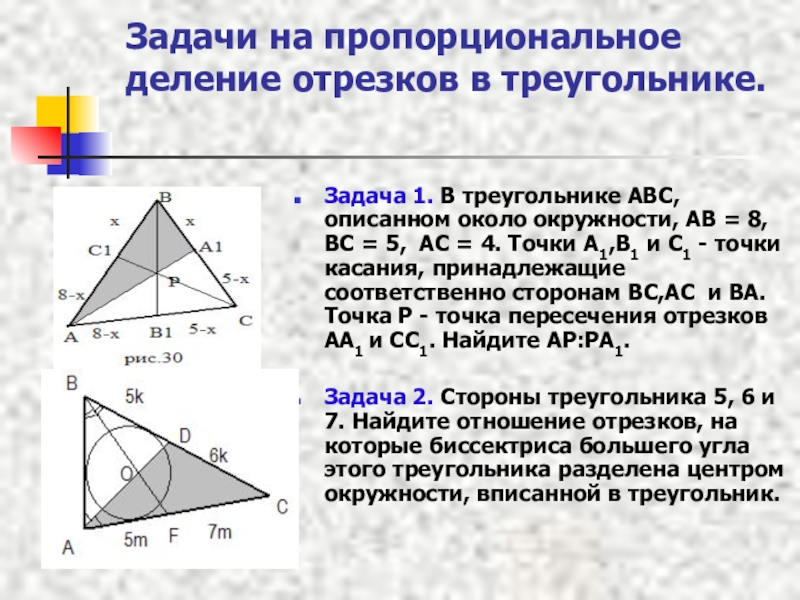
Задача 1. В треугольнике ABC,
Задача 2. Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.
Слайд 10Задачи на пропорциональное деление отрезков в треугольнике.
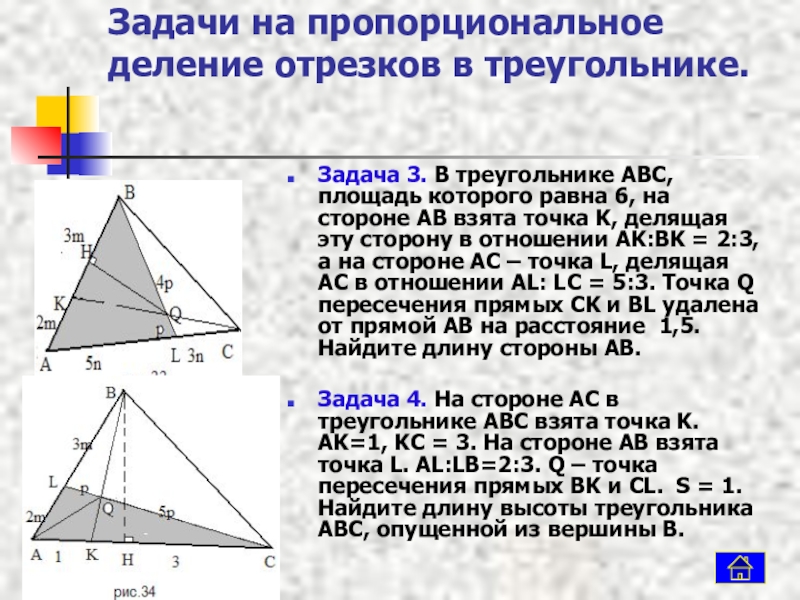
Задача 3. В треугольнике ABC,
Задача 4. На стороне AC в треугольнике ABC взята точка K. AK=1, KC = 3. На стороне AB взята точка L. AL:LB=2:3. Q – точка пересечения прямых BK и CL. S = 1. Найдите длину высоты треугольника ABC, опущенной из вершины B.
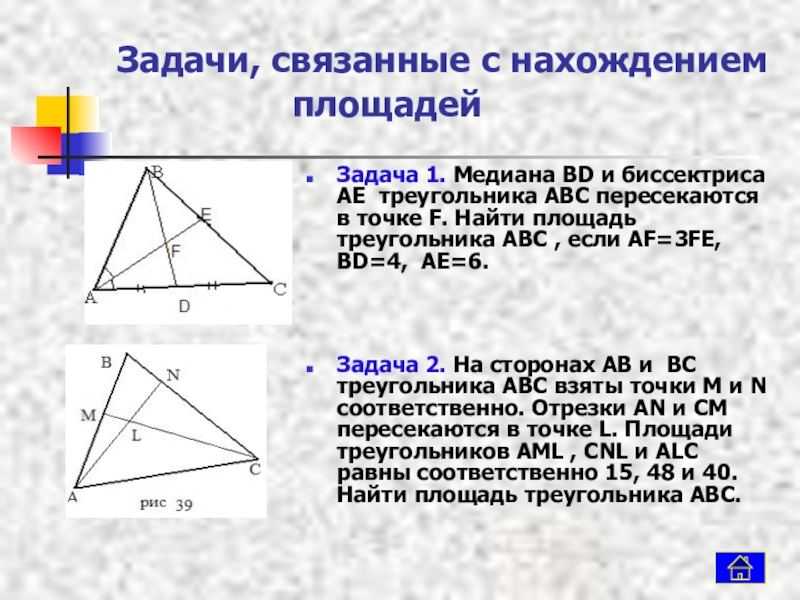
Слайд 11 Задачи, связанные с нахождением
Задача 1. Медиана BD и биссектриса AE треугольника ABC пересекаются в точке F. Найти площадь треугольника ABC , если AF=3FE, BD=4, AE=6.
Задача 2. На сторонах AB и BC треугольника ABC взяты точки M и N соответственно. Отрезки AN и CM пересекаются в точке L. Площади треугольников AML , CNL и ALC равны соответственно 15, 48 и 40. Найти площадь треугольника ABC.
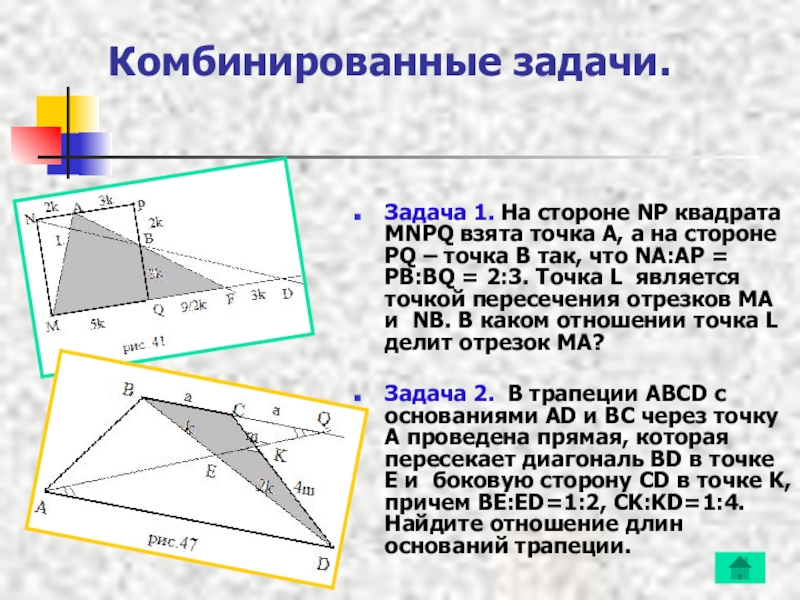
Слайд 12Комбинированные задачи.
Задача 1. На стороне NP квадрата MNPQ взята точка A,
Задача 2. В трапеции ABCD с основаниями AD и BC через точку A проведена прямая, которая пересекает диагональ BD в точке E и боковую сторону CD в точке K, причем BE:ED=1:2, CK:KD=1:4. Найдите отношение длин оснований трапеции.
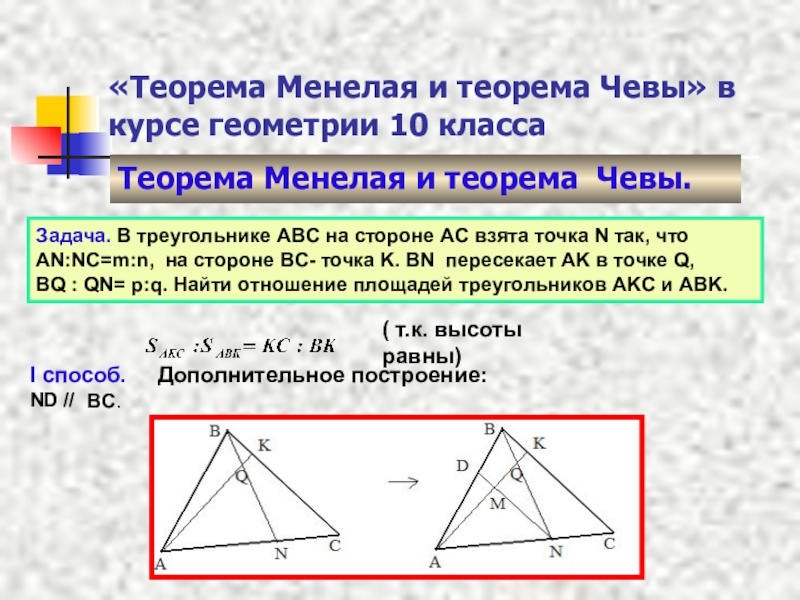
Слайд 13«Теорема Менелая и теорема Чевы» в курсе геометрии 10 класса
Теорема Менелая
Задача. В треугольнике ABC на стороне AC взята точка N так, что AN:NC=m:n, на стороне BC- точка K. BN пересекает AK в точке Q,
BQ : QN= p:q. Найти отношение площадей треугольников AKC и ABK.
( т.к. высоты равны)
I способ. Дополнительное построение: ND //
BC.
Слайд 15Задача. В равнобедренном треугольнике ABC (AС=BC) проведены медиана BN и высота
Решение: AN=NC, AM=5+2=7. Рассмотрим ∆AMC и секущую NB. По теореме Менелая
Пусть коэффициент пропорциональности равен k, тогда СМ=3k, BM=2k. Из ∆ACM- прямоугольного:
;
,
,
Ответ:
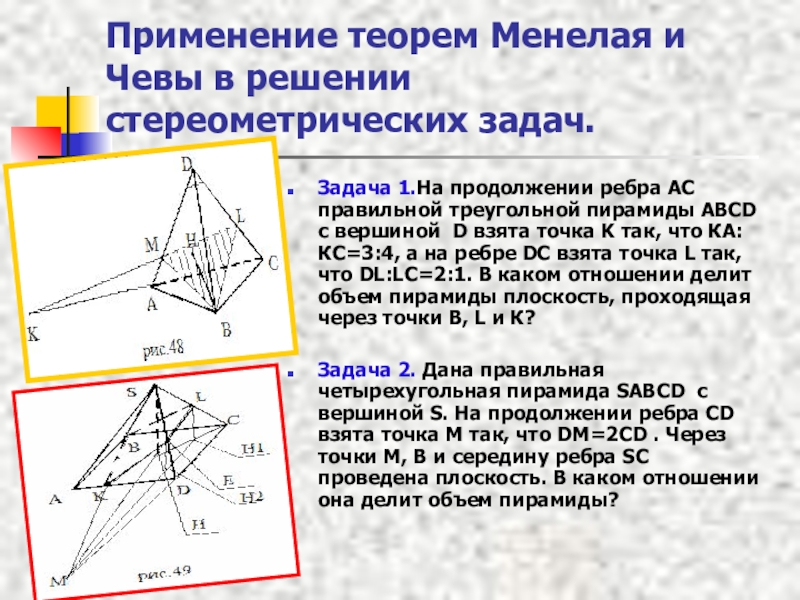
Слайд 16Применение теорем Менелая и Чевы в решении стереометрических задач.
Задача 1.На продолжении
Задача 2. Дана правильная четырехугольная пирамида SABCD с вершиной S. На продолжении ребра CD взята точка M так, что DM=2CD . Через точки М, В и середину ребра SC проведена плоскость. В каком отношении она делит объем пирамиды?
Слайд 17Применение теорем Менелая и Чевы в решении стереометрических задач.
Задача 3. Дана
Слайд 18 «Умение решать задачи- такое же практическое