- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Пифагора 8 класс
Содержание
- 1. Презентация по геометрии на тему Теорема Пифагора 8 класс
- 2. «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора»
- 3. Цели урока: обобщить знания по данной теме;проверить
- 4. «Квадрат, построенный на гипотенузе прямо-угольного треугольника, равновелик
- 5. ИСТОРИЧЕСКАЯ СПРАВКА Пифагор (Pythagoras) Самосский (ок. 570
- 6. Немного о Пифагоре
- 7. Школа Пифагора и пифагорейцыШкола существовала в период
- 8. Пентаграмма
- 9. Пифагоровы тройки
- 10. Практическое применение:В древнем Египте
- 11. НЕКОТОРЫЕ СПОСОБЫ ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ
- 12. Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах. Доказательство Пифагора
- 13. Доказательство теоремы Дано: прямоугольный треугольник
- 14. Доказательство теоремы Пифагора учащиеся средних веков считали
- 15. Устная работа Задача № 1 Найдите
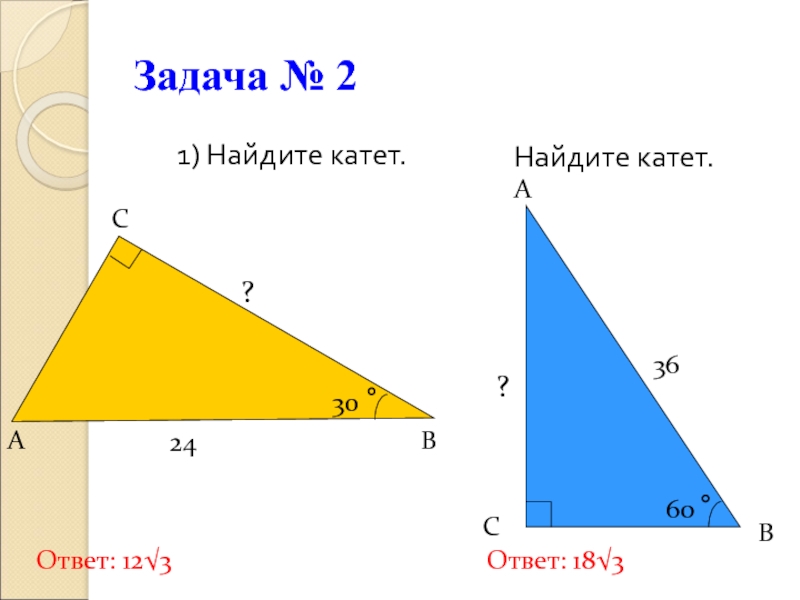
- 16. Задача № 2 1) Найдите
- 17. Задача № 3 Найдите сторону прямоугольника.
- 18. Зрительная гимнастика
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Самостоятельная работа№1. Катеты 8 и 15 см.
- 26. ВСA153х4х(3х)2 + (4х)2 = 1529х2 + 16х2
- 27. На берегу реки рос тополь одинокий.
- 28. Решение. Пусть CD – высота ствола.BD =
- 29. Древнеиндийская задача: Над озером тихимС полфута размеромВысился
- 30. Решение: Выполним чертёж к задаче и обозначим
- 31. Заповеди
- 32. Заповеди пифагорейцев: Делать то, что впоследствии не огорчит
- 33. Не закрывай глаза, когда хочется спать, не разобравши всех своих поступков в прошлый день.
- 34. Главная заповедь:«Сыщи себе верного друга, имея его , ты можешь обойтись без богов»
- 35. Памятник Пифагору находится в порту города Пифагорио
- 36. Пифагор придумал специальную
- 37. Кружка Пифагора выглядит как обычная кружка для
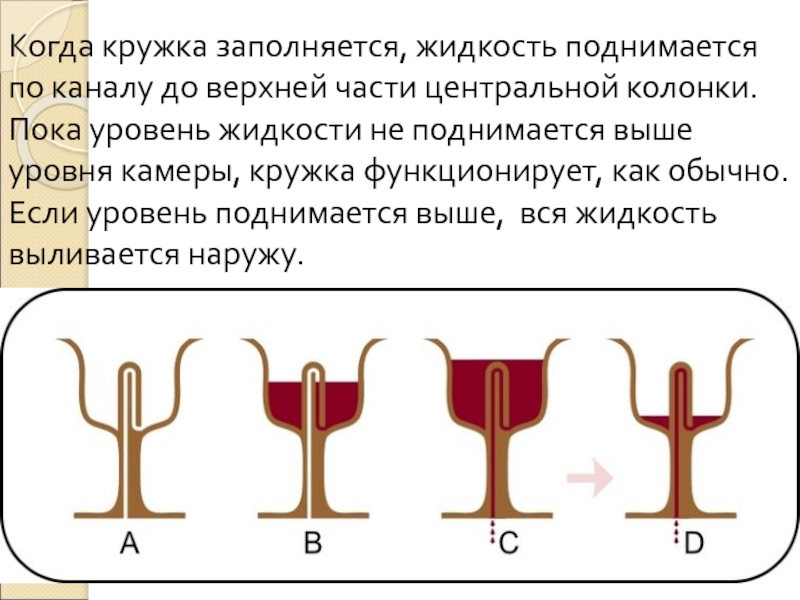
- 38. Когда кружка заполняется, жидкость
Слайд 3Цели урока:
обобщить знания по данной теме;
проверить навык решения задач с помощью
познакомить учащихся с некоторыми фактами из биографии Пифагора;
рассмотреть способ доказательства теоремы;
формировать познавательный интерес;
совершенствовать приёмы устных вычислений.
Слайд 4
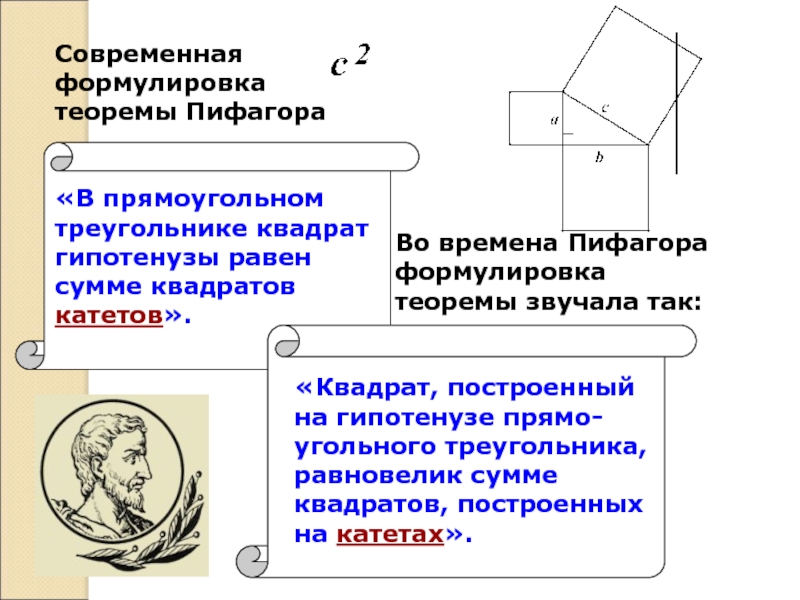
«Квадрат, построенный на гипотенузе прямо-угольного треугольника, равновелик сумме квадратов, построенных на
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов катетов».
Во времена Пифагора формулировка теоремы звучала так:
Современная формулировка
теоремы Пифагора
Слайд 5ИСТОРИЧЕСКАЯ СПРАВКА
Пифагор (Pythagoras) Самосский
(ок. 570 - 500 до н.э.)
Пифагор жил в 6 веке до н. э.
В молодости он много путешествовал, собирая по крупицам знания древнейших народов по математике, астрономии, технике.
Вернувшись на родину, на остров Самос, он собирает вокруг себя юношей и ведёт с ними беседы.
Так образовался «пифагорейский союз».
В союзе царит дисциплина, послушание. Слово учителя закон. Вскоре союз становится политическим союзом единомышленников.
Слайд 6Немного о Пифагоре
Пифагор-это не имя,
то , что он высказывал истину также постоянно, как аракул
(«Пифагор» значит
«убеждающий речью»).
Слайд 7Школа Пифагора и пифагорейцы
Школа существовала в период с 585 до 400
Эта школа заложила основу греческой арифметики, которая ограничивалась изучением целых чисел.
Их арифметика геометрична, она разбивает числа в зависимости от формы соответствующих им фигур из точек на треугольные, квадратные, пятиугольные и т.д.
Попасть в школу было не просто. Претендент должен был выдержать ряд испытаний, одним из таких испытаний являлся обет пятилетнего молчания.
Законом организации было хранение тайны, несоблюдение которой строго каралось – вплоть до смерти.
Слайд 9 Пифагоровы тройки
Используя теорему, Пифагор
a2+b2 = c2
32+42=52
9+16=25
25=25
Слайд 10 Практическое применение:
В древнем Египте после разлива Нила требовалось
Правильно ли они поступали? Ответ обоснуйте.
Слайд 12
Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на
Доказательство Пифагора
Слайд 13
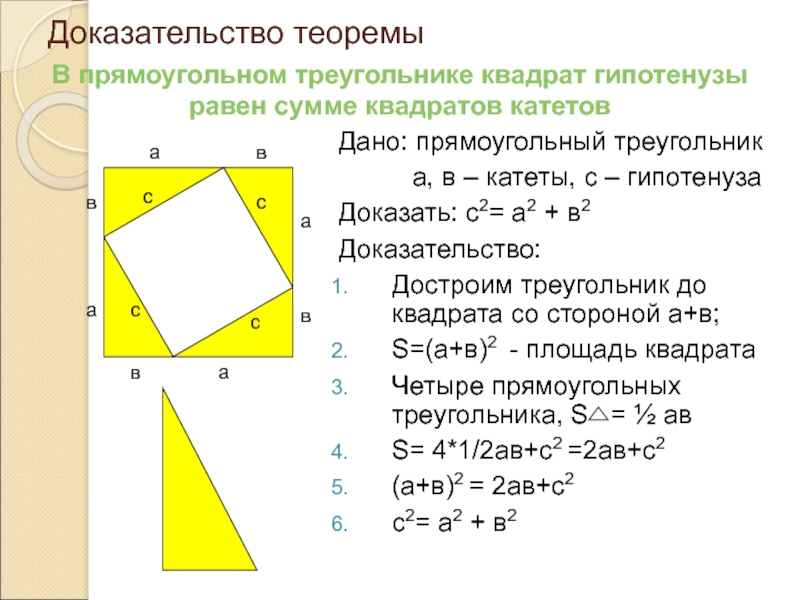
Доказательство теоремы
Дано: прямоугольный треугольник
а, в
Доказать: с2= а2 + в2
Доказательство:
Достроим треугольник до квадрата со стороной а+в;
S=(а+в)2 - площадь квадрата
Четыре прямоугольных треугольника, S = ½ ав
S= 4*1/2ав+с2 =2ав+с2
(а+в)2 = 2ав+с2
с2= а2 + в2
а
а
а
а
с
с
с
с
в
в
в
в
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 14Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли
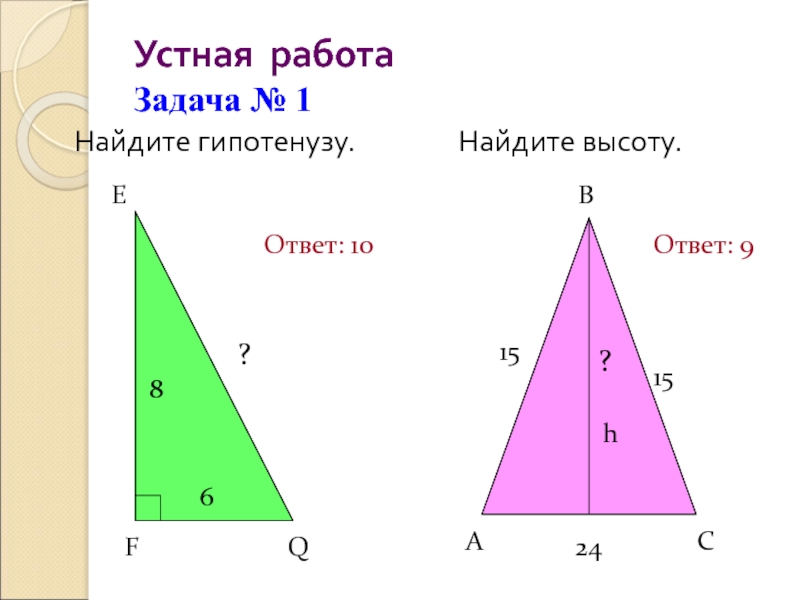
Слайд 15Устная работа
Задача № 1
Найдите гипотенузу.
Найдите высоту.
E
F
Q
8
6
?
B
A
C
15
15
24
?
h
Ответ: 10
Ответ: 9
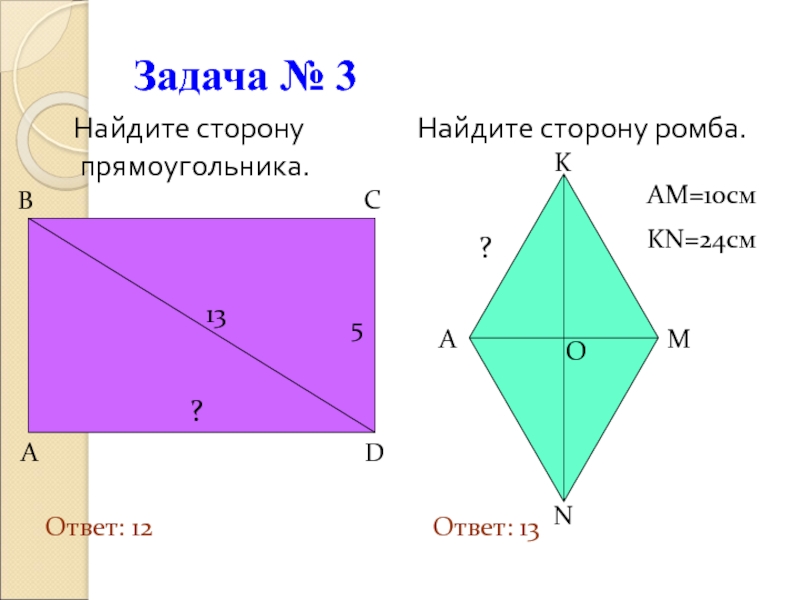
Слайд 17Задача № 3
Найдите сторону прямоугольника.
Найдите сторону ромба.
13
5
A
D
B
C
O
K
A
M
N
?
AM=10см
KN=24см
Ответ: 12 Ответ: 13
Слайд 25Самостоятельная работа
№1. Катеты 8 и 15 см. Найти гипотенузу
№2. Гипотенуза 61
№3. Диагональ прямоугольника 15 см, одна из сторон – 9 см. Найти его периметр
№4. Катеты прямоугольного треугольника относятся как 3 : 4, а гипотенуза равна 15 см. Найдите периметр треугольника.
№5. Катет прямоугольного треугольника равен 5 см , а медиана, проведенная к другому катету равна 13см. Найдите гипотенузу прямоугольного треугольника.
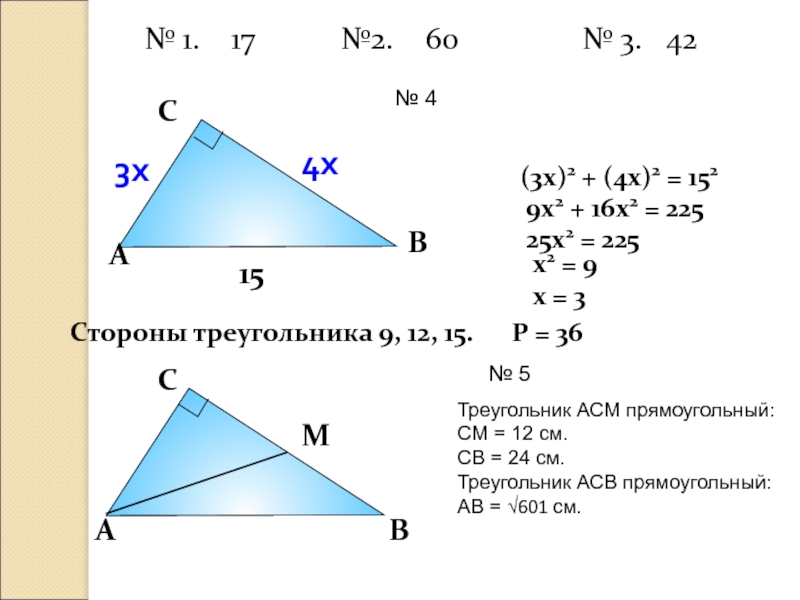
Слайд 26
В
С
A
15
3х
4х
(3х)2 + (4х)2 = 152
9х2 + 16х2 = 225
25х2 = 225
х2
х = 3
Стороны треугольника 9, 12, 15. Р = 36
№ 1. 17 №2. 60 № 3. 42
№ 4
№ 5
С
A
В
М
Треугольник АСМ прямоугольный:
СМ = 12 см.
СВ = 24 см.
Треугольник АСВ прямоугольный:
АВ = √601 см.
Слайд 27 На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол
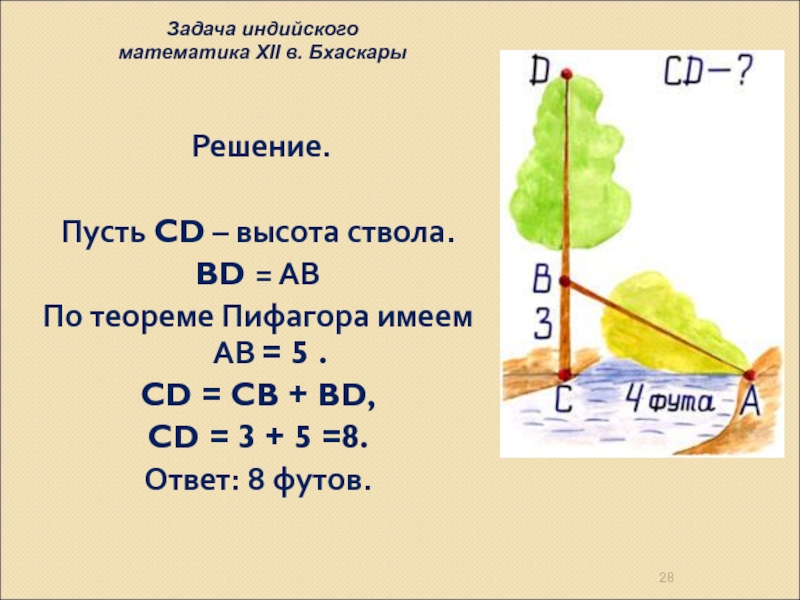
Задача индийского
математика XII в. Бхаскары
Слайд 28 Решение.
Пусть CD – высота ствола.
BD = АВ
По теореме Пифагора имеем
CD = CB + BD,
CD = 3 + 5 =8.
Ответ: 8 футов.
Задача индийского
математика XII в. Бхаскары
Слайд 29Древнеиндийская задача:
Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос одиноко,
И
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”
1фут = 0,3 м
Слайд 30 Решение:
Выполним чертёж к задаче и обозначим глубину озера АВ =Х,
Из треугольника ACB по теореме Пифагора имеем
AС2 – AВ2 = BC2,
(Х + 0,5)2 – Х2 = 22 ,
Х2 + Х + 0,25 – Х2 = 4,
Х = 3,75.
Таким образом, глубина озера составляет 3,75 фута.
3, 75 • 0,3 = 1,125 (м)
Ответ: 3,75 фута или 1, 125 м.
Древнеиндийская задача:
Слайд 31
Заповеди Пифагора
Вот они!
Слайд 32Заповеди пифагорейцев:
Делать то, что впоследствии не огорчит тебя и не заставит
Не делай никогда того, что не знаешь, но научись всему, что следует знать;
Не пренебрегай здоровьем своего тела;
Приучайся жить просто и без роскоши.