- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Сложение и вычитание векторов ( 9 класс)
Содержание
- 1. Презентация по геометрии на тему Сложение и вычитание векторов ( 9 класс)
- 2. Сложение векторов по правилу треугольникаДаны векторы a
- 3. Сложение векторов по правилу параллелограммаДаны векторы a
- 4. Сложение нескольких векторов по правилу многоугольникаСумму нескольких
- 5. Теория:Чтобы лучше понять закон вычитания векторов, нужно
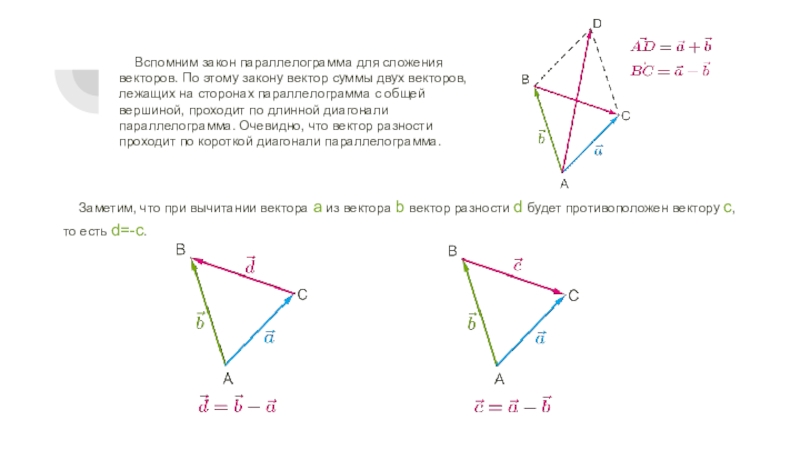
- 6. Вспомним закон параллелограмма для сложения векторов. По
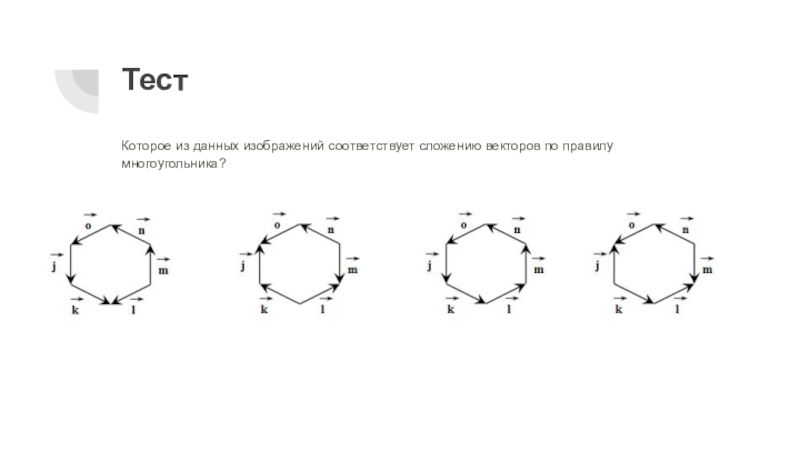
- 7. ТестКоторое из данных изображений соответствует сложению векторов по правилу многоугольника?
- 8. Даны векторы g и h. На каком
- 9. Спасибо за внимание
Слайд 2Сложение векторов по правилу треугольника
Даны векторы a и b. Если векторы
c
a
b
a+b=c
Такой приём сложения векторов называется правилом треугольника.
Слайд 3Сложение векторов по правилу параллелограмма
Даны векторы a и b. Если векторы
d
a
c
a+b=c.
Такой приём сложения векторов называется правилом параллелограмма.
Так как a+b=c; выполняя сложение по правилу треугольника, убедимся, что суммой остаётся тот же вектор c. Поэтому оба способа сложения равноценны.
1. Для любых двух векторов a и b в силе равенство a+b=b+a (коммутативный, или переместительный, закон сложения).
2. Для любых трёх векторов a, b, c в силе равенство (a+b)+c=a+(b+c) (ассоциативный, или сочетательный, закон сложения).
Слайд 4Сложение нескольких векторов по правилу многоугольника
Сумму нескольких векторов получаем так: складываем
Из закона сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.
Такой приём сложения нескольких векторов называется правилом многоугольника.
a
b
c
d
e
a+b+c+d+e
Слайд 5Теория:
Чтобы лучше понять закон вычитания векторов, нужно вспомнить свойство математических действий:
Если x+y=z, то x=z−y.Такое же свойство справедливо и для действий с векторами.
Чтобы вычесть вектор b из вектора a, нужно найти такой вектор c, сумма которого с вектором b составляла бы вектор a
Обрати внимание!
Легче запомнить, как найти разность векторов a и b, следующим образом:
1) векторы нужно привести к общему началу A;
2) соединить конечные точки B и C;
3) отметить направление вектора разности от конечной точки уменьшителя к конечной точке уменьшаемого вектора.
Слайд 6Вспомним закон параллелограмма для сложения векторов. По этому закону вектор суммы
Заметим, что при вычитании вектора a из вектора b вектор разности d будет противоположен вектору c, то есть d=-c.