- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Шар и свера
Содержание
- 1. Презентация по геометрии на тему Шар и свера
- 2. Сфера и шар, так же как окружность
- 3. Шаром называется тело, которое состоит из всех
- 4. т.О – центр сферы;R – радиус сферы;АВ
- 5. Шар – тело вращения полукруга вокруг его диаметра как осиhttp://lapinagv.jimdo.com/
- 6. Сфера – тело вращения полуокружности вокруг его диаметра как осиhttp://lapinagv.jimdo.com/
- 7. Применение сферыhttp://lapinagv.jimdo.com/
- 8. Сферическая геометрия нужна не только астрономам, штурманам
- 9. Сечения шара плоскостью. Касательная плоскость.http://lapinagv.jimdo.com/
- 10. Теорема 1Всякое сечение шара плоскостью есть круг.
- 11. Плоскость, проходящая через центр шара, называется диаметральной
- 12. Теорема 2Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.http://lapinagv.jimdo.com/
- 13. ОпределениеПлоскость, проходящая через точку А шаровой поверхности
- 14. Теорема 3Касательная плоскость имеет с шаром только одну общую точку – точку касания.http://lapinagv.jimdo.com/
- 15. Теорема 4Через любую точку шаровой поверхности проходит
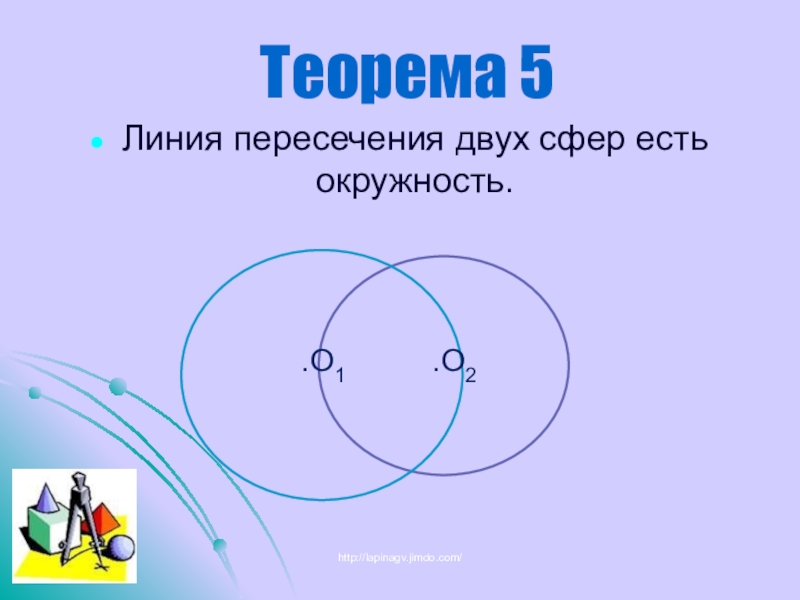
- 16. Теорема 5Линия пересечения двух сфер есть окружность.http://lapinagv.jimdo.com/
- 17. ЗадачаНайдите площадь сечения шара радиуса 41 см плоскостью, проведённой на расстоянии 29 см от центра шара.http://lapinagv.jimdo.com/
- 18. Площадь поверхности сферы, объём шара.http://lapinagv.jimdo.com/
- 19. Уравнение сферыПусть центр сферы в т. А(a,
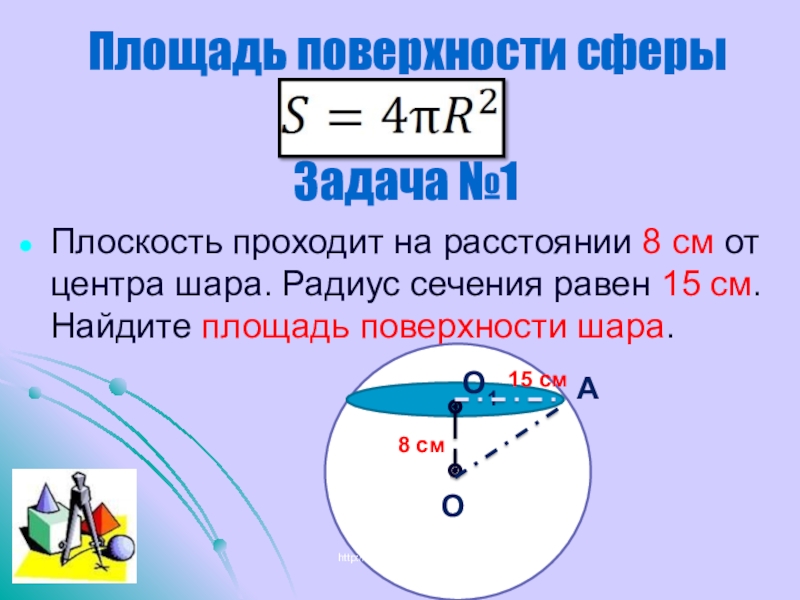
- 20. Площадь поверхности сферыЗадача №1Плоскость проходит на расстоянии
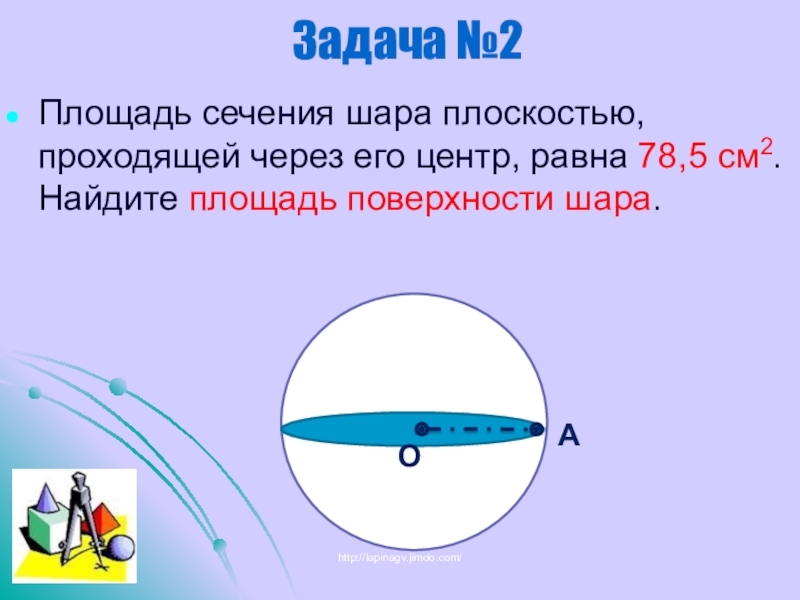
- 21. Площадь сечения шара плоскостью, проходящей через его центр, равна 78,5 см2. Найдите площадь поверхности шара.Задача №2http://lapinagv.jimdo.com/
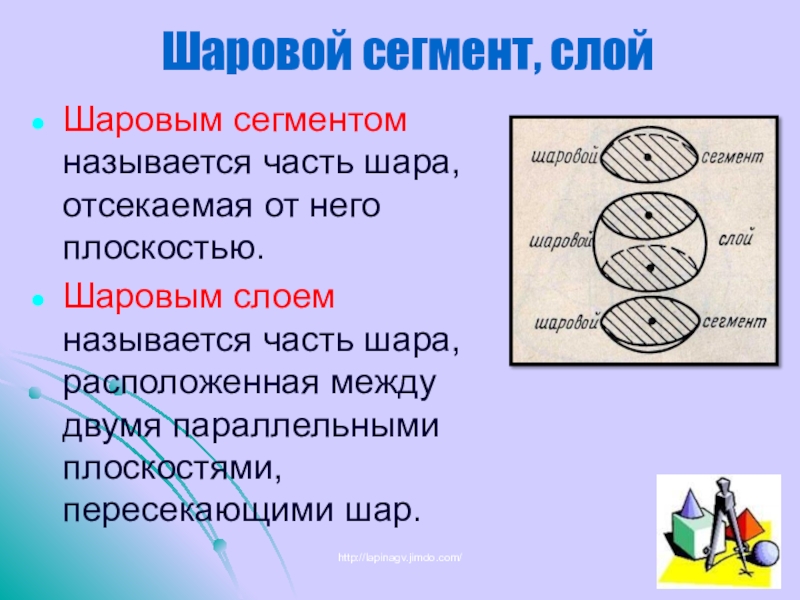
- 22. Шаровой сегмент, слойШаровым сегментом называется часть шара,
- 23. Шаровой секторШаровым сектором называется тело, которое получается из шарового сегмента и конуса.http://lapinagv.jimdo.com/
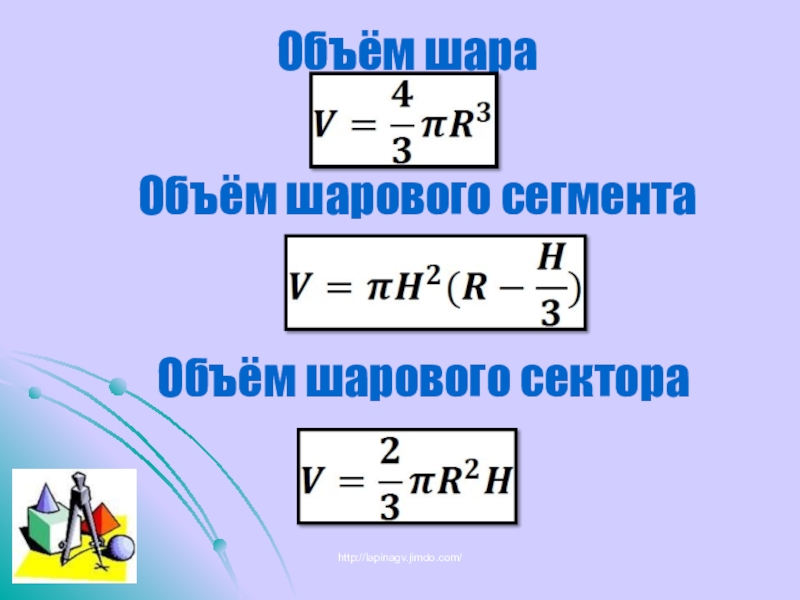
- 24. Объём шараОбъём шарового сегментаОбъём шарового сектораhttp://lapinagv.jimdo.com/
- 25. Архимед интерпретировал эти формулы так: объем и
- 26. Решение задач http://lapinagv.jimdo.com/
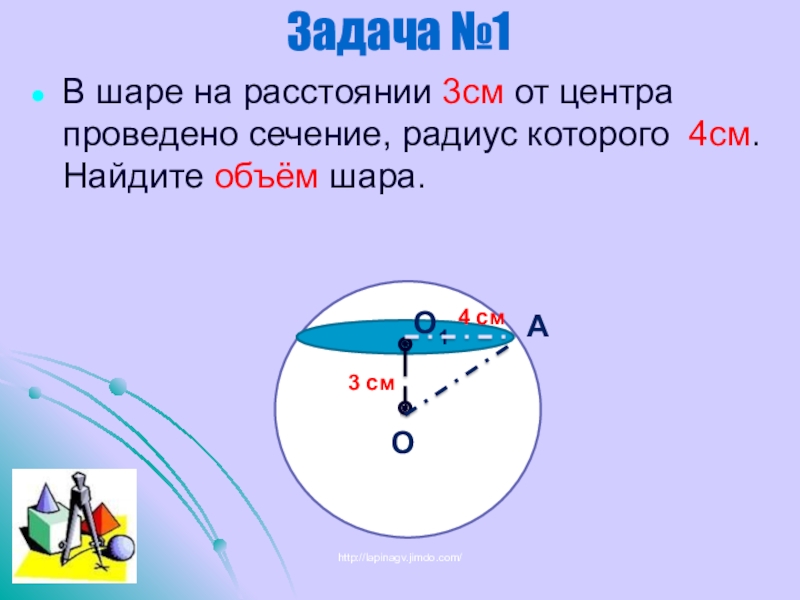
- 27. Задача №1В шаре на расстоянии 3см от центра проведено сечение, радиус которого 4см. Найдите объём шара.http://lapinagv.jimdo.com/
- 28. Площадь сечения шара плоскостью, проходящей через его
- 29. Шар с центром в точке О касается
- 30. Задача №5Объём шара равен
Слайд 2Сфера и шар, так же как окружность и круг, рассматривали еще
Открытие шарообразности Земли, появление представлений о небесной сфере дали толчок к развитию специальной науки – СФЕРИКИ, изучающей расположенные на сфере фигуры.
Автором первого сочинения о «сферике» был математик и астроном Евдокс Книдский (ок.408 – 355 до н.э.).
http://lapinagv.jimdo.com/
Слайд 3Шаром называется тело, которое состоит из всех точек пространства, находящихся на
Граница шара называется шаровой поверхностью или сферой.
Точками сферы являются все точки шара, удалённые от центра на расстояние, равное радиусу.
http://lapinagv.jimdo.com/
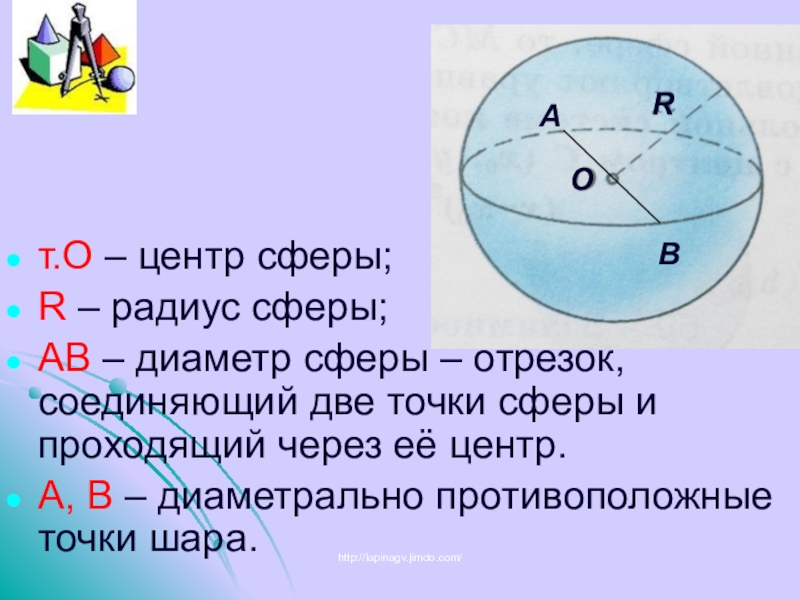
Слайд 4т.О – центр сферы;
R – радиус сферы;
АВ – диаметр сферы –
А, В – диаметрально противоположные точки шара.
http://lapinagv.jimdo.com/
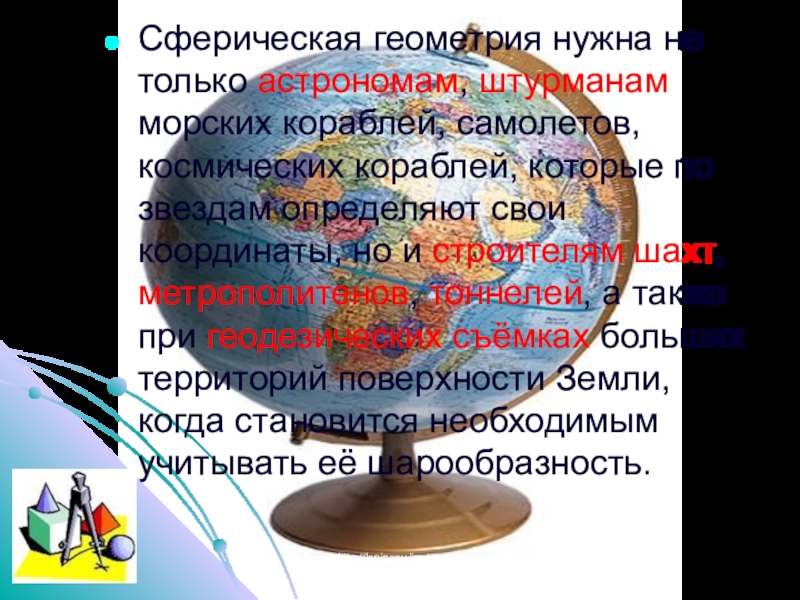
Слайд 8Сферическая геометрия нужна не только астрономам, штурманам морских кораблей, самолетов, космических
http://lapinagv.jimdo.com/
Слайд 10Теорема 1
Всякое сечение шара плоскостью есть круг. Центр этого круга есть
ОО' – перпендикуляр.
О' - центр круга –
основание перпендикуляра.
http://lapinagv.jimdo.com/
Слайд 11Плоскость, проходящая через центр шара, называется диаметральной плоскостью.
Сечение шара диаметральной плоскостью
Сечение шара
http://lapinagv.jimdo.com/
Слайд 12Теорема 2
Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара
http://lapinagv.jimdo.com/
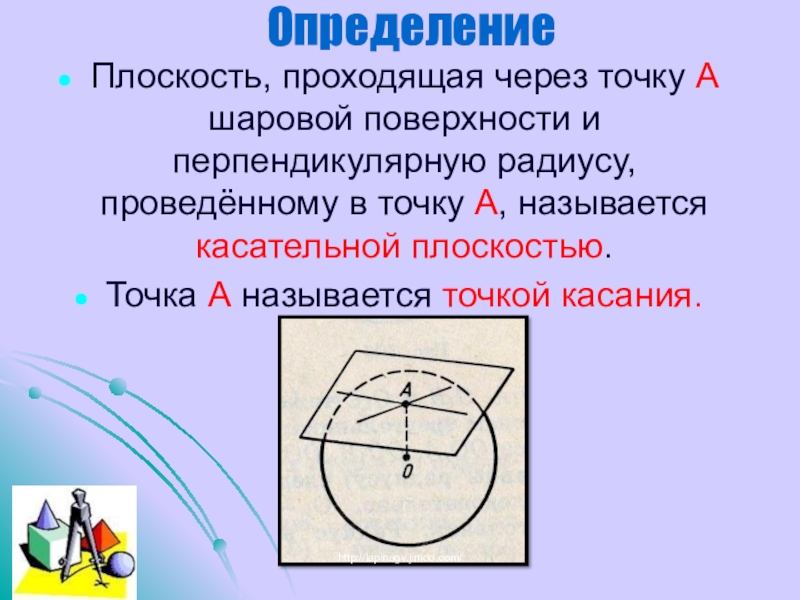
Слайд 13Определение
Плоскость, проходящая через точку А шаровой поверхности и перпендикулярную радиусу, проведённому
Точка А называется точкой касания.
http://lapinagv.jimdo.com/
Слайд 14Теорема 3
Касательная плоскость имеет с шаром только одну общую точку –
http://lapinagv.jimdo.com/
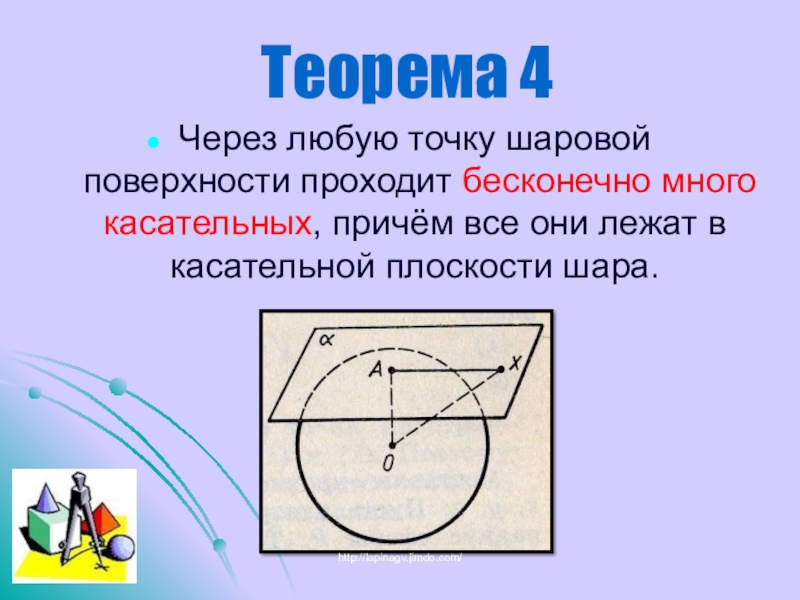
Слайд 15Теорема 4
Через любую точку шаровой поверхности проходит бесконечно много касательных, причём
http://lapinagv.jimdo.com/
Слайд 17Задача
Найдите площадь сечения шара радиуса 41 см плоскостью, проведённой на расстоянии
http://lapinagv.jimdo.com/
Слайд 19Уравнение сферы
Пусть центр сферы в т. А(a, b, c), радиус сферы
Квадрат расстояния от т. (x, y, z) до т. А:
(x-a)2 + (y-b)2 + (z-c)2=R2
Уравнение сферы с центром в начало координат:
x2 + y2 + z2=R2
http://lapinagv.jimdo.com/
Слайд 20Площадь поверхности сферы
Задача №1
Плоскость проходит на расстоянии 8 см от центра
http://lapinagv.jimdo.com/
Слайд 21Площадь сечения шара плоскостью, проходящей через его центр, равна 78,5 см2.
Задача №2
http://lapinagv.jimdo.com/
Слайд 22Шаровой сегмент, слой
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.
Шаровым
http://lapinagv.jimdo.com/
Слайд 23Шаровой сектор
Шаровым сектором называется тело, которое получается из шарового сегмента и
http://lapinagv.jimdo.com/
Слайд 25Архимед интерпретировал эти формулы так:
объем и поверхность шара составляют 2/3
Объем шара и площадь сферы.
http://lapinagv.jimdo.com/
Слайд 27Задача №1
В шаре на расстоянии 3см от центра проведено сечение, радиус
http://lapinagv.jimdo.com/
Слайд 28Площадь сечения шара плоскостью, проходящей через его центр, равна
Найдите
Задача №2
Задача №3
Площадь поверхности сферы равна
Вычислите объём соответствующего шара.
http://lapinagv.jimdo.com/
Слайд 29Шар с центром в точке О касается плоскости в точке А.
Задача №4
http://lapinagv.jimdo.com/
Слайд 30Задача №5
Объём шара равен
Задача №6
Сумма площадей поверхностей двух шаров радиуса 4 см равна площади поверхности некоторого большего шара. Каков объём этого большего шара?
http://lapinagv.jimdo.com/