г. Саратов
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Равнобедренный треугольник
Содержание
- 1. Презентация по геометрии на тему Равнобедренный треугольник
- 2. Девиз нашего урока: «Есть в математике нечто,вызывающее
- 3. «Развивать и тренировать своё геометрическое зрение»Кто ничего
- 4. Равнобедренный треугольник. Свойства равнобедренного треугольника
- 5. Повторение основных понятий Тест 1. Отрезок, соединяющий
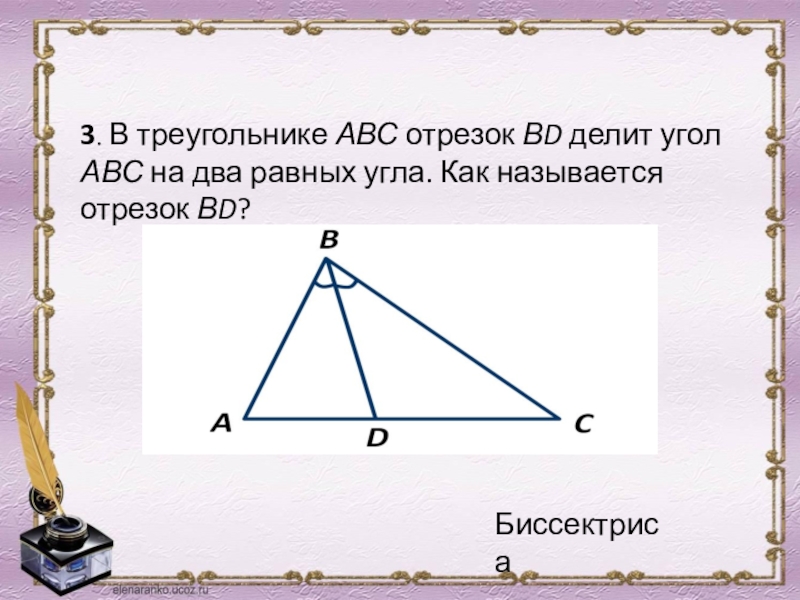
- 6. 3. В треугольнике АВС отрезок ВD делит
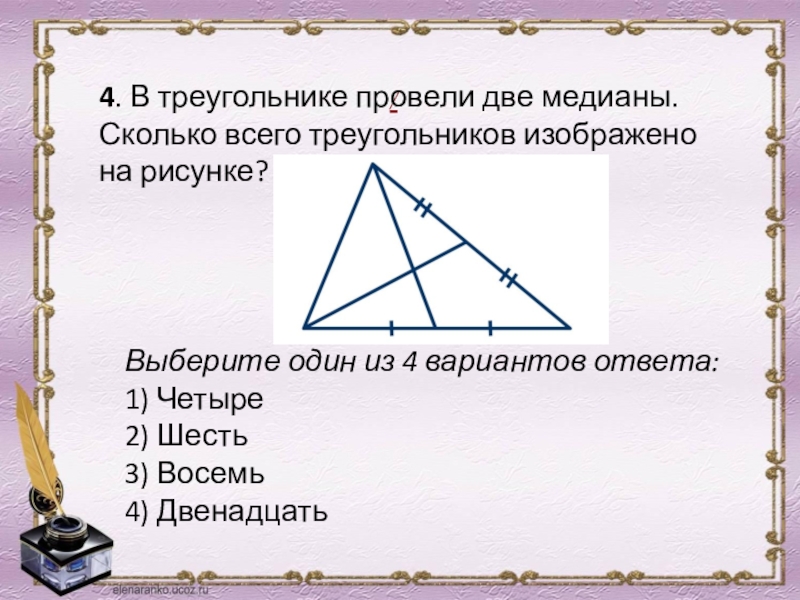
- 7. / 4. В треугольнике провели две
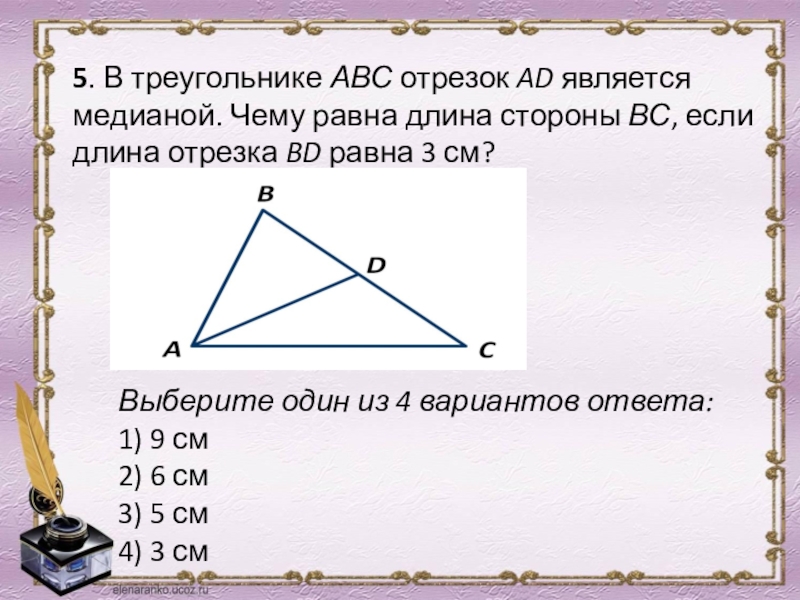
- 8. 5. В треугольнике АВС отрезок AD является
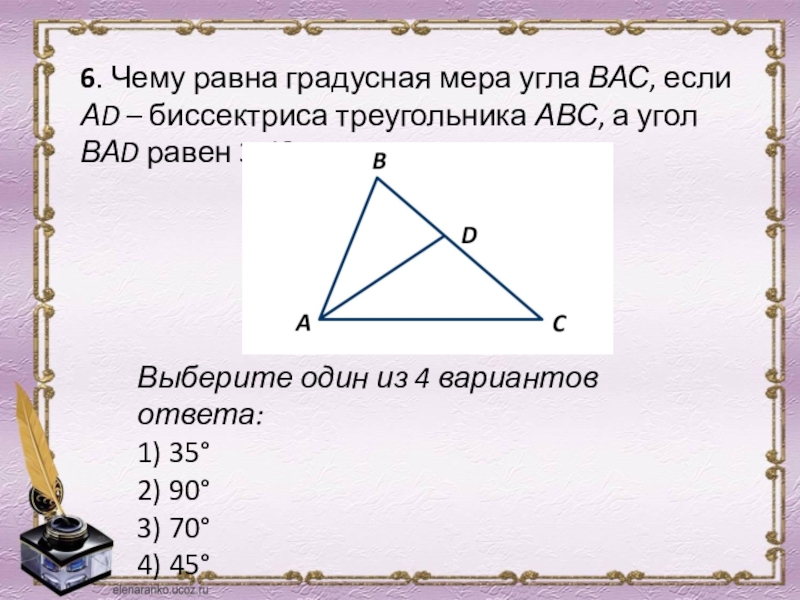
- 9. 6. Чему равна градусная мера
- 10. 7. Может ли точка пересечения
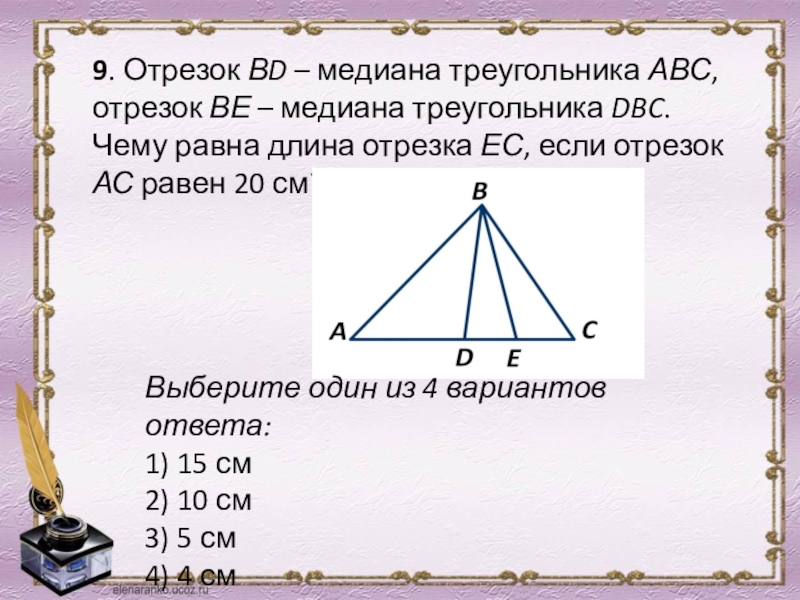
- 11. 9. Отрезок ВD – медиана
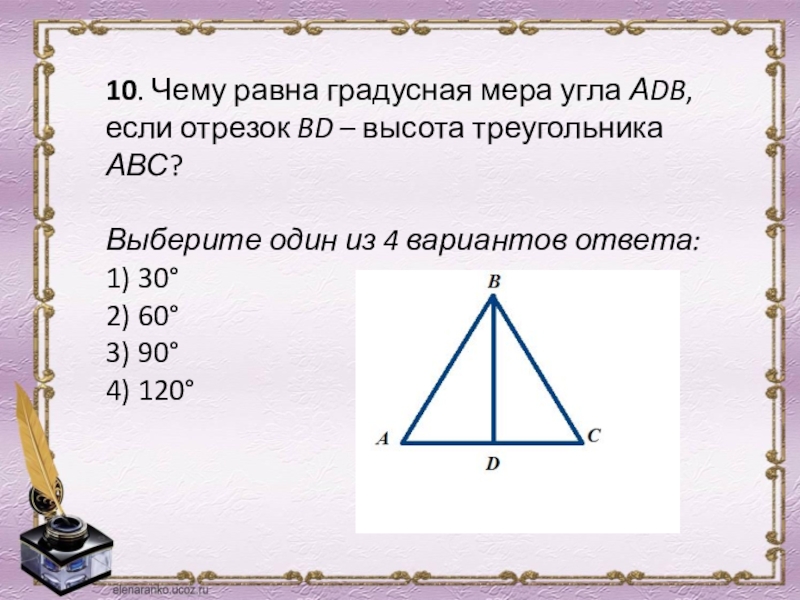
- 12. 10. Чему равна градусная мера
- 13. Объяснение нового материала Треугольник – самая простая замкнутая
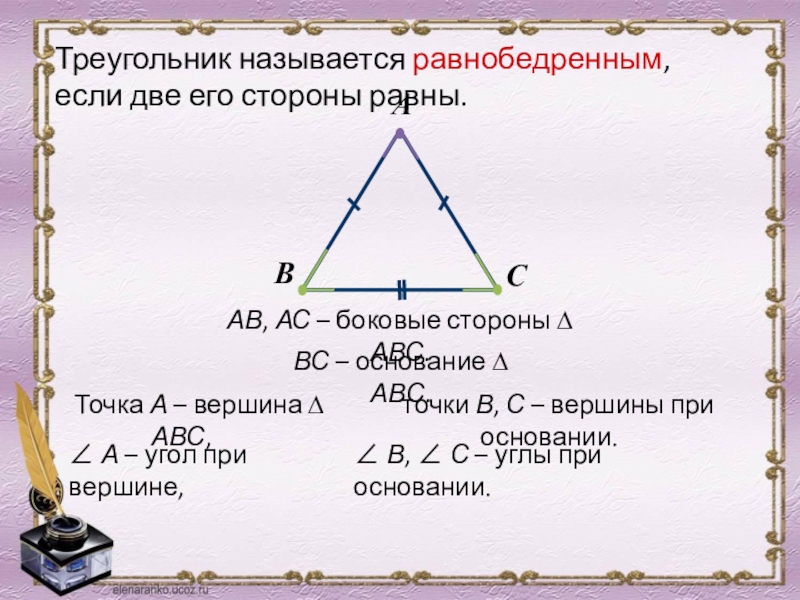
- 14. Треугольник называется равнобедренным, если две его стороны равны. АВ, АС – боковые стороны ∆ АВС.
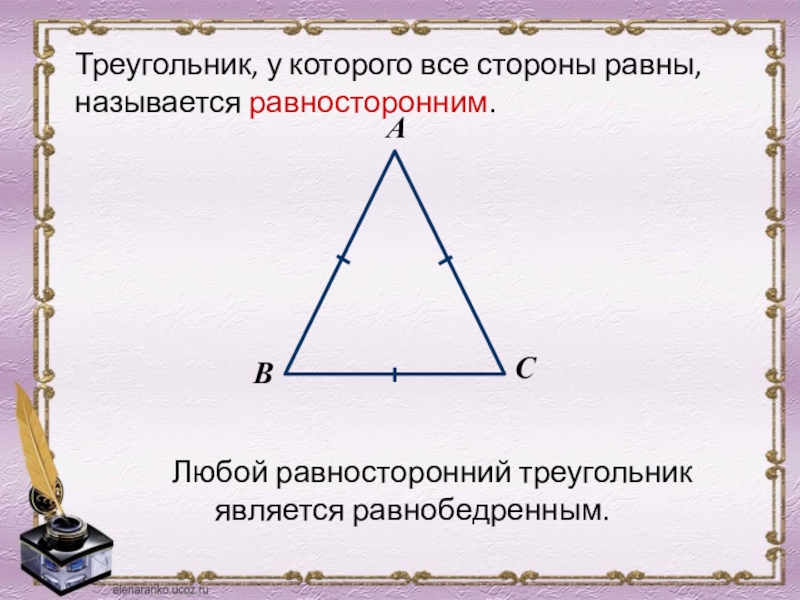
- 15. Любой равносторонний треугольник является равнобедренным.
- 16. Слайд 16
- 17. Теорема. В равнобедренном треугольнике углы при основании
- 18. Теорема. В равнобедренном треугольнике углы при основании
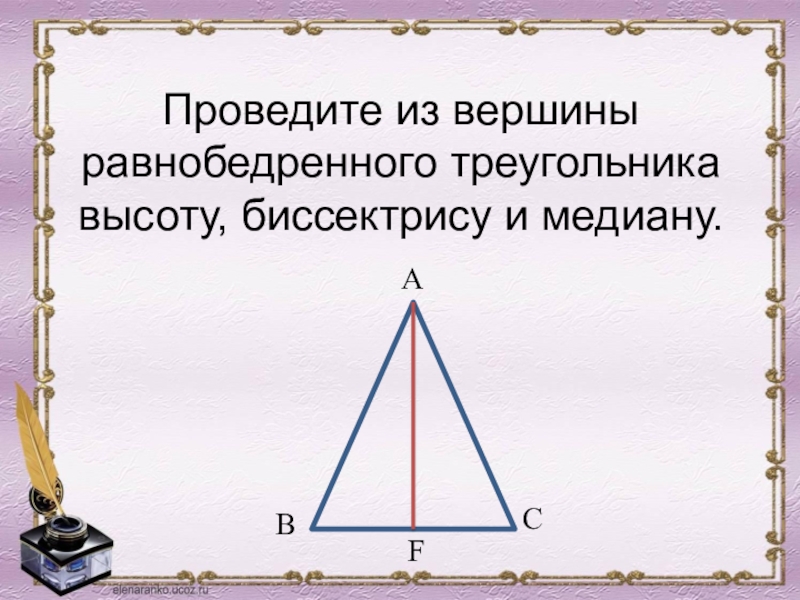
- 19. Проведите из вершины равнобедренного треугольника высоту, биссектрису и медиану. ABCF
- 20. Теорема. В равнобедренном треугольнике биссектриса, проведённая к
- 21. Высота равнобедренного треугольника, проведённая к основанию, является
- 22. Физминутка
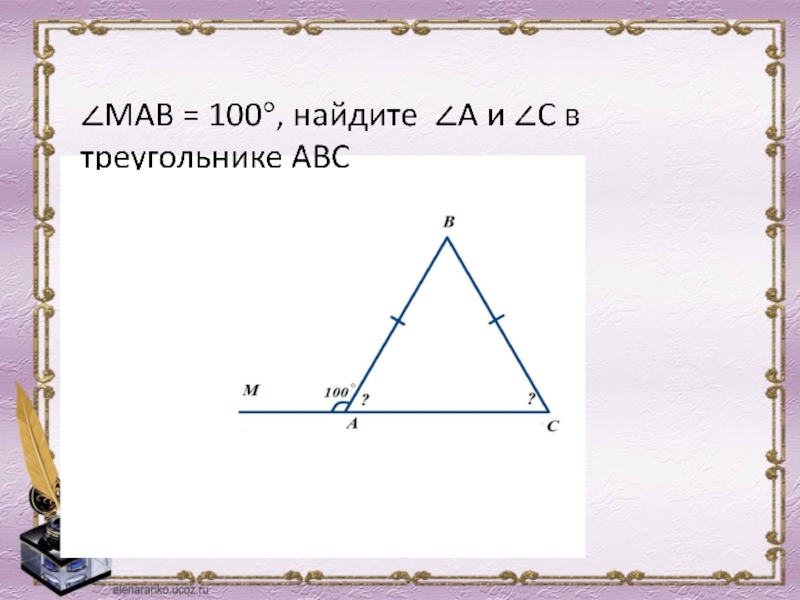
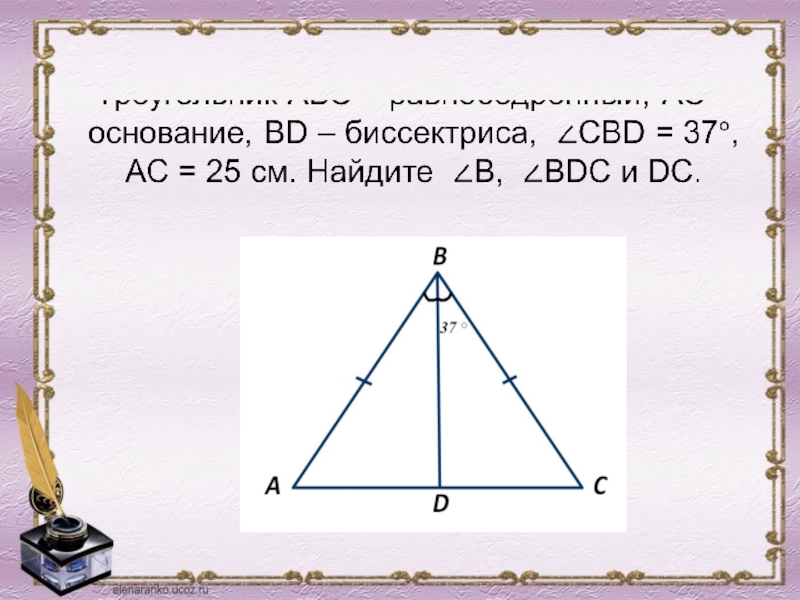
- 23. Какие из треугольников, изображённых на рисунке, являются
- 24. Слайд 24
- 25. Слайд 25
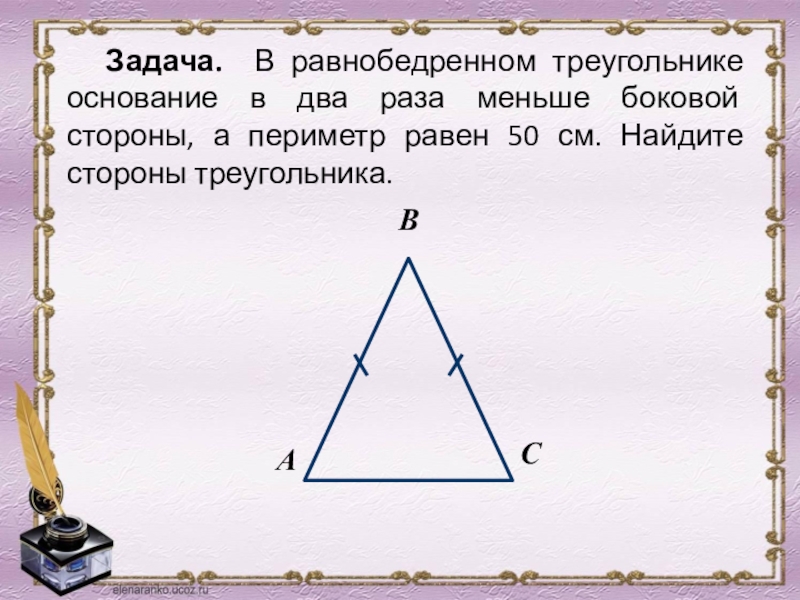
- 26. Задача. В равнобедренном треугольнике основание в два
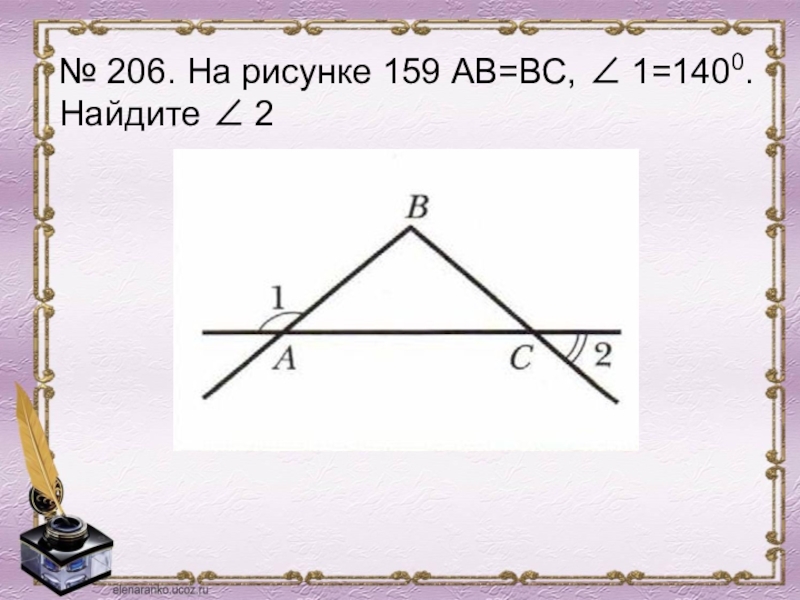
- 27. № 206. На рисунке 159 АВ=ВС, ∠ 1=1400. Найдите ∠ 2
- 28. Какой треугольник называется равнобедренным?Какой треугольник
- 29. Домашнее задание: п. 9, вопросы стр.63, № 108, 202, 205.
- 30. На уроке мне было все понятноЯ ничего не понялПонял, но затрудняюсь в решении задач
- 31. Спасибо за урок
Девиз нашего урока: «Есть в математике нечто,вызывающее восторг»На уроках геометрии очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур.
Слайд 1Равнобедренный треугольник.
Свойства равнобедренного треугольника
7 класс
Харитоненко Н.В. МОУ "Гимназия №89"
Слайд 2Девиз нашего урока:
«Есть в математике нечто,
вызывающее восторг»
На уроках геометрии очень
важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур.
Слайд 3«Развивать и тренировать своё геометрическое зрение»
Кто ничего не замечает,
Тот ничего не
изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.
Слайд 5Повторение основных понятий
Тест
1. Отрезок, соединяющий вершину треугольника с серединой
противолежащей стороны, называется ...
Медиана
2. Перпендикуляр, опущенный из вершины треугольника на противоположную сторону или её продолжение, называется ...
Высота
Медиана
2. Перпендикуляр, опущенный из вершины треугольника на противоположную сторону или её продолжение, называется ...
Высота
Слайд 63. В треугольнике АВС отрезок ВD делит угол АВС на два
равных угла. Как называется отрезок ВD?
Биссектриса
Слайд 7/
4. В треугольнике провели две медианы. Сколько всего треугольников
изображено на рисунке?
Выберите один из 4 вариантов ответа:
1) Четыре
2) Шесть
3) Восемь
4) Двенадцать
Слайд 85. В треугольнике АВС отрезок AD является медианой. Чему равна длина
стороны ВС, если длина отрезка BD равна 3 см?
Выберите один из 4 вариантов ответа:
1) 9 см
2) 6 см
3) 5 см
4) 3 см
Слайд 9
6. Чему равна градусная мера угла ВАС, если АD
– биссектриса треугольника АВС, а угол ВАD равен 35°?
Выберите один из 4 вариантов ответа:
1) 35°
2) 90°
3) 70°
4) 45°
Слайд 10
7. Может ли точка пересечения высот лежать вне треугольника?
Выберите
один из 2 вариантов ответа:
1) Может
2) Не может
1) Может
2) Не может
8. Сколько высот имеет любой треугольник?
Выберите один из 4 вариантов ответа:
1) Четыре
2) Одну
3) Две
4) Три
Слайд 11
9. Отрезок ВD – медиана треугольника АВС, отрезок ВЕ
– медиана треугольника DBC. Чему равна длина отрезка ЕС, если отрезок АС равен 20 см?
Выберите один из 4 вариантов ответа:
1) 15 см
2) 10 см
3) 5 см
4) 4 см
Слайд 12
10. Чему равна градусная мера угла АDB, если отрезок
BD – высота треугольника АВС?
Выберите один из 4 вариантов ответа:
1) 30°
2) 60°
3) 90°
4) 120°
Выберите один из 4 вариантов ответа:
1) 30°
2) 60°
3) 90°
4) 120°
Слайд 13Объяснение нового материала
Треугольник – самая простая замкнутая прямолинейная фигура, одна из
первых, свойства которой человек узнал ещё в глубокой древности.
Равнобедренный треугольник обладает рядом геометрических свойств, которые всегда имели широкое применение в практической жизни.
Выясним, какой треугольник называется равнобедренным, и какими свойствами он обладает.
Равнобедренный треугольник обладает рядом геометрических свойств, которые всегда имели широкое применение в практической жизни.
Выясним, какой треугольник называется равнобедренным, и какими свойствами он обладает.
Слайд 14Треугольник называется равнобедренным, если две его стороны равны.
АВ, АС –
боковые стороны ∆ АВС.
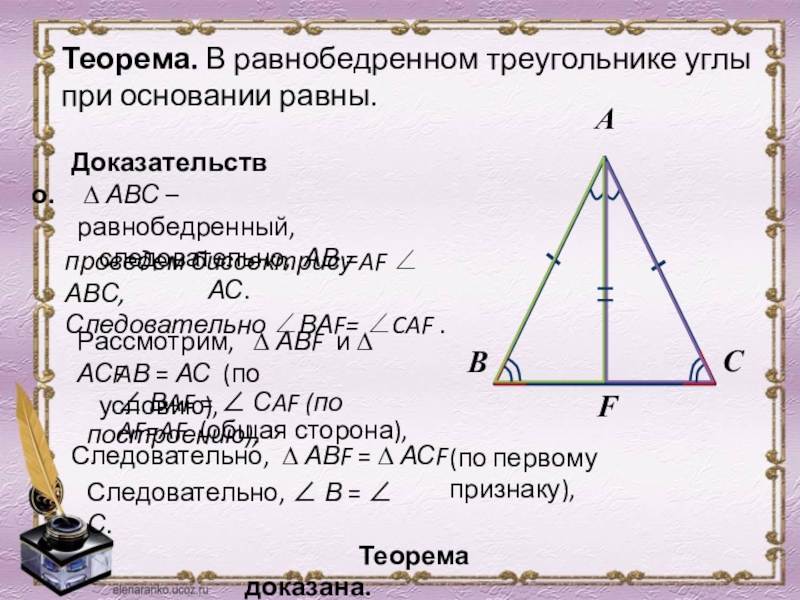
Слайд 17Теорема. В равнобедренном треугольнике углы при основании равны.
F
Дано
ΔАВС - равнобедренный
Док-ть:
∠ B = ∠ C
«Ни одно человеческое исследование не может назваться истинной наукой, если оно не прошло через математические доказательства»
Леонардо да Винчи
Слайд 18Теорема. В равнобедренном треугольнике углы при основании равны.
Доказательство.
AВ
= АС (по условию),
∠ ВAF = ∠ СAF (по построению),
Теорема доказана.
(по первому признаку),
Следовательно, ∆ АВF = ∆ АСF
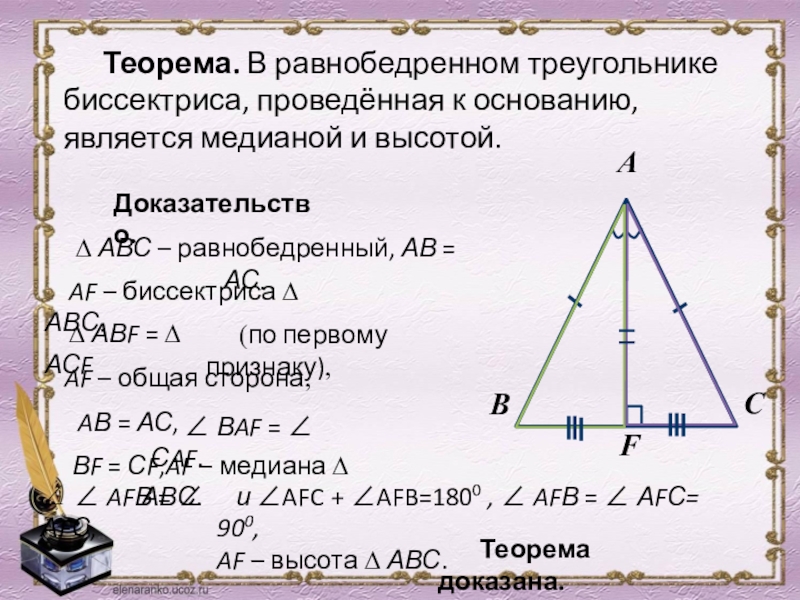
Слайд 20Теорема. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и
высотой.
Доказательство.
AВ = АС,
∠ ВAF = ∠ СAF.
AF – медиана ∆ АВС.
∠ ∠ AFВ = ∠ АFС,
и ∠AFC + ∠AFB=1800 , ∠ AFВ = ∠ АFС= 900,
AF – высота ∆ АВС.
Теорема доказана.
(по первому признаку),
Слайд 21Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.
Медиана равнобедренного
треугольника, проведённая к основанию, является высотой и биссектрисой.
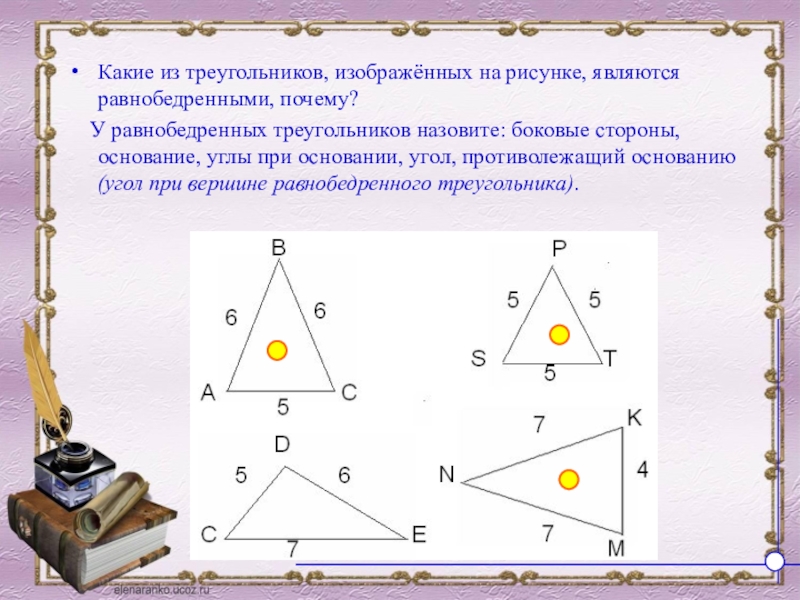
Слайд 23Какие из треугольников, изображённых на рисунке, являются равнобедренными, почему?
У
равнобедренных треугольников назовите: боковые стороны, основание, углы при основании, угол, противолежащий основанию (угол при вершине равнобедренного треугольника).
Слайд 26Задача. В равнобедренном треугольнике основание в два раза меньше боковой стороны,
а периметр равен 50 см. Найдите стороны треугольника.
Слайд 28
Какой треугольник называется равнобедренным?
Какой треугольник называется равносторонним?
Является ли равносторонний
треугольник равнобедренным?
Каким свойством обладают углы равнобедренного треугольника?
Каким свойством обладает биссектриса равнобедренного треугольника?
Любая ли биссектриса обладает этим свойством? Какая?
Любая ли биссектриса равностороннего треугольника обладает этим свойством?
