:
«Равнобедренный треугольник и его свойства»
учителя математики
ГБОУ школы №1056
Романенко Елены Алексеевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Равнобедренный треугольник и его свойства
Содержание
- 1. Презентация по геометрии на тему Равнобедренный треугольник и его свойства
- 2. РавнобедренныйЭто такой треугольник, у которого две стороны
- 3. Свойства равнобедренного треугольника
- 4. В равнобедренном треугольнике углы при основании равны. Дано:ΔABC - равнобедренныйДоказать:A = С
- 5. Доказательство:1) В ∆ABC из вершины B проведем
- 6. Биссектриса, проведенная к основанию в равнобедренном треугольнике
- 7. Доказательство:Рассмотрим ∆ABK и ∆CBKAB = BC (т.к.
- 8. РавностороннийТреугольник называют равносторонним, если у него все
- 9. Свойство равностороннего треугольника
- 10. У равностороннего треугольника градусная мера каждого угла
РавнобедренныйЭто такой треугольник, у которого две стороны равны. Равные стороны называются боковыми сторонами (бёдрами) треугольника, а третья сторона – основание.AC = CB AB – основание
Слайд 1Департамент образования города Москвы
Северо-Западное окружное управление образования
Презентация по геометрии на тему
Слайд 2Равнобедренный
Это такой треугольник, у которого две стороны равны. Равные стороны называются
боковыми сторонами (бёдрами) треугольника, а третья сторона – основание.
AC = CB
AB – основание
AC = CB
AB – основание
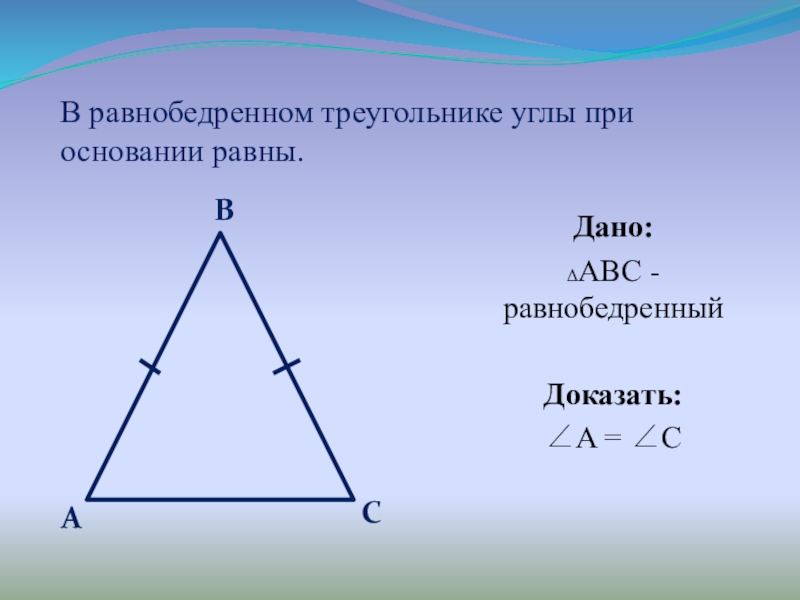
Слайд 4В равнобедренном треугольнике углы при основании равны.
Дано:
ΔABC - равнобедренный
Доказать:
A = С
Слайд 5Доказательство:
1) В ∆ABC из вершины B проведем биссектрису BD
Так
как BD – биссектриса, то ABD = CBD
2) AB = BC (по условию)
ABD = CBD (пункт 1) ∆ABD = ∆CBD (по I признаку)
BD – общая
3) Так как ∆ABD = ∆CBD, то A = C (как соответственные)
ч.т.д.
2) AB = BC (по условию)
ABD = CBD (пункт 1) ∆ABD = ∆CBD (по I признаку)
BD – общая
3) Так как ∆ABD = ∆CBD, то A = C (как соответственные)
ч.т.д.
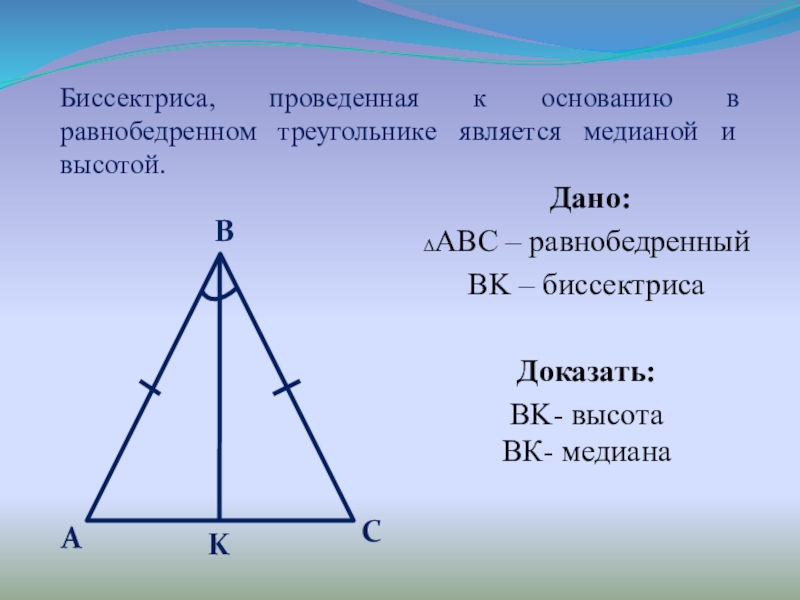
Слайд 6Биссектриса, проведенная к основанию в равнобедренном треугольнике является медианой и высотой.
Дано:
ΔАBС – равнобедренный
BK – биссектриса
Доказать:
BK- высота BК- медиана
ΔАBС – равнобедренный
BK – биссектриса
Доказать:
BK- высота BК- медиана
Слайд 7Доказательство:
Рассмотрим ∆ABK и ∆CBK
AB = BC (т.к. ∆ABC - равнобедренный)
AK =
KC (т.к. BK - медиана) ∆ABK = ∆CBK
BK – общая (по III признаку)
2) Так как ∆ABK = ∆CBK, то
AKB = CKB
AKB + CKB = 180° (как смежные) ∆ABK = ∆CBK = 90°,
а значит BK AC, то есть BK – высота
3) Так как ∆ABK = ∆CBK, то AKB = CKB, а значит BK – биссектриса
ч.т.д.
BK – общая (по III признаку)
2) Так как ∆ABK = ∆CBK, то
AKB = CKB
AKB + CKB = 180° (как смежные) ∆ABK = ∆CBK = 90°,
а значит BK AC, то есть BK – высота
3) Так как ∆ABK = ∆CBK, то AKB = CKB, а значит BK – биссектриса
ч.т.д.
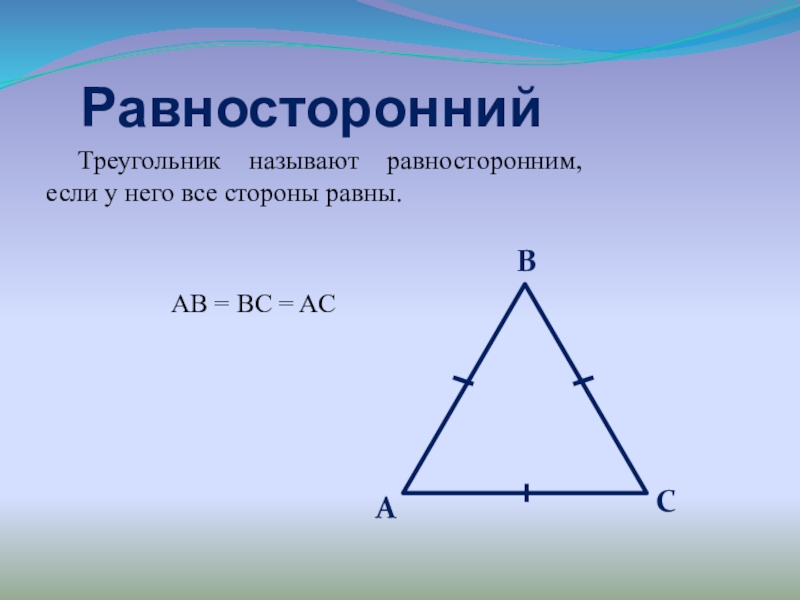
Слайд 8Равносторонний
Треугольник называют равносторонним, если у него все стороны равны.
AB = BC = AC
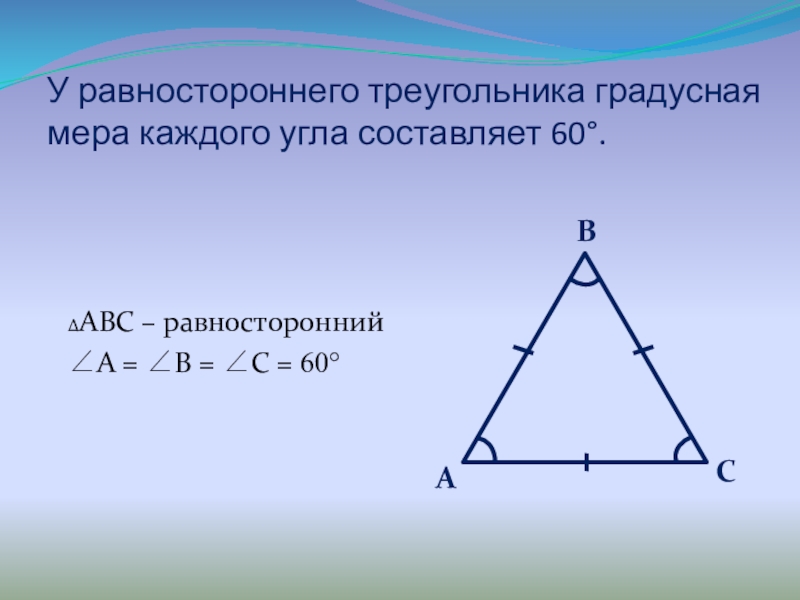
Слайд 10У равностороннего треугольника градусная мера каждого угла составляет 60.
ΔABC – равносторонний
A
= B = C = 60