- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Пирамида (11 класс)
Содержание
- 1. Презентация по геометрии на тему Пирамида (11 класс)
- 2. ПИРАМИДА
- 3. Содержание ОпределениеОпределение Определение пирамиды Площадь пирамиды Правильная
- 4. ОпределениеПирамида – многогранник, составленный из n -
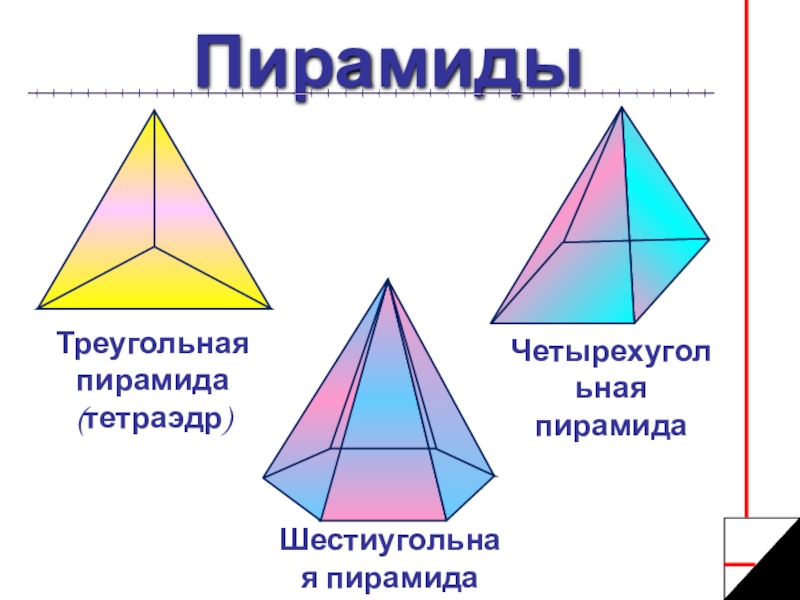
- 5. ПирамидыТреугольная пирамида (тетраэдр)Шестиугольная пирамидаЧетырехугольная пирамида
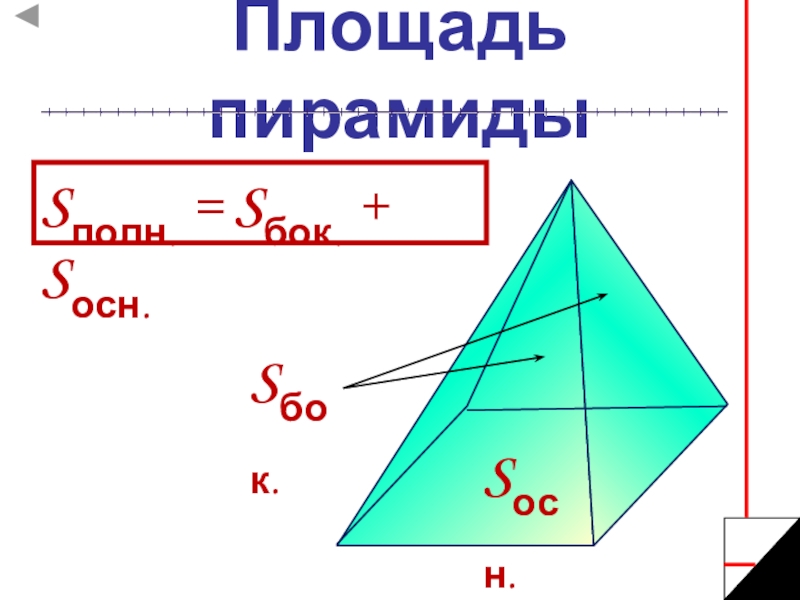
- 6. Площадь пирамидыSполн. = Sбок. + Sосн. Sбок.Sосн.
- 7. Правильная пирамидаПирамида называется правильной, если ее основание
- 8. Все боковые ребра правильной пирамиды равны, а
- 9. Док – во:2) т. к. РА1 =
- 10. Апофема – высота боковой грани правильной пирамиды,
- 11. Теорема о площади боковой поверхности правильной
- 12. Усеченная пирамидамногогранник, образованный пирамидой и её сечением,
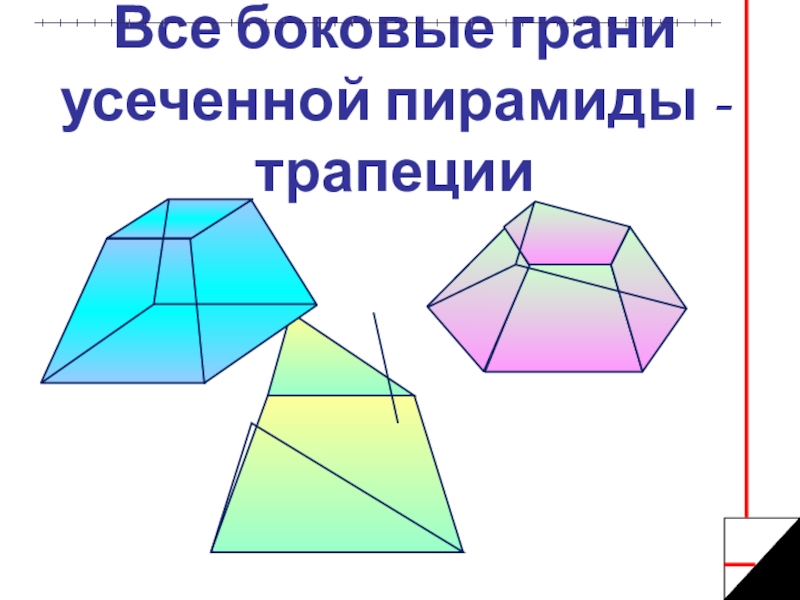
- 13. Все боковые грани усеченной пирамиды - трапеции
- 14. Усеченная пирамида называется правильной, если она получена
- 15. Теорема о площади боковой поверхности правильной усеченной
- 16. Итог урока Что называется пирамидой?Правильной пирамидой?Усеченной
- 17. Презентация подготовлена по материалам сайта
Слайд 3Содержание
ОпределениеОпределение Определение пирамиды
Площадь пирамиды
Правильная пирамида
Свойство пирамиды
Теорема о площади боковой поверхности правильной пирамиды
Усеченная пирамида
Правильная усеченная пирамида
Теорема о площади боковой поверхности правильной усеченной пирамиды
Слайд 4Определение
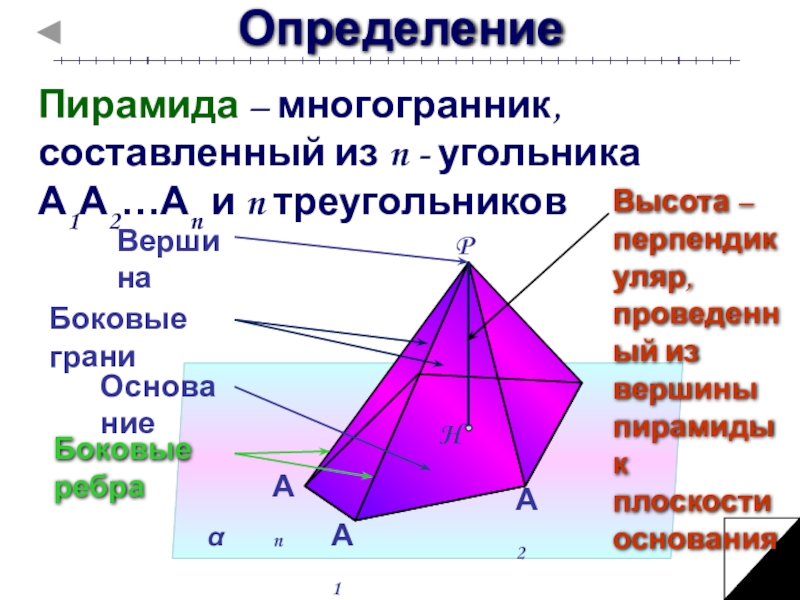
Пирамида – многогранник, составленный из n - угольника А1А2…Аn и n
Высота – перпендикуляр, проведенный из вершины пирамиды к плоскости основания
Боковые ребра
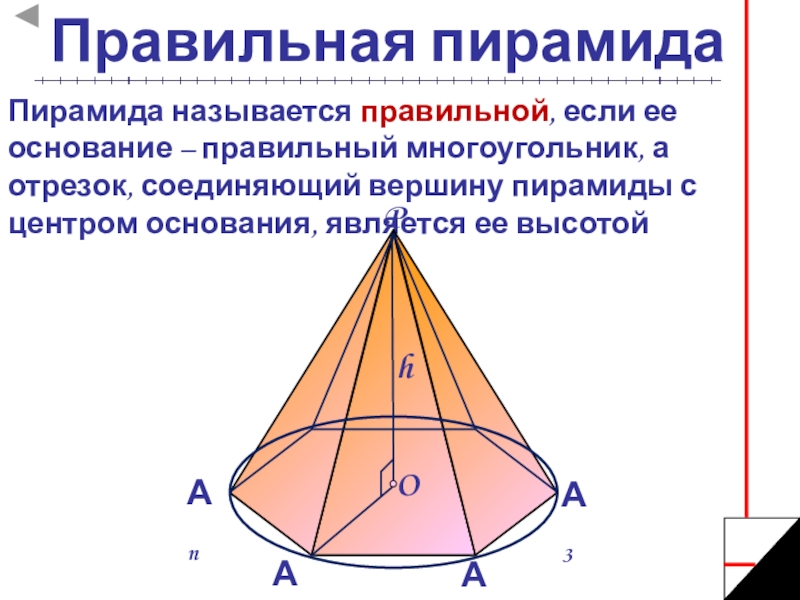
Слайд 7Правильная пирамида
Пирамида называется правильной, если ее основание – правильный многоугольник, а
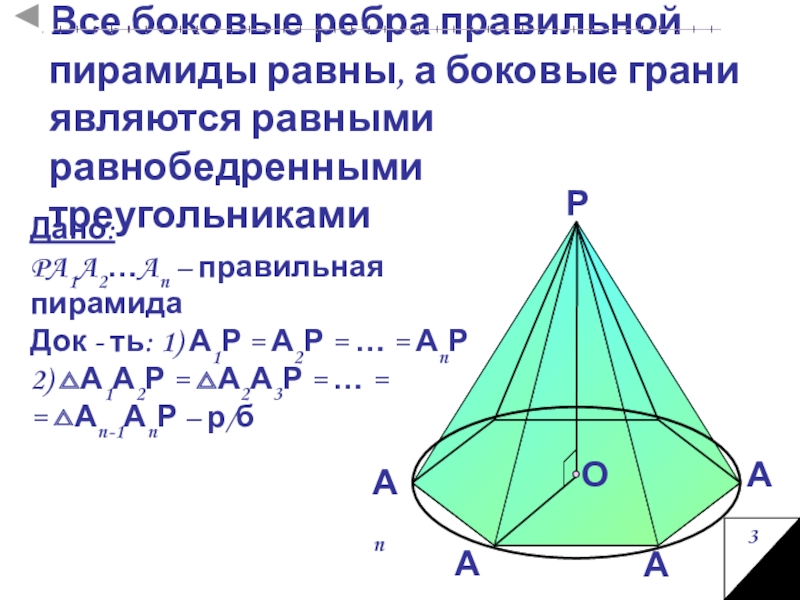
Слайд 8Все боковые ребра правильной пирамиды равны, а боковые грани являются равными
Дано:
PA1A2…An – правильная пирамида
Док - ть: 1) А1Р = А2Р = … = АnР
2) △А1А2Р = △А2А3Р = … =
= △Аn-1АnР – р/б
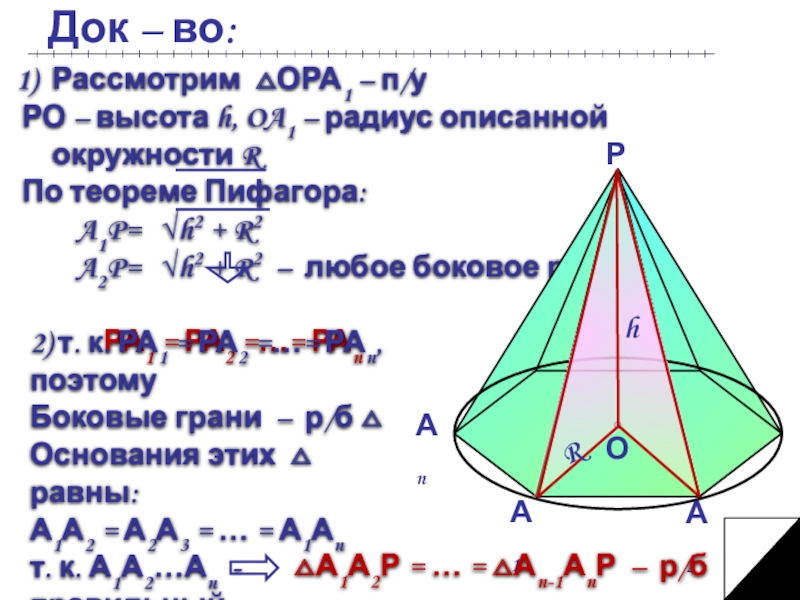
Слайд 9Док – во:
2) т. к. РА1 = РА2 =…= РАn, поэтому
Боковые грани – р/б △
Основания этих △ равны:
А1А2 = А2А3 = … = А1Аn
т. к. А1А2…Аn - правильный многоугольник
△А1А2Р = … = △Аn-1АnР – р/б
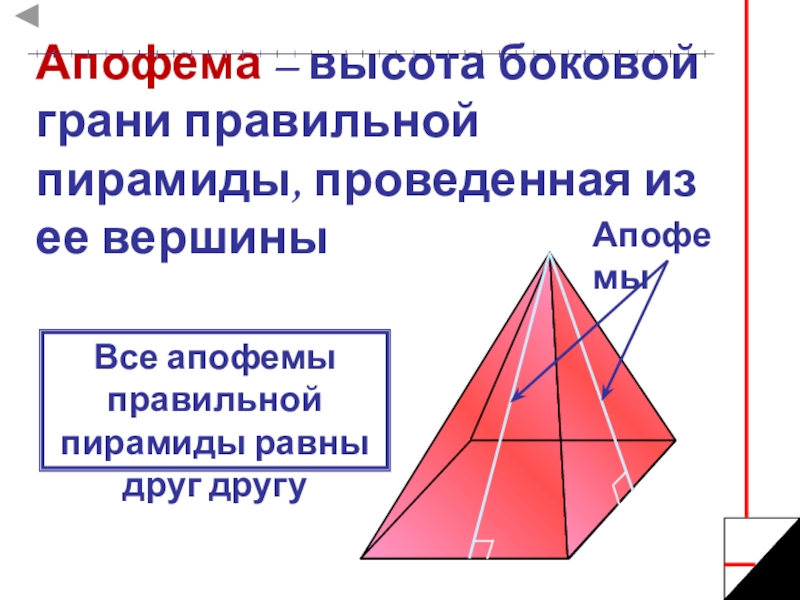
Слайд 10Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины
Апофемы
Все апофемы правильной пирамиды равны друг другу
Слайд 11Теорема о площади боковой
поверхности правильной пирамиды
Площадь боковой поверхности правильной пирамиды
Док – во:
Sбок = (½ad + ½ad + ½ad) =
= ½d(a + a + a)= ½dP
Sбок = ½dP
Слайд 12
Усеченная пирамида
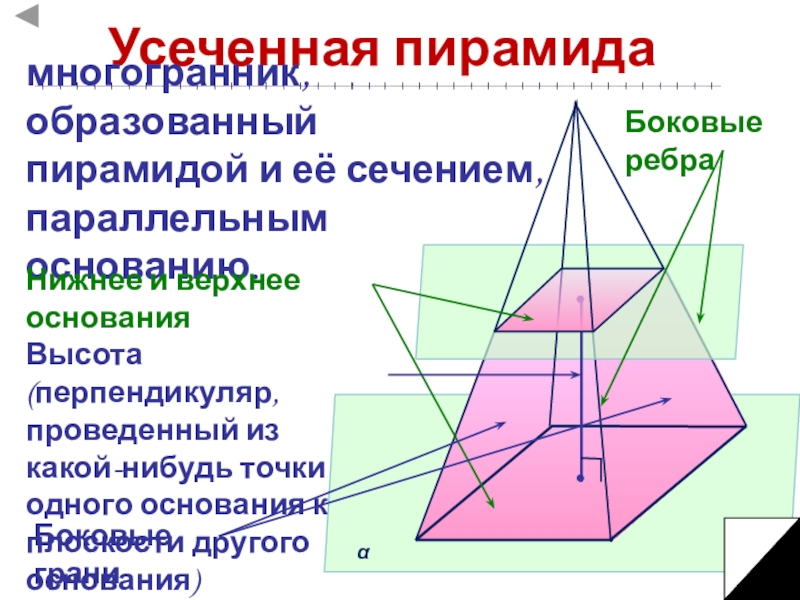
многогранник, образованный пирамидой и её сечением, параллельным основанию.
Нижнее и
Боковые грани
Боковые ребра
Высота (перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания)
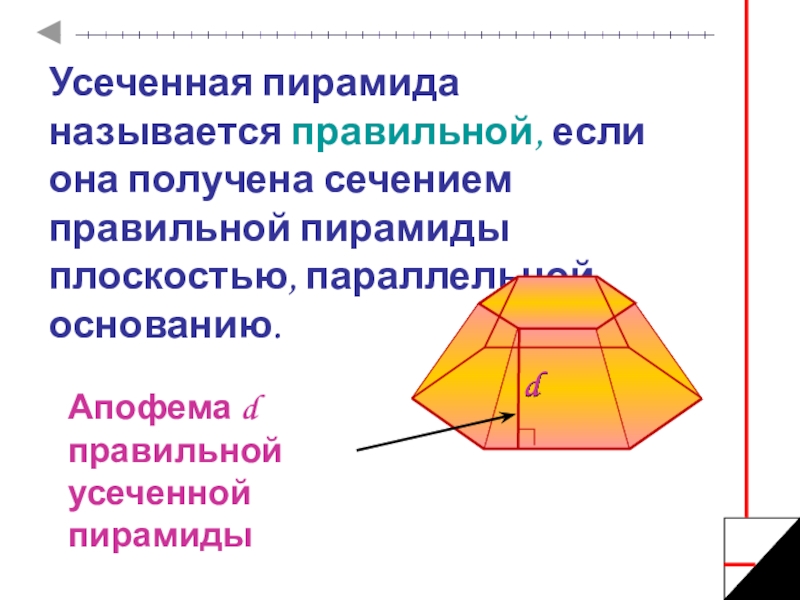
Слайд 14Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью,
Апофема d правильной усеченной пирамиды
Слайд 15Теорема о площади боковой поверхности правильной усеченной пирамиды
Площадь боковой поверхности правильной
S бок = ½(Р1 + Р2) d
P1= 4a1
P2= 4a2
Док – во:
S бок = ½d(a1+a2) + ½d(a1+a2) +
+ ½ d(a1+a2) + ½d(a1+a2) =
= ½d(a1+ a2+ a1+ a2+ a1+ a2+ a1+ a2) =
= ½d(4a1+ 4a2) = ½d(P1+ P2)
Слайд 16Итог урока
Что называется пирамидой?
Правильной пирамидой?
Усеченной пирамидой?
Что называется площадью боковой поверхности
Что называется площадью полной поверхности пирамиды?
Чему равна площадь боковой поверхности правильной пирамиды?