- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Многогранники 10 класс
Содержание
- 1. Презентация по геометрии на тему: Многогранники 10 класс
- 2. Отрезки, соединяющие вершины многогранника, не принадлежащие одной
- 3. Многогранник, поверхность которого состоит из шести квадратовМногогранник,
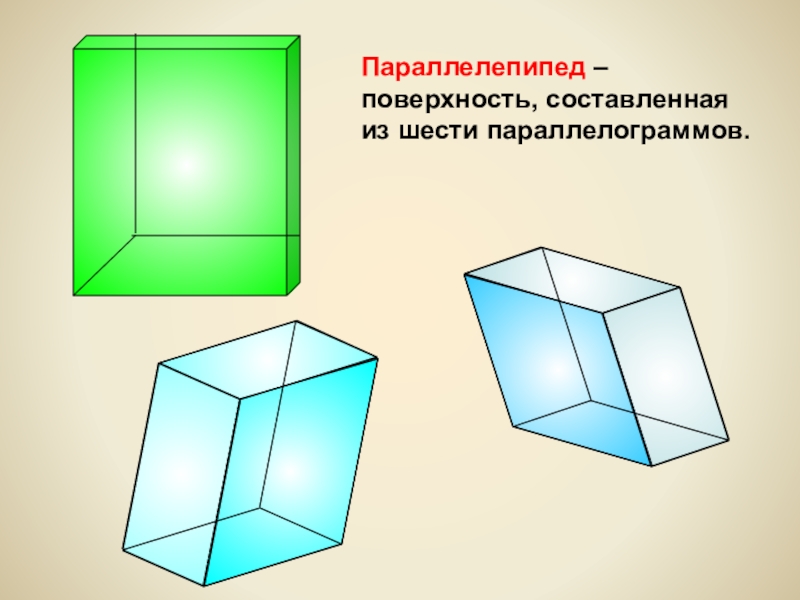
- 4. Параллелепипед – поверхность, составленная из шести параллелограммов.
- 5. Прямоугольный параллелепипедМногогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
- 6. Невыпуклый многогранник
- 7. Тетраэдр – поверхность, составленная из четырех треугольников.
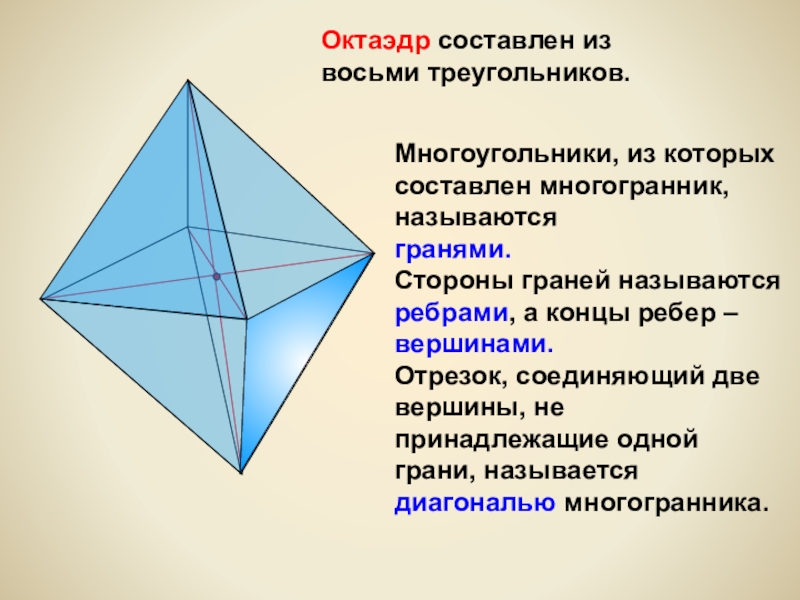
- 8. Октаэдр составлен из восьми треугольников.Многоугольники, из которых
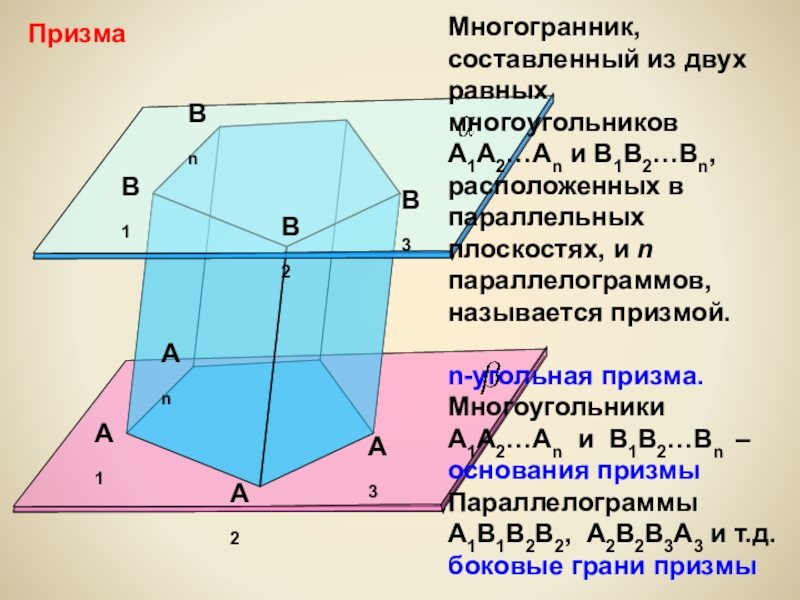
- 9. ПризмаА1А2АnB1B2BnB3А3Многогранник, составленный из двух равных многоугольников А1А2…Аn
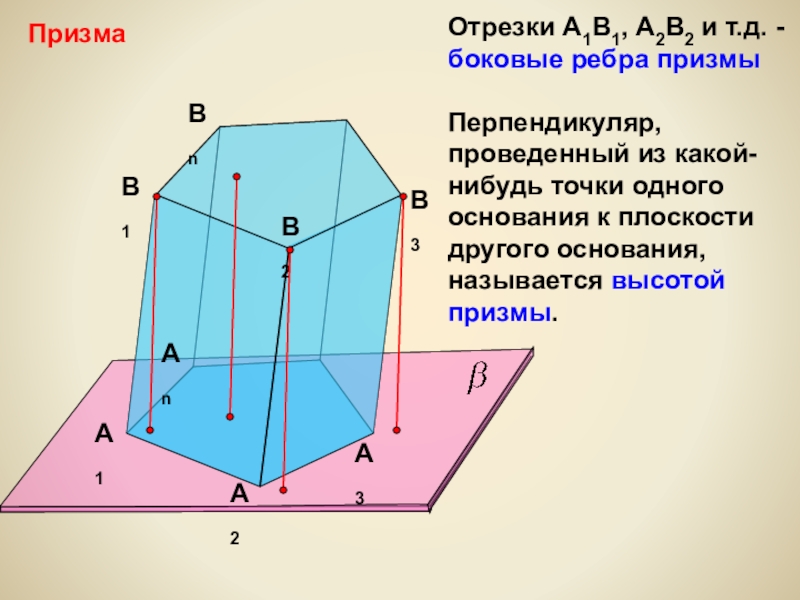
- 10. ПризмаА1А2АnB1B2BnB3А3Отрезки А1В1, А2В2 и т.д. - боковые
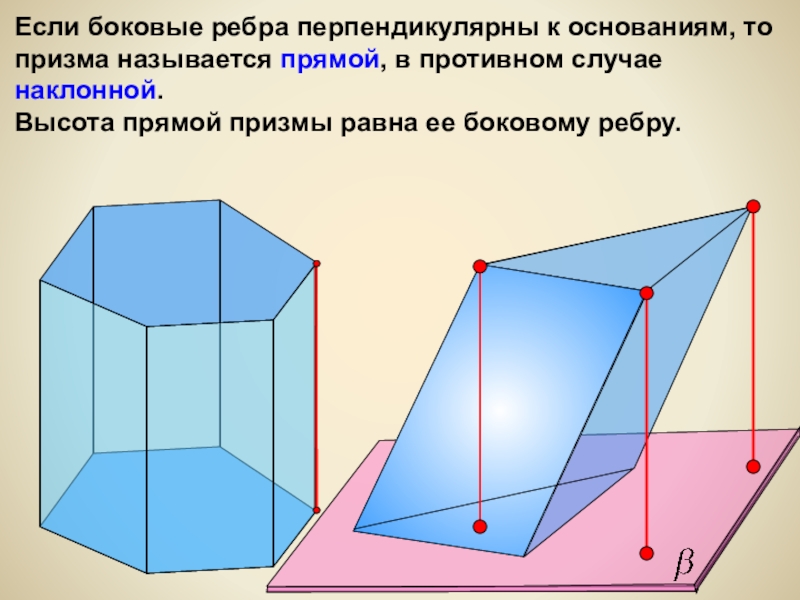
- 11. Если боковые ребра перпендикулярны к основаниям, то
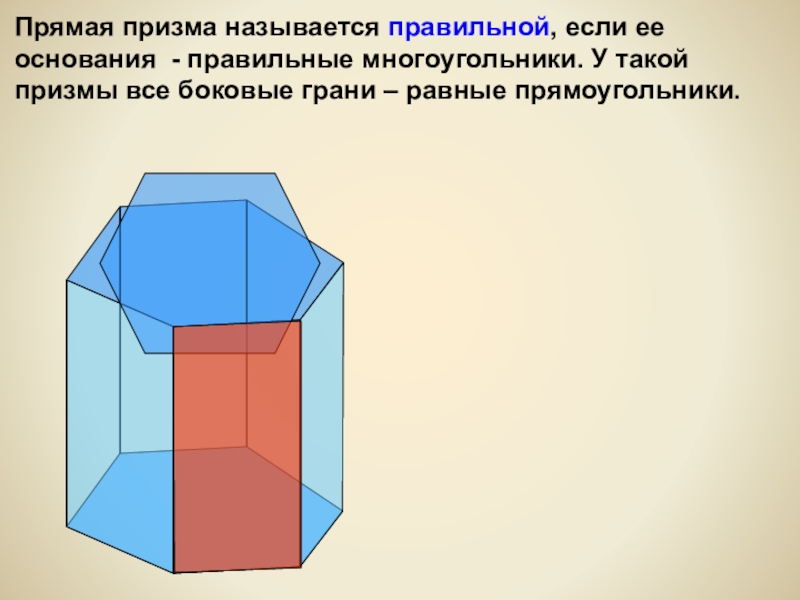
- 12. Прямая призма называется правильной, если ее основания
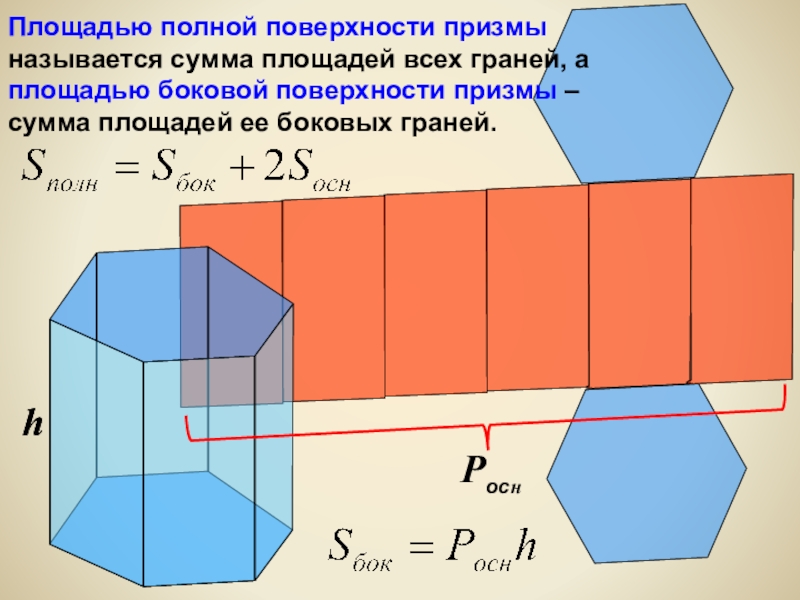
- 13. Площадью полной поверхности призмы называется сумма площадей
- 14. Основанием
- 15. Слайд 15
- 16. Сторона
- 17. Многогранник, поверхность которого состоит из двух
- 18. Площадь призмыSбок. + 2SоснSбок. = PhabhТеорема: Площадь
- 19. Многогранник, поверхность которого состоит из многоугольника и
- 20. Основание правильный многоугольник, высота опущена в центр
- 21. Усеченная пирамидаБоковые грани – трапецииТеорема: Площадь боковой
- 22. Правильные многогранники
Отрезки, соединяющие вершины многогранника, не принадлежащие одной грани, называются диагоналями.Многогранником называется тело, поверхность которого состоит из конечного числа многоугольников, называемых гранями.Стороны и вершины этих многоугольников называются ребрами и вершинами.
Слайд 2Отрезки, соединяющие вершины многогранника, не принадлежащие одной грани, называются диагоналями.
Многогранником
называется
тело,
поверхность которого
состоит из конечного
числа многоугольников,
называемых гранями.
поверхность которого
состоит из конечного
числа многоугольников,
называемых гранями.
Стороны и вершины этих многоугольников
называются ребрами и вершинами.
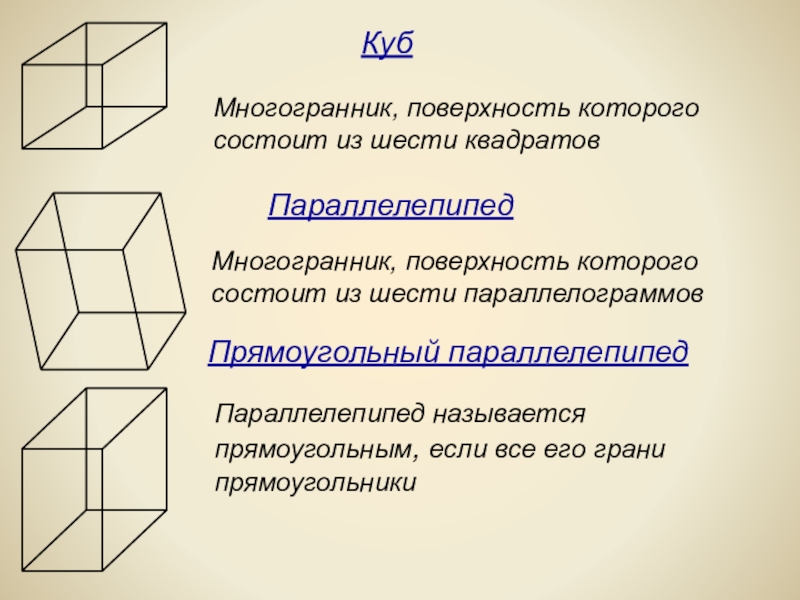
Слайд 3Многогранник, поверхность которого состоит из шести квадратов
Многогранник, поверхность которого
состоит из
шести параллелограммов
Параллелепипед называется прямоугольным, если все его грани прямоугольники
Куб
Прямоугольный параллелепипед
Параллелепипед
Слайд 5
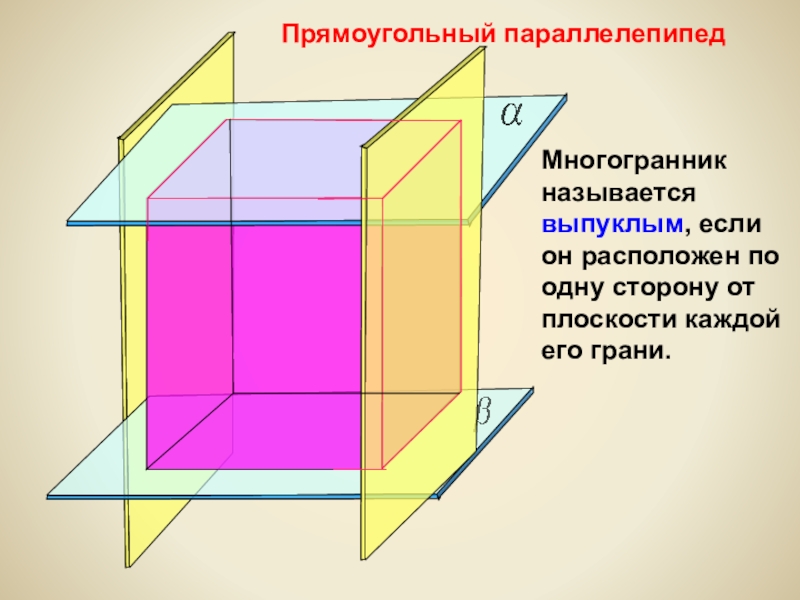
Прямоугольный параллелепипед
Многогранник называется выпуклым, если он расположен по одну сторону от
плоскости каждой его грани.
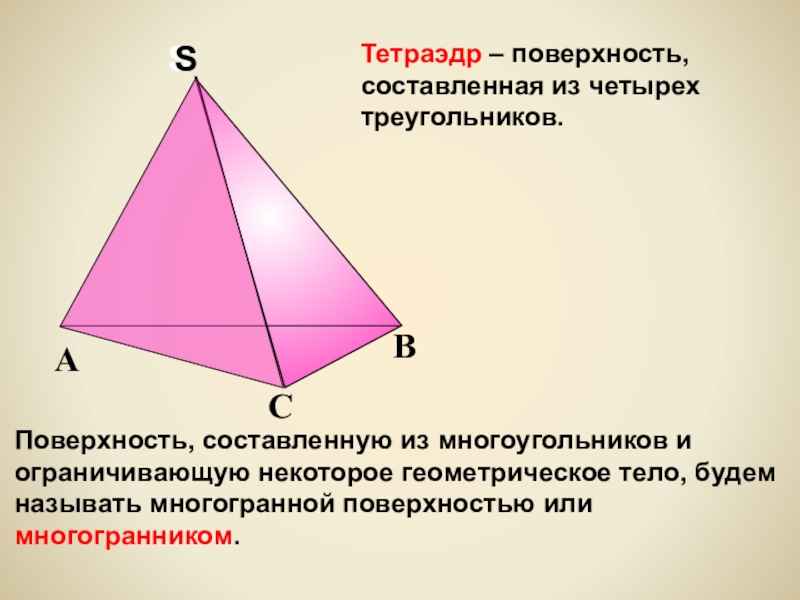
Слайд 7Тетраэдр – поверхность, составленная из четырех треугольников.
Поверхность, составленную из многоугольников
и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.
Слайд 8Октаэдр составлен из восьми треугольников.
Многоугольники, из которых составлен многогранник, называются
гранями.
Стороны
граней называются ребрами, а концы ребер – вершинами.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Слайд 9
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных в
параллельных плоскостях, и n параллелограммов, называется призмой.
n-угольная призма.
Многоугольники
А1А2…Аn и В1В2…Вn – основания призмы
Параллелограммы А1В1В2В2, А2В2В3А3 и т.д. боковые грани призмы
n-угольная призма.
Многоугольники
А1А2…Аn и В1В2…Вn – основания призмы
Параллелограммы А1В1В2В2, А2В2В3А3 и т.д. боковые грани призмы
Слайд 10
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Отрезки А1В1, А2В2 и т.д. -
боковые ребра призмы
Перпендикуляр, проведенный из
какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Слайд 11
Если боковые ребра перпендикулярны к основаниям, то призма называется прямой, в
противном случае наклонной.
Высота прямой призмы равна ее боковому ребру.
Высота прямой призмы равна ее боковому ребру.
Слайд 12
Прямая призма называется правильной, если ее основания - правильные многоугольники. У
такой призмы все боковые грани – равные прямоугольники.
Слайд 13Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью
боковой поверхности призмы – сумма площадей ее боковых граней.
h
h
Pocн
Слайд 14
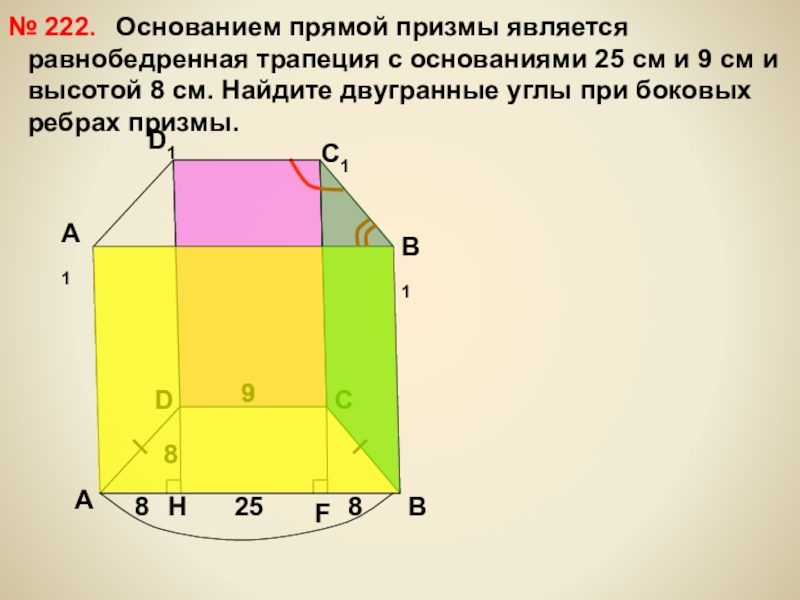
Основанием прямой призмы является равнобедренная
трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двугранные углы при боковых ребрах призмы.
№ 222.
25
9
8
H
В
С
D
А1
D1
С1
В1
А
9
Слайд 15
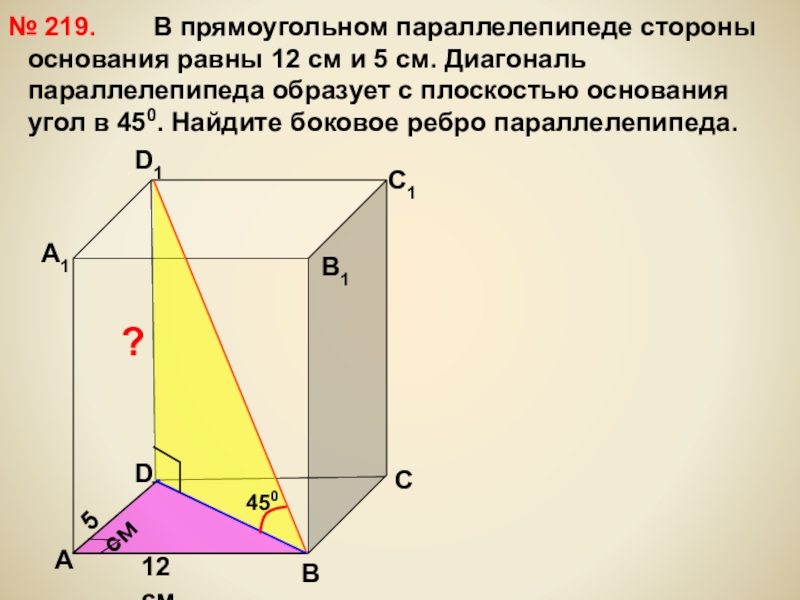
В прямоугольном
параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите боковое ребро параллелепипеда.
№ 219.
В
С
А1
D1
С1
В1
?
D
А
12 см
5 см
Слайд 16
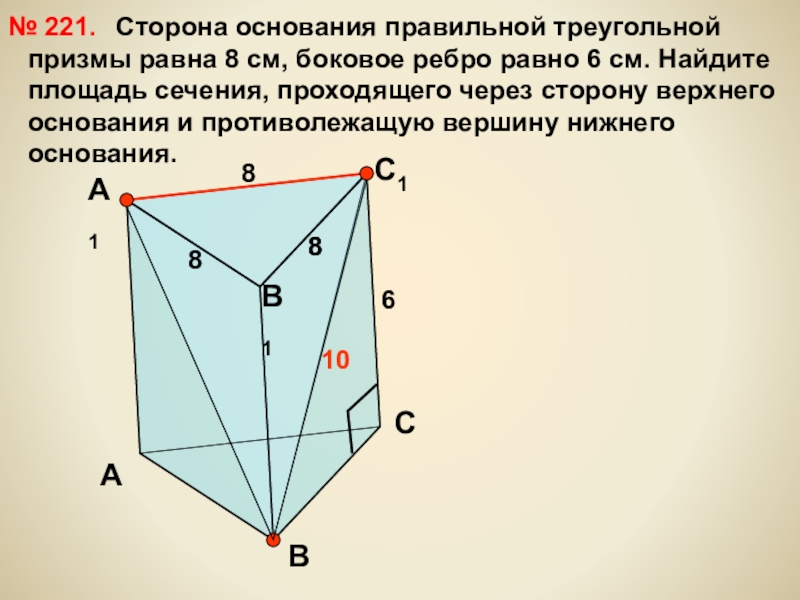
Сторона основания правильной треугольной призмы
равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
№ 221.
А
В
С
С1
В1
А1
8
6
8
8
8
10
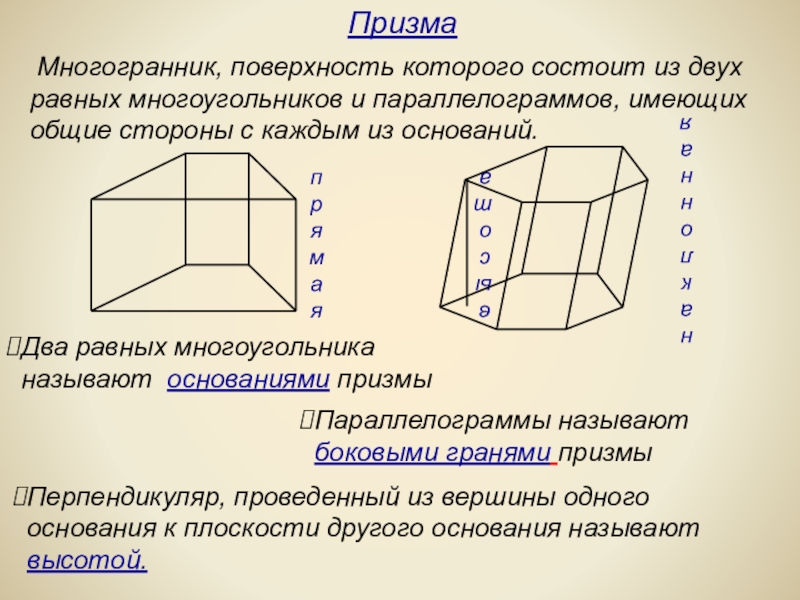
Слайд 17 Многогранник, поверхность которого состоит из двух равных многоугольников и параллелограммов,
имеющих общие стороны с каждым из оснований.
вы
с
ота
п
р
я
м
а
я
н
а
к
л
о
н
н
а
я
Призма
Два равных многоугольника называют основаниями призмы
Параллелограммы называют
боковыми гранями призмы
Перпендикуляр, проведенный из вершины одного
основания к плоскости другого основания называют
высотой.
Слайд 18Площадь призмы
Sбок. + 2Sосн
Sбок. = Ph
a
b
h
Теорема: Площадь боковой поверхности прямой
призмы
равна произведению периметра основания
на высоту.
на высоту.
Sбок. = ah + ah +bh + bh =
= h( 2a + 2b) = Ph
Sполн. =
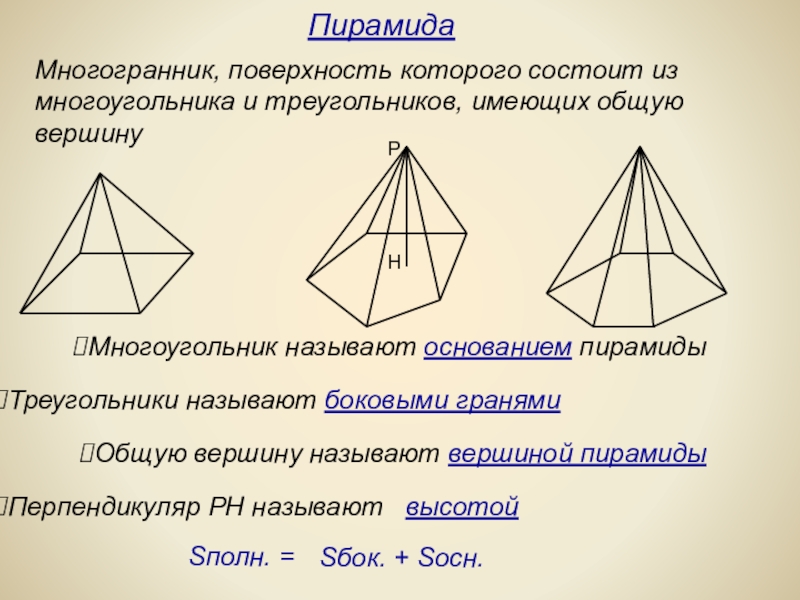
Слайд 19Многогранник, поверхность которого состоит из многоугольника и треугольников, имеющих общую вершину
Многоугольник
называют основанием пирамиды
Треугольники называют боковыми гранями
Общую вершину называют вершиной пирамиды
Перпендикуляр РН называют высотой
Sбок. + Sосн.
Н
Р
Пирамида
Sполн. =
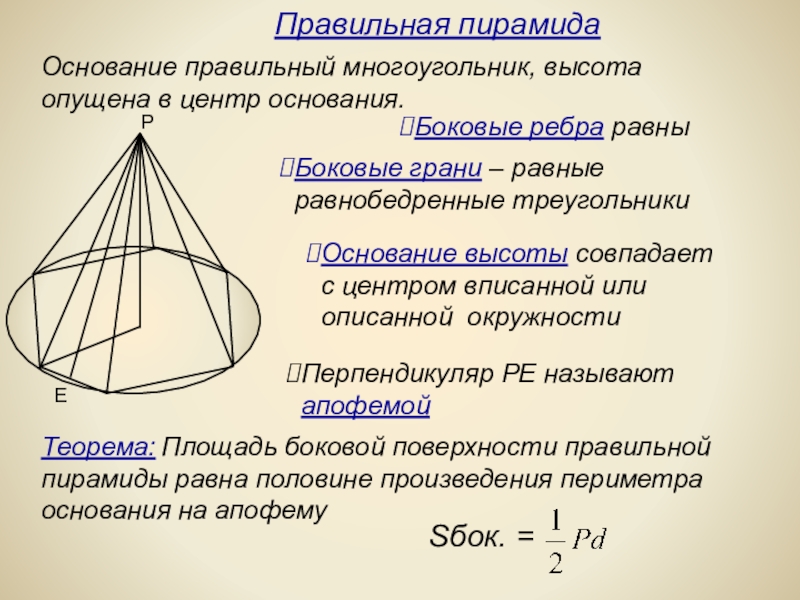
Слайд 20Основание правильный многоугольник, высота опущена в центр основания.
Перпендикуляр РЕ называют
апофемой
Теорема: Площадь боковой поверхности правильной
пирамиды равна половине произведения периметра
основания на апофему
Р
Е
Правильная пирамида
Боковые ребра равны
Боковые грани – равные равнобедренные треугольники
Основание высоты совпадает
с центром вписанной или
описанной окружности
Слайд 21Усеченная пирамида
Боковые грани – трапеции
Теорема: Площадь боковой поверхности правильной
усеченной пирамиды
равна половине произведения
полусуммы периметров оснований на апофему
полусуммы периметров оснований на апофему
