- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Геометрический гурман
Содержание
- 1. Презентация по геометрии Геометрический гурман
- 2. Геометрия – витамин для мозга.
- 3. Геометрия на плоскостиТреугольник – это должен знать
- 4. Геометрия на плоскостиТреугольник – это должен знать
- 5. Геометрия на плоскостиТреугольник – это должен знать
- 6. Треугольник – это должен знать каждый!Свойство биссектрисы
- 7. Треугольник – это должен знать каждый!2) Следствие
- 8. Четырехугольник – это должен знать каждый!Признаки и
- 9. Четырехугольник – это должен знать каждый!Прямоугольник. Прямоугольником
- 10. Четырехугольник – это должен знать каждый!Теорема о
- 11. Четырехугольник – это должен знать каждый!Теорема о
- 12. Шестиугольник – это должен знать каждый!Сумма углов
- 13. Длина дуги AB равнаШестиугольник – это должен
- 14. Окружность – это должен знать каждый!Окружность. Окружностью
- 15. Окружность – это должен знать каждый!Касательная к
- 16. Если в четырехугольник можно вписать окружность, то
- 17. Окружность – это должен знать каждый!3) Угол
- 18. Геометрия на плоскостиТреугольникЧетырехугольникШестиугольникОкружностьШесть фактов наиболее часто используемых
- 19. Геометрия на плоскостиТреугольникЧетырехугольникШестиугольникОкружностьШесть фактов наиболее часто используемых
- 20. Полезные свойства высот, медиан и биссектрисНекоторые полезные
- 21. Геометрия на плоскостиТреугольникЧетырехугольникШестиугольникОкружностьГурманоманияТеорема ЧевыТри чевианы AA',BB',CC’ треугольника ABC проходят через
- 22. Геометрия на плоскостиТреугольникЧетырехугольникШестиугольникОкружностьГурманомания Теорема Ван – Обеля
- 23. Геометрия на плоскостиТреугольникЧетырехугольникШестиугольникОкружностьГурманоманияТеорема МенелаяЕсли прямая пересекает стороны
- 24. Геометрия на плоскостиТреугольникЧетырехугольникШестиугольникОкружностьГурманоманияСимедиана – чевиана, симметричная медиане
- 25. Геометрия на плоскостиТреугольникЧетырехугольникШестиугольникОкружностьГурманоманияОсновная задача: прямая, содержащая симедиану
- 26. Геометрия на плоскостиТреугольникЧетырехугольникШестиугольникОкружностьГурманоманияВсероссийская олимпиада по геометрии 2012Дан
- 27. Геометрия на плоскостиТреугольникЧетырехугольникШестиугольникОкружностьГурманоманияТеорема. Основания перпендикуляров, опущенных на
- 28. https://foxford.ru/about_foxfordПодготовка кОГЭКарточки«Я знаю геометрию!»https://yadi.sk/i/DkmOQFo_3amodPЖелаю удачи!
Слайд 2Геометрия – витамин для мозга.
Планиметрия
Стереометрия
Аналитическая
геометрия
Начертательная
геометрия
Слайд 3Геометрия на плоскости
Треугольник – это должен знать каждый!
Признаки равенства треугольников.
1)Если
равны двум сторонам и углу между ними другого треугольника, то
треугольники равны.
2) Если сторона и два прилежащих к ней угла одного треугольника
Соответственно равны стороне и двум прилежащим к ней углам другого
треугольника, то треугольники равны.
3) Если три стороны одного треугольника соответственно равны трем сторонам
другого треугольника, то треугольники равны.
Основные свойства и признаки равнобедренного треугольника.
1) Углы при основании равнобедренного треугольника равны.
2) Медиана равнобедренного треугольника, проведенная к основанию, является
биссектрисой и высотой.
3) Если два угла треугольника равны, то он равнобедренный.
4) Если медиана треугольника является его высотой, то треугольник
равнобедренный.
5) Если биссектриса треугольника является его высотой, то треугольник
равнобедренный.
6) Если медиана треугольника является его биссектрисой, то треугольник
равнобедренный.
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 4Геометрия на плоскости
Треугольник – это должен знать каждый!
Теорема о сумме углов
1) Сумма внутренних углов треугольника равна 180◦.
2) Внешний угол треугольника равен сумме двух внутренних не смежных с
ним углов.
3) Сумма внутренних углов выпуклого n-угольника равна 180◦(n−2).
4) Сумма внешних углов n-угольника равна 360◦.
5) Углы со взаимно перпендикулярными сторонами равны, если они оба
острые или оба тупые.
Признаки равенства прямоугольных треугольников.
По двум катетам. 2) По катету и гипотенузе.
3) По гипотенузе и острому углу. 4) По катету и острому углу.
Катет прямоугольного треугольника, лежащий против угла в 30◦, равен
половине гипотенузы.
Неравенство треугольника. Сумма двух сторон треугольника
больше третьей стороны.
Средняя линия треугольника. Отрезок, соединяющий середины
двух сторон треугольника называется средней линией треугольника.
Теорема о средней линии треугольника. Средняя линия треугольника
параллельна стороне треугольника и равна ее половине.
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 5Геометрия на плоскости
Треугольник – это должен знать каждый!
Теорема о медианах треугольника.
одной точке и делятся ею в отношении 2 : 1, считая от вершины.
Медиана прямоугольного треугольника, проведенная из вершины прямого
угла, равна половине гипотенузы.
Свойство серединных перпендикуляров к сторонам треугольника.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной
точке, которая является центром окружности, описанной около треугольника.
Теорема о высотах треугольника. Прямые, содержащие высоты треугольника,
пересекаются в одной точке.
Теорема о биссектрисах треугольника. Биссектрисы треугольника
пересекаются в одной точке, которая является центром окружности,
вписанной в треугольник.
Подобие. Признаки подобия треугольников.
1) Если две стороны одного треугольника соответственно пропорциональны
двум сторонам другого, а углы, заключенные между этими сторонами, равны, то
треугольники подобны.
2) Если два угла одного треугольника соответственно равны двум углам другого,
то треугольники подобны.
3) Если три стороны одного треугольника соответственно пропорциональны
трем сторонам другого, то треугольники подобны.
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 6Треугольник – это должен знать каждый!
Свойство биссектрисы треугольника. Биссектриса треугольника делит
сторону на отрезки, пропорциональные двум другим сторонам.
Произведение основания на высоту для данного треугольника постоянно.
Тригонометрические соотношения в прямоугольном треугольнике.
1) Катет прямоугольного треугольника равен произведению гипотенузы на синус
противолежащего или на косинус прилежащего к этому катету острого угла.
2) Катет прямоугольного треугольника равен другому катету, умноженному на
тангенс противолежащего или котангенс прилежащего к этому катету острого угла.
Теорема Пифагора. Квадрат гипотенузы прямоугольного треугольника равен
сумме квадратов катетов.
Теорема, обратная теореме Пифагора. Если квадрат стороны треугольника
равен сумме квадратов двух других его сторон, то треугольник — прямоугольный.
Средние пропорциональные в прямоугольном треугольнике. Высота
прямоугольного треугольника, проведенная из вершины прямого угла, есть
среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть
Среднее пропорциональное гипотенузы и своей проекции на гипотенузу.
Метрические соотношения в треугольнике.
1)Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух
других сторон без удвоенного произведения этих сторон на косинус угла между
ними.
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 7Треугольник – это должен знать каждый!
2) Следствие из теоремы косинусов. Сумма
Параллелограмма равна сумме квадратов всех его сторон.
3) Формула для медианы треугольника. Если m — медиана треугольника,
проведенная к стороне c, то m= где a и b —остальные стороны
треугольника.
4) Теорема синусов. Стороны треугольника пропорциональны синусам
противолежащих углов.
5) Обобщенная теорема синусов. Отношение стороны треугольника к синусу
противолежащего угла равно диаметру окружности, описанной около треугольника.
Элементы равностороннего треугольника со стороной a. Пусть h,
S, r, R — высота, площадь, радиусы описанной и вписанной окружности
равностороннего треугольника со стороной a. Тогда
Формулы площади треугольника.
1) Площадь треугольника равна половине произведения основания на высоту.
2) Площадь треугольника равна половине произведения двух его сторон на синус
угла между ними.
3) Площадь треугольника равна произведению его полупериметра на радиус
вписанной окружности.
4) Площадь треугольника равна произведению трех его сторон, деленному на
учетверенный радиус описанной окружности. 5) Формула Герона.
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 8Четырехугольник – это должен знать каждый!
Признаки и свойства параллельных прямых.
1)Аксиома параллельных.
прямой, параллельной данной.
2) Если при пересечении двух прямых третьей образуются равные внутренние
накрест лежащие углы, то прямые параллельны.
3) Если две прямые параллельны одной и той же прямой, то они параллельны между
собой.
4) Две прямые, перпендикулярные одной и той же прямой, параллельны.
Параллелограмм. Параллелограммом называется четырехугольник,
противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма.
1) Диагональ разбивает параллелограмм на два равных треугольника.
2) Противоположные стороны параллелограмма попарно равны.
3) Противоположные углы параллелограмма попарно равны.
4) Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
5) Если противоположные стороны четырехугольника попарно равны, то этот
четырехугольник — параллелограмм.
6) Если две противоположные стороны четырехугольника равны и параллельны, то
этот четырехугольник — параллелограмм.
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 9Четырехугольник – это должен знать каждый!
Прямоугольник. Прямоугольником называется параллелограмм с прямым
Свойства и признаки прямоугольника.
1) Диагонали прямоугольника равны.
2) Если диагонали параллелограмма равны, то этот параллелограмм —
прямоугольник.
Ромб. Ромбом называется четырехугольник, все стороны которого равны.
Свойства и признаки ромба.
1) Диагонали ромба перпендикулярны.
2) Диагонали ромба делят его углы пополам.
3) Если диагонали параллелограмма перпендикулярны, то этот параллелограмм —
ромб.
4) Если диагонали параллелограмма делят его углы пополам, то этот
параллелограмм — ромб.
Квадрат. Квадратом называется прямоугольник, все стороны которого равны.
Свойство середин сторон четырехугольника. Середины сторон любого
четырехугольника являются вершинами параллелограмма.
Трапеция. Трапецией называется четырехугольник, у которого только две
противоположные стороны (основания) параллельны. Средней линией трапеции
называется отрезок, соединяющий середины непараллельных сторон
(боковых сторон)
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 10Четырехугольник – это должен знать каждый!
Теорема о средней линии трапеции. Средняя
основаниям и равна их полусумме.
Отрезок, соединяющий середины диагоналей трапеции, равен полуразности
оснований.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Свойства и признаки равнобедренной трапеции.
1) Углы при основании равнобедренной трапеции равны.
2) Диагонали равнобедренной трапеции равны.
3) Если углы при основании трапеции равны, то она равнобедренная.
4) Если диагонали трапеции равны, то она равнобедренная.
5) Проекция боковой стороны равнобедренной трапеции на основание равна
полуразности оснований, а проекция диагонали — полусумме оснований.
Если четырехугольник можно вписать в окружность, то сумма его
противоположных углов равна 180.
Если сумма противоположных углов четырехугольника равна180, то около
него можно описать окружность.
Если в трапецию можно вписать окружность, то боковая сторона трапеции
видна из центра окружности под прямым углом.
Если M — точка на отрезке AB, причем AM : BM =a : b, то
AM : AB =a : (a+b), BM : AB =b : (a+b).
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 11Четырехугольник – это должен знать каждый!
Теорема о пропорциональных отрезках. Параллельные прямые,
пересекающие
Замечательное свойство трапеции.
Точка пересечения диагоналей трапеции, точка пересечения продолжений
боковых сторон и середины оснований лежат на одной прямой.
Формулы площади параллелограмма.
1) Площадь параллелограмма равна произведению основания на высоту.
2) Площадь параллелограмма равна произведению его соседних сторон на синус
угла между ними.
3) Площадь прямоугольника равна произведению двух его соседних сторон.
4) Площадь ромба равна половине произведения его диагоналей.
Площадь трапеции равна произведению полусуммы оснований на высоту.
Площадь четырехугольника равна половине произведения его диагоналей на
синус угла между ними.
Если в многоугольник можно вписать окружность, то его площадь равна
произведению полупериметра многоугольника на радиус этой окружности.
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 12Шестиугольник – это должен знать каждый!
Сумма углов выпуклого шестиугольника определяется по общей
180°(n-2) и равна 720°
Правильный шестиугольник - это шестиугольник, все стороны которого равны
между собой.
Свойства правильного шестиугольника
все внутренние углы равны между собой
каждый внутренний угол правильного шестиугольника равен 120 градусам
все стороны равны между собой
сторона правильного шестиугольника равна радиусу описанной окружности
правильный шестиугольник заполняет плоскость без пробелов и наложений
Радиус описанной окружности правильного шестиугольника равен его стороне
Все внутренние углы равны 120 градусам
Радиус вписанной окружности r равен корню из трех, деленному на два и
умноженному на длину стороны
Периметр правильного шестиугольника P равен шести радиусам описанной
окружности или четыре корня из трех, умноженным на радиус вписанной
окружности
Площадь правильного шестиугольника равна трем корням из трех пополам,
умноженным на квадрат радиуса описанной окружности или квадрат стороны
либо площадь правильного шестиугольника равна двум корням из трех,
умноженным на квадрат радиуса вписанной окружности
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 13 Длина дуги AB равна
Шестиугольник – это должен знать каждый!
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
R=a
P=6a
D=2R=2a
A
C
B
D
E
F
Длина
Формула площади сектора
.
Слайд 14Окружность – это должен знать каждый!
Окружность. Окружностью называется геометрическое место точек
удаленных от данной точки, называемой центром окружности, на одно и то же
положительное расстояние.
Свойства окружности.
1) Диаметр, перпендикулярный хорде, делит ее пополам.
2) Диаметр, проходящий через середину хорды, не являющейся диаметром,
перпендикулярен этой хорде.
3) Серединный перпендикуляр к хорде проходит через центр окружности.
4) Равные хорды удалены от центра окружности на равные расстояния.
5) Хорды окружности, удаленные от центра на равные расстояния, равны.
6) Окружность симметрична относительно любого своего диаметра.
7) Дуги окружности, заключенные между параллельными хордами, равны.
8) Из двух хорд больше та, которая менее удалена от центра.
9) Диаметр есть наибольшая хорда окружности.
Замечательное свойство окружности. Геометрическое место точек M, из которых
отрезок AB виден под прямым углом (\AMB ==90), есть окружность с диаметром
AB без точек A и B.
Геометрическое место точек M, из которых отрезок AB виден под острым углом
(\AMB <90) есть внешность круга с диаметром AB без точек прямой AB.
Геометрическое место точек M, из которых отрезок AB виден под тупым углом
(\AMB >90), есть внутренность круга с диаметром АB без точек отрезка AB.
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 15Окружность – это должен знать каждый!
Касательная к окружности. Прямая, имеющая с
общую точку, называется касательной к окружности.
1) Касательная перпендикулярна радиусу, проведенному в точку касания.
2) Если прямая l, проходящая через точку на окружности, перпендикулярна
радиусу, проведенному в эту точку, то прямая l — касательная к окружности.
3) Если прямые, проходящие через точку M, касаются окружности в точках A и B,
то MA=MB.
4) Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Радиус окружности, вписанной в прямоугольный треугольник с катетами a, b
и гипотенузой c, равен (a+b −c)/2
Если M — точка касания со стороной AC окружности, вписанной в
треугольник ABC, то AM = p −BC, где p — полупериметр треугольника.
Окружность касается стороны BC треугольника ABC и продолжений сторон
AB и AC. Тогда расстояние от вершины A до точки касания окружности с
прямой AB равно полупериметру треугольника ABC.
Окружность, вписанная в треугольник ABC, касается сторон AB, BC и AC
в точках K, L и M. Если \BAC = а, то \KLM =90 −а/2.
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 16Если в четырехугольник можно вписать окружность, то суммы
его противоположных сторон равны.
Окружность
Если в четырехугольник можно вписать окружность, то суммы его
противоположных сторон равны.
Касающиеся окружности.
Говорят, что две окружности касаются, если они имеют единственную общую
точку (точка касания).
1) Точка касания двух окружностей лежит на их линии центров.
2) Окружности радиусов r и R с центрами O1 и O2 касаются внешним образом
тогда и только тогда, когда R +r =O1O2.
3) Окружности радиусов r и R (r < R) с центрами O1 и O2 касаются внутренним
образом тогда и только тогда, когда R −r =O1O2.
4) Окружности с центрами O1 и O2 касаются внешним образом в точке K.
Некоторая прямая касается этих окружностей в различных точках A и B и
пересекается с общей касательной, проходящей через точку K, в точке C.
Тогда угол AKB =90 и угол O1CO2 =90.
Углы, связанные с окружностью.
1) Угловая величина дуги окружности равна угловой величине центрального угла.
2) Вписанный угол равен половине угловой величины дуги, на которую он
опирается.
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 17Окружность – это должен знать каждый!
3) Угол между пересекающимися хордами равен
высекаемых хордами.
4) Угол между двумя секущими равен полуразности дуг, высекаемых секущими на
окружности.
5) Угол между касательной и хордой равен половине угловой величины дуги,
заключенной между ними.
Площадь круга радиуса R
Длина окружности радиуса R
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 18Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
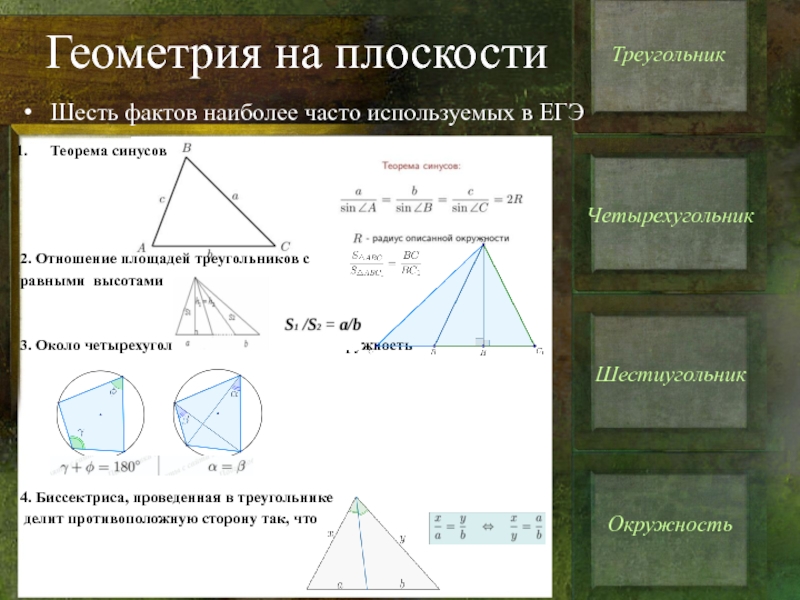
Шесть фактов наиболее часто используемых в ЕГЭ
Теорема синусов
2.
равными высотами
3. Около четырехугольника можно описать окружность
4. Биссектриса, проведенная в треугольнике
делит противоположную сторону так, что
Слайд 19Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Шесть фактов наиболее часто используемых в ЕГЭ
5. Дуги, заключенные
тогда АВСD – равнобедренная трапеция.
6. Медиана, проведенная из прямого угла, равна
половине гипотенузы.
Некоторые полезные свойства биссектрисы
Если биссектрисы углов B и C треугольника ABC пересекаются
в точке M, то \BMC =90 +\A/2.
Угол между биссектрисами смежных углов равен 90.
Биссектрисы внутренних односторонних углов при параллельных
прямых и секущей перпендикулярны.
Биссектрисы углов при боковой стороне трапеции пересекаются на ее
средней линии.
Теорема Штейнера—Лемуса. Если две биссектрисы треугольника
равны, то он равнобедренный
Слайд 20Полезные свойства высот, медиан и биссектрис
Некоторые полезные свойство высот
Высоты параллелограмма, опущенные из
вершины, образуют угол, равный углу
параллелограмма при соседней вершине
В трапеции с перпендикулярными
диагоналями ее высота равна средней линии
FH=(BC+AD)/2
Некоторые полезные свойство медиан
В равнобедренном треугольнике две медианы,
проведенные к равным сторонам треугольника, равны, а третья медиана
одновременно является биссектрисой и высотой.
Если в треугольнике две медианы равны, то треугольник —
равнобедренный, а третья медиана одновременно является биссектрисой
и высотой угла при своей вершине.
Медиана разбивает треугольник на два равновеликих треугольника.
Треугольник делится тремя медианами на шесть равновеликих
треугольников.
Если треугольник разносторонний , то его биссектриса, проведённая из
любой вершины, лежит между медианой и высотой, проведёнными из той
же вершины.
Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Слайд 21Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Гурманомания
Теорема Чевы
Три чевианы AA',BB',CC’ треугольника ABC проходят через одну точку
тогда и
|BA1|· |CB1| · |AC1|=|CA1| · |AB1| · |BC1|
= 1
Дано:
АС1:С1В=2:1
ВА1=А1С
Найти: СВ1:В1А
Решение:
=1 2 · 1 =1 = 0, 5
СВ1:В1А = 1 : 2
Ответ: СВ1:В1А = 1 : 2
2x
x
y
y
Слайд 22Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Гурманомания
Теорема Ван – Обеля
Для трех чевиан, пересекающихся
справедливо равенство:
Дано:
АА1, ВВ1, СС1 - биссектрисы
АВ + ВС = 13
АС = 8
Найти: ВО: ОВ1
Решение:
- согласно свойству биссектрис
по теореме Ван – Обеля + +
тогда т.е. ВО : ОВ1 = 13 : 8
Ответ : 13 : 8
Слайд 23Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Гурманомания
Теорема Менелая
Если прямая пересекает стороны AB и BC в
соответственно, а также продолжение прямой AC в точке B1, то
выполнено следующее соотношение:
Дано:
АВС
АС = 4
ВМ и АN – медианы, К АВ
ОК АС = Р
Найти: АР
Выделим АВМ
Т.к ВМ – медиана ВО : ОМ = 2 : 1
АМ = 2 , пусть АР – у
Ответ: АР = 4
А
В
С
Р
М
N
О
x
3x
K
Слайд 24Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Гурманомания
Симедиана – чевиана, симметричная медиане относительно
биссектрисы, проведенной из
Симедиана – чевиана, делящая противоположную сторону в
отношении квадратов прилежащих сторон.
Лемма: В треугольнике проведен отрезок,
антипараллельный одной из сторон.
Тогда прямые, содержащие медиану
большого и симедиану маленького
треугольника, совпадают.
А
В
С
М
N
А
С
В
P
K
антипараллельны
М
Слайд 25Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Гурманомания
Основная задача: прямая, содержащая симедиану треугольника проходит через точку
Задача:
В остроугольном треугольнике
ABC точки Е и F основания
Проекции высоты ВК на стороны АВ и ВС соответственно.
К окружности вокруг треугольника BEF в точках E и F проведены касательные. Требуется доказать, что их точка
пересечения лежит на прямой, содержащей медиану
треугольника .
Решение: заметим, что ВР
симедиана треугольника BEF, а
следовательно АС антипараллельна EF.
Таким образом ВМ медиана треугольника АВС.
Слайд 26Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Гурманомания
Всероссийская олимпиада по геометрии 2012
Дан АВС. Касательная в точке
прямую АВ в точке D. Касательные к описанной окружности АСD в
точках А и С пересекаются в точке К. Докажите, что прямая DK делит
отрезок ВС пополам.
Разберем решение на доске
Гармонический четырехугольник.
Определение: Вписанный в окружность четырехугольник называется
гармоническим, если произведения его противоположных сторон равны.
Свойство: диагонали гармонического четырехугольника
являются симедианами.
Лемма: если во вписанном четырехугольнике одна диагональ является симедианой,
то он гармонический.
https://yadi.sk/i/-7sPFyNP3amjvP
Слайд 27Геометрия на плоскости
Треугольник
Четырехугольник
Шестиугольник
Окружность
Гурманомания
Теорема. Основания перпендикуляров, опущенных на стороны треугольника (или их
Всероссийская олимпиада по геометрии, 2014
Дан прямоугольник ABCD. Через точку B провели две перпендикулярные прямые.
Первая прямая пересекает сторону AD в точке K, а вторая продолжение стороны CD в точке L. Пусть F – точка пересечения KL и AC. Докажите, что BF KL.
Разберем решение на доске
https://yadi.sk/i/ZmFFbnuA3ammth