- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Фигуры постоянной ширины(9 класс)
Содержание
- 1. Презентация по геометрии Фигуры постоянной ширины(9 класс)
- 2. Аннотация Крышки люков, спасающие пешеходов от падений
- 3. Тема исследованияФигуры постоянной ширины. Треугольник Рёло.Проблемный вопрос:Почему
- 4. Цель исследования1.Выяснить, что представляют собой фигуры постоянной
- 5. Методы исследованияИзучение литературы по теме.Ожидаемый результатСамостоятельное изготовление фигур постоянной ширины
- 6. Содержание проектаЦели, задачи, методы исследования. История вопроса.Определения
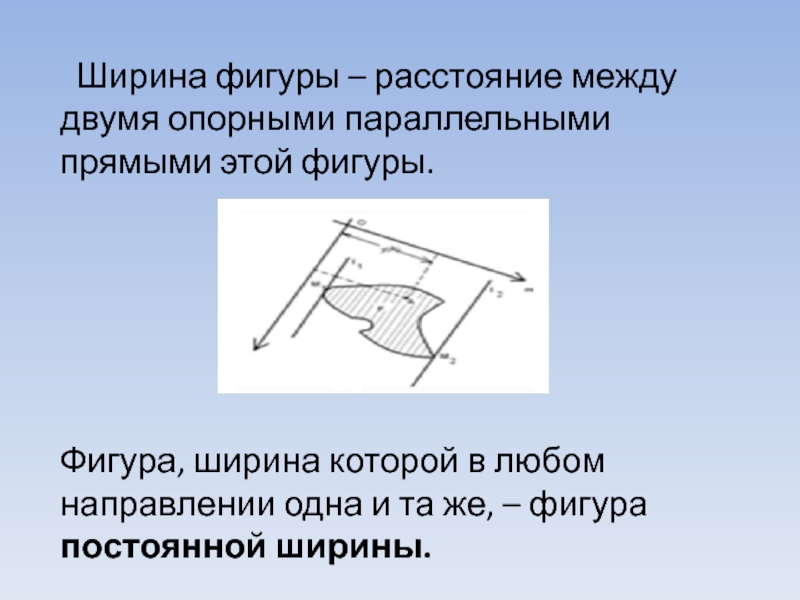
- 7. Ширина фигуры – расстояние между двумя
- 8. Круг – самая известная фигура постоянной ширины.
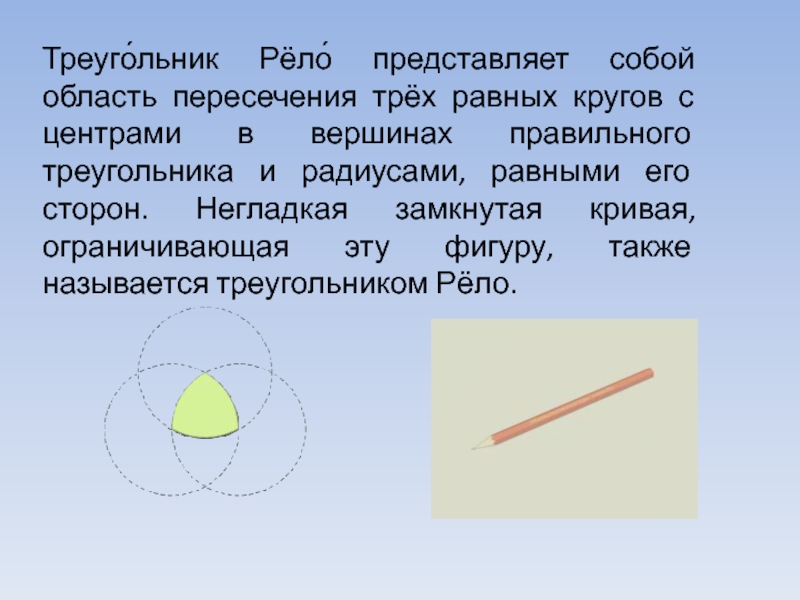
- 9. Треуго́льник Рёло́ представляет собой область пересечения трёх
- 10. Название фигуры происходит от фамилии немецкого механика
- 11. Некоторые математики считают, что первым продемонстрировал идею
- 12. Подобная фигура встречается и раньше, в XV
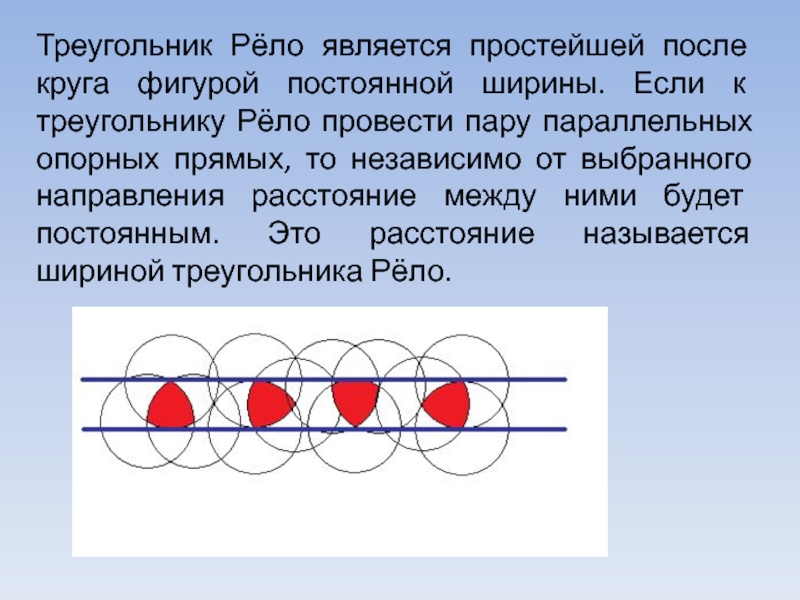
- 13. Треугольник Рёло является простейшей после круга фигурой
- 14. В житейском смысле постоянная ширина кривой означает,
- 15. Свойства треугольника Рёло (среди фигур постоянной ширины)
- 16. Благодаря своим геометрическим свойствам, фигуры постоянной ширины
- 17. Простейшая фигура постоянной ширины, как
- 18. Полдинара ( Иордания)
- 19. немецкий инженер Ф. ВанкельДвигатель Ванкеля(1957) Ротор этого
- 20. Такой трёхгранный ротор обкатывается вокруг шестерни, всё
- 21. Двигатель Ванкеля позволяет осуществить любой четырёхтактный термодинамический
- 22. В 1914 году английский инженер Гарри Джеймс
- 23. Сверло с сечением в виде треугольника Рёло
- 24. Грейферный механизм в кинопроекторах. Он основан
- 25. Форма треугольника Рёло используется и в архитектуре.
- 26. Треугольник Рёло используют и в архитектуре, не
- 27. Заключение: Колесо, изобретенное несколько тысяч лет назад, произвело
- 28. ЛитератураСайт в Интернете:ru.wikipedia.orgСайт в Интернете:etudes.ru «Этюды›Треугольник Рело
Слайд 1Фигуры
постоянной ширины.
Треугольник Рёло.
Выполнил: Миколайчук Егор
Руководитель: Назарова Г.А.
ГБОУ Гимназия №1797 «Богородская»
Слайд 2Аннотация
Крышки люков, спасающие пешеходов от падений в колодцы и мешающие
А есть ли на плоскости, помимо круга, другие фигуры постоянной ширины? Оказывается, есть, и их бесконечно много.
Самая простая и самая знаменитая фигура – треугольник Рёло. Точнее говоря, эта фигура только напоминает треугольник.
Данная работа посвящена изучению фигур постоянной ширины и в частности, треугольника Рёло, систематизации знаний о них. Она может быть полезна тем, кто увлекается геометрией.
Слайд 3Тема исследования
Фигуры постоянной ширины. Треугольник Рёло.
Проблемный вопрос:
Почему крышки люков, спасающие пешеходов
Слайд 4Цель исследования
1.Выяснить, что представляют собой фигуры постоянной ширины.
2. Показать роль и
3. Построить фигуры постоянной ширины.
Задачи исследования
1.Выяснить, как получаются фигуры постоянной ширины.
2. Показать роль и значение этих фигур.
3. Построить фигуры постоянной ширины.
Слайд 5Методы исследования
Изучение литературы по теме.
Ожидаемый результат
Самостоятельное изготовление фигур постоянной ширины
Слайд 6Содержание проекта
Цели, задачи, методы исследования.
История вопроса.
Определения и свойства фигур постоянной
Треугольник Рёло.
Практическое применение треугольника Рёло.
Заключение.
Литература.
Слайд 7 Ширина фигуры – расстояние между двумя опорными параллельными прямыми этой
Фигура, ширина которой в любом направлении одна и та же, – фигура постоянной ширины.
Слайд 8Круг – самая известная фигура постоянной ширины. Эта фигура обладает многими
Может показаться, что круг является единственной выпуклой фигурой, у которой ширина в любом направлении одна и та же. Однако существует множество других фигур постоянной ширины, симметричных и несимметричных, и способов их построения. Все эти фигуры имеют одинаковый периметр при одинаковом диаметре. Самую большую площадь ограничивает круг, а меньшую – треугольник Рело.
Слайд 9Треуго́льник Рёло́ представляет собой область пересечения трёх равных кругов с центрами
Слайд 10Название фигуры происходит от фамилии немецкого механика Франца Рёло. Он, вероятно,
1829-1905
Слайд 11Некоторые математики считают, что первым продемонстрировал идею треугольника из равных дуг
Слайд 12Подобная фигура встречается и раньше, в XV веке: её использовал в
Слайд 13Треугольник Рёло является простейшей после круга фигурой постоянной ширины. Если к
Слайд 14В житейском смысле постоянная ширина кривой означает, что если сделать катки
Слайд 15Свойства треугольника Рёло
(среди фигур постоянной ширины) :
наименьшая площадь
наименьший возможный
наименьшая симметричность относительно центра.
Треугольник получил распространение в технике — на его основе были созданы кулачковые и грейферные механизмы, роторно-поршневой двигатель Ванкеля и даже дрели, позволяющие сверлить квадратные отверстия.
Слайд 16Благодаря своим геометрическим свойствам, фигуры постоянной ширины находят применение в различных
Пример:
Вы опускаете монету в автомат и она отправляется в путь к монетоприёмнику. Чтобы монета не застряла, можно, конечно, расширить трубку. А можно изготавливать монеты в виде фигур постоянной ширины, тогда монета не застрянет, даже вращаясь.
Слайд 17 Простейшая фигура постоянной ширины, как мы знаем, - круг,
20 пенсов
50 пенсов
Слайд 19немецкий инженер
Ф. Ванкель
Двигатель Ванкеля(1957)
Ротор этого двигателя выполнен в виде треугольника
Слайд 20
Такой трёхгранный ротор обкатывается вокруг шестерни, всё время касаясь вершинами внутренних
Слайд 21Двигатель Ванкеля позволяет осуществить любой четырёхтактный термодинамический цикл без применения механизма газораспределения Смесеобразование, зажигание, смазка, охлаждение и
Слайд 22В 1914 году английский инженер Гарри Джеймс Уаттс изобрёл инструмент для
Слайд 23Сверло с сечением в виде треугольника Рёло и режущими кромками, совпадающими
Для сверления он использовал направляющий шаблон с квадратной прорезью, в котором двигалось сверло, вставленное в «плавающий патрон».
Слайд 24Грейферный механизм в кинопроекторах. Он основан на треугольнике Рёло, вписанном в
Слайд 25
Форма треугольника Рёло используется и в архитектуре.
Конструкция из двух его дуг
Слайд 26Треугольник Рёло используют и в архитектуре, не принадлежащей к готическому стилю.
Слайд 27Заключение:
Колесо, изобретенное несколько тысяч лет назад, произвело переворот в жизни человека.
Систематизируя и углубляя теоретические знания, я в треугольнике Рело (самой известной после круга фигуры постоянной ширины) обозначил его сильные и слабые стороны. Изучил основные свойства фигур постоянной ширины, историю изобретения, рассмотрел области применения фигур постоянной ширины и изучил их свойства.
Рассмотрел применение треугольника Рело в некоторых механических устройствах, в автомобильных двигателях. Поиски альтернативных видов топлива для автомобилей заставил вновь обратить внимание на роторно-поршневой двигатель Ванкеля. Разработчики Mazda уверяют, что по природе своей роторно-поршневой агрегат гораздо лучше приспособлен для работы на водороде, нежели традиционные моторы. По прогнозам специалистов, уже к 2025 году более четверти мирового автопарка будет использовать в качестве топлива водород. Сколько из этого количества придется на традиционные ДВС и как будет меняться пропорция по мере удешевления себестоимости производства компонентов привода на топливных элементах? Увидим в ближайшие годы.
Отличительные свойства треугольника Рело находят множество применений. Это доказывает, что мы должны более тщательно изучить свойства фигур постоянной ширины и находить им ещё больше применений.
Слайд 28Литература
Сайт в Интернете:ru.wikipedia.org
Сайт в Интернете:etudes.ru «Этюды›Треугольник Рело
Сайт в Интернете: nsportal.ru
Коксетер, С.М., Грейтцер, С.Л., Новые встречи с геометрией. – М., Наука, 1978.-223с.
В. Г. Болтянский, И. М. Яглом. Выпуклые фигуры. М.—Л.: ГТТИ, 1951. — 343 с.
Г. Радемахер, О. Теплиц. Числа и фигуры. М.: Физматгиз, 1962. — 263 с.
С. Г. Гиндикин. Рассказы о физиках и математиках. М.: МЦНМО, 2006.