- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 7 класс
Содержание
- 1. Презентация по геометрии 7 класс
- 2. Повторение
- 3. Теорема 3.6.Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
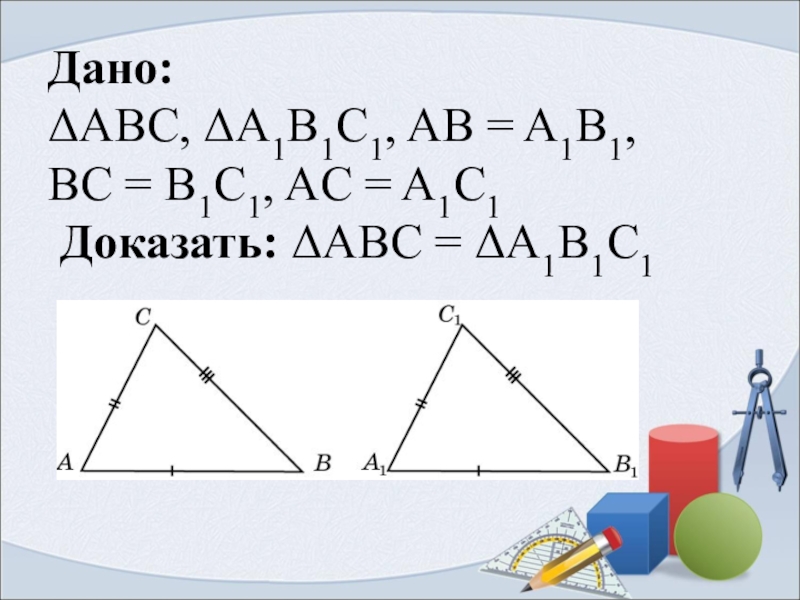
- 4. Дано: ΔABC, ΔA1B1C1, AB = A1B1, BC
- 5. Доказательство: 1) Пусть ΔABC ≠ ΔA1B1C1, тогда
- 6. Доказательство: 2) Пусть ΔABC2 = ΔA1B1C1. Пусть
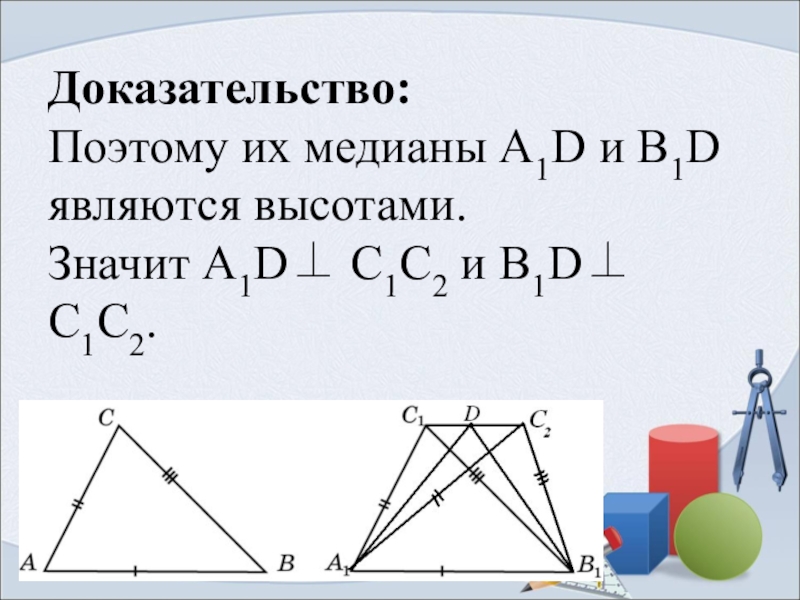
- 7. Доказательство: Поэтому их медианы А1D и В1D являются высотами. Значит А1D⊥ С1C2 и В1D⊥ С1C2.
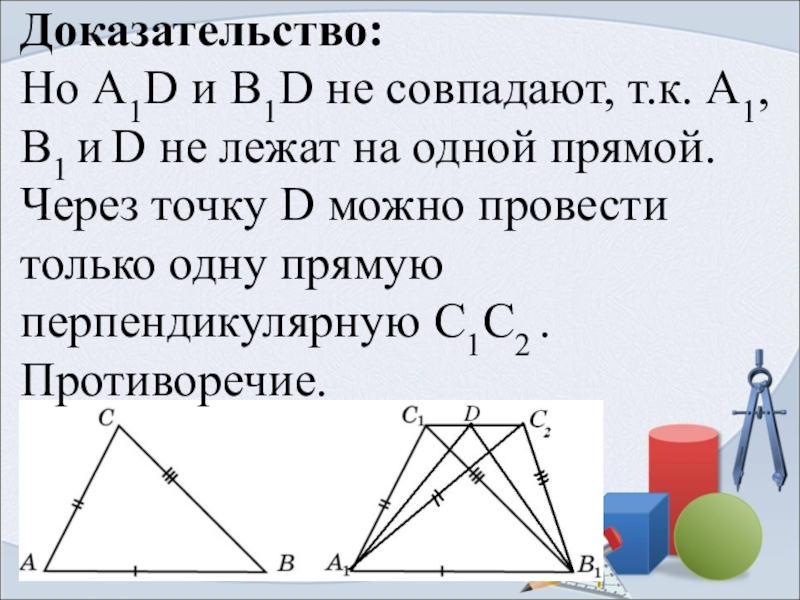
- 8. Доказательство: Но А1D и В1D не совпадают,
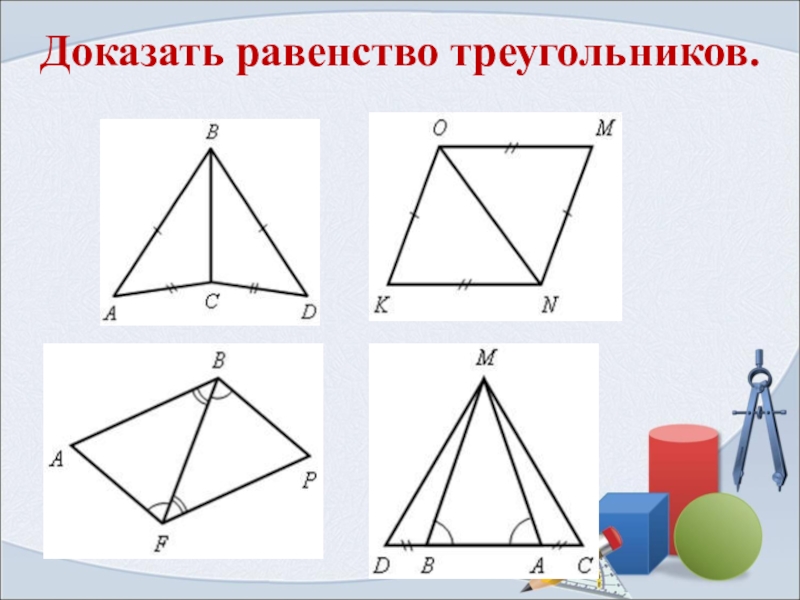
- 9. Доказать равенство треугольников.
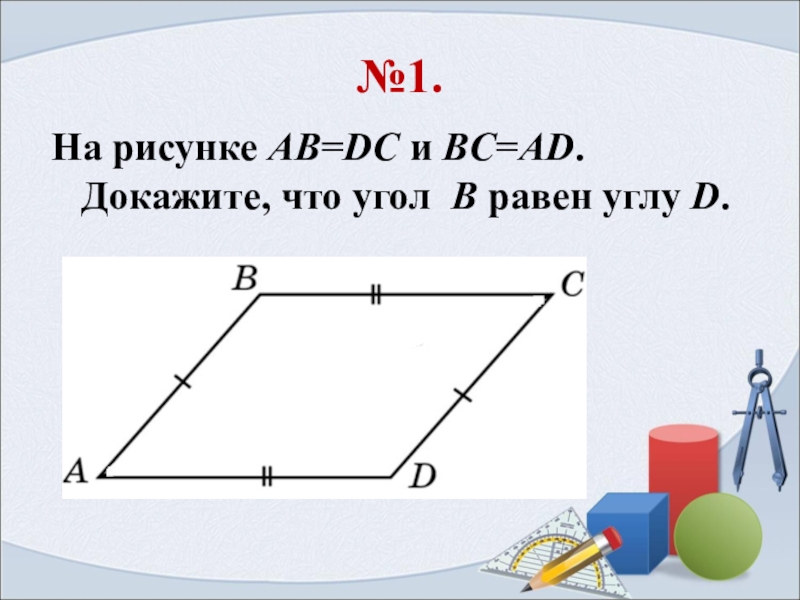
- 10. №1.На рисунке AB=DC и BC=AD. Докажите, что угол B равен углу D.
- 11. Дано: ΔАВС, ΔАDС, AB=DC, BC=AD.Доказать: ∠B =
- 12. №2.На рисунке AB=DC и BC=AD, уголBAC равен 31o, угол BCA равен 29o.Найдите угол ACD.
- 13. Решение: Треугольники ABC и CAD равны потретьему
- 14. №3.На рисунке АВ = AD и DC
- 15. Дано: ΔАСD, ΔАСB, AD=AB, DC=BC.Доказать: AC –
- 16. Домашнее задание.П.27, теорема 3.6.№29 (стр. 41)
- 17. СПАСИБО ЗА УРОК!
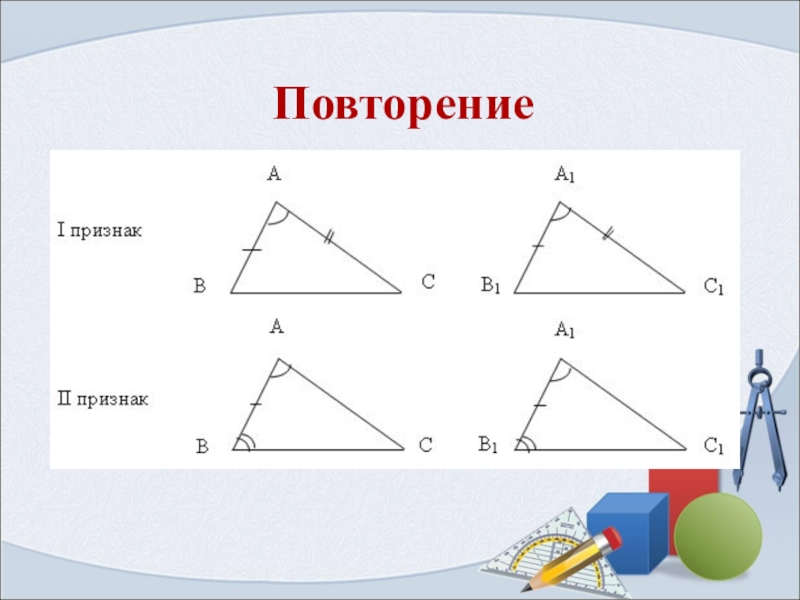
Повторение
Слайд 1Третий признак равенства
треугольников
Егорова Маргарита Владимировна
учитель математики
МБОУ Топкинская ООШ
с.Топки
Слайд 3Теорема 3.6.
Если три стороны одного треугольника соответственно равны трем сторонам другого
треугольника, то такие треугольники равны.
Слайд 5Доказательство: 1) Пусть ΔABC ≠ ΔA1B1C1, тогда ∠А≠∠A1, ∠В≠∠В1, ∠С≠∠С1 (иначе они были
бы равны по первому признаку).
Слайд 6Доказательство: 2) Пусть ΔABC2 = ΔA1B1C1. Пусть D∈C1C2, C1D = DC2. Тогда ΔAC1C2 и
ΔВС1C2 – равнобедренные с общим основанием С1C2 .
Слайд 7Доказательство: Поэтому их медианы А1D и В1D являются высотами. Значит А1D⊥ С1C2 и
В1D⊥ С1C2.
Слайд 8Доказательство: Но А1D и В1D не совпадают, т.к. А1, В1 и D
не лежат на одной прямой. Через точку D можно провести только одну прямую перпендикулярную С1C2 . Противоречие.
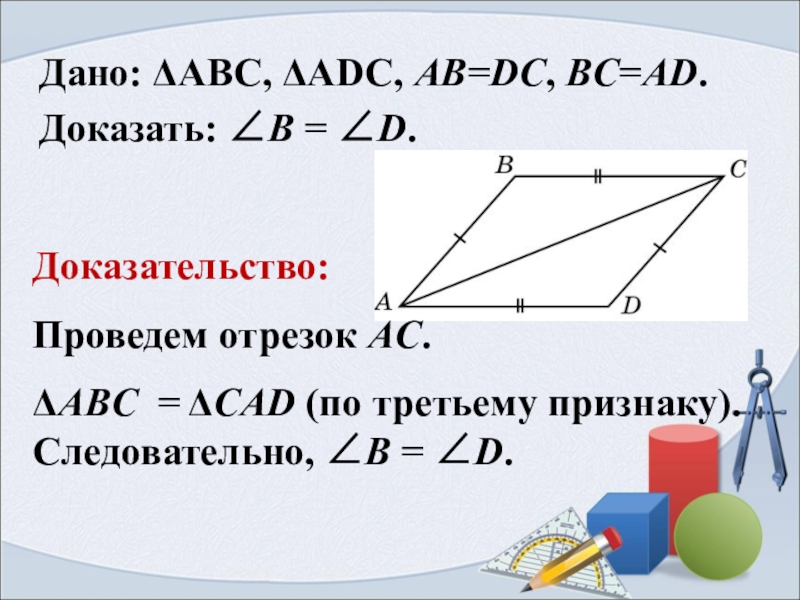
Слайд 11Дано: ΔАВС, ΔАDС, AB=DC, BC=AD.
Доказать: ∠B = ∠D.
Доказательство:
Проведем отрезок AC.
ΔABC = ΔCAD (по третьему признаку). Следовательно, ∠B = ∠D.
Слайд 13Решение:
Треугольники ABC и CAD равны по
третьему признаку.
Следовательно, угол ACD равен
углу
BAC и равен 31o.
Дано: ΔАВС, ΔАDС, ∠BAC=31o , ∠BCA=29o .
Найти: ∠BАС .
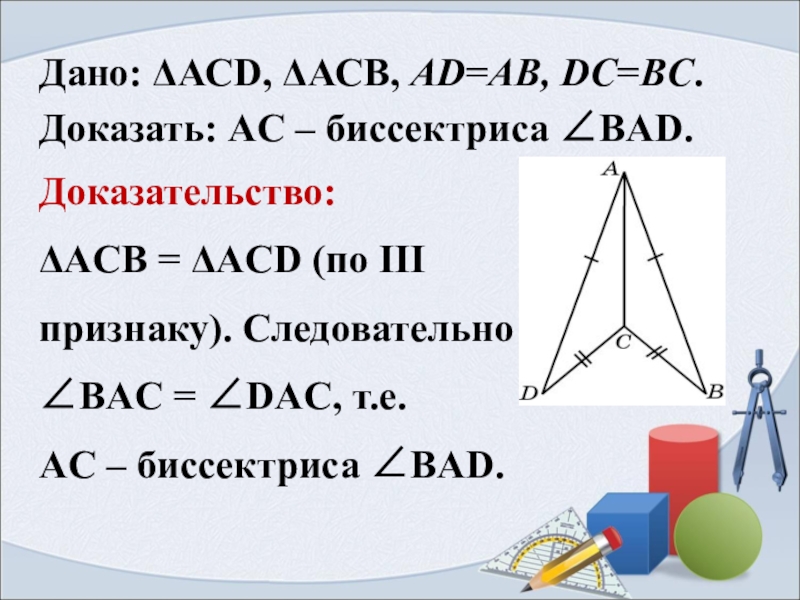
Слайд 15Дано: ΔАСD, ΔАСB, AD=AB, DC=BC.
Доказать: AC – биссектриса ∠BAD.
Доказательство:
ΔACB =
ΔACD (по III
признаку). Следовательно
∠BAC = ∠DAC, т.е.
AC – биссектриса ∠BAD.
признаку). Следовательно
∠BAC = ∠DAC, т.е.
AC – биссектриса ∠BAD.