- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 10 класс Аксиомы стереометрии, теория
Содержание
- 1. Презентация по геометрии 10 класс Аксиомы стереометрии, теория
- 2. Аксиоматический метод состоит в следующем: 1.
- 3. Слайд 3
- 4. Изображение пространственных фигурПересекаютсяПараллельныПерпендикулярныСкрещиваются
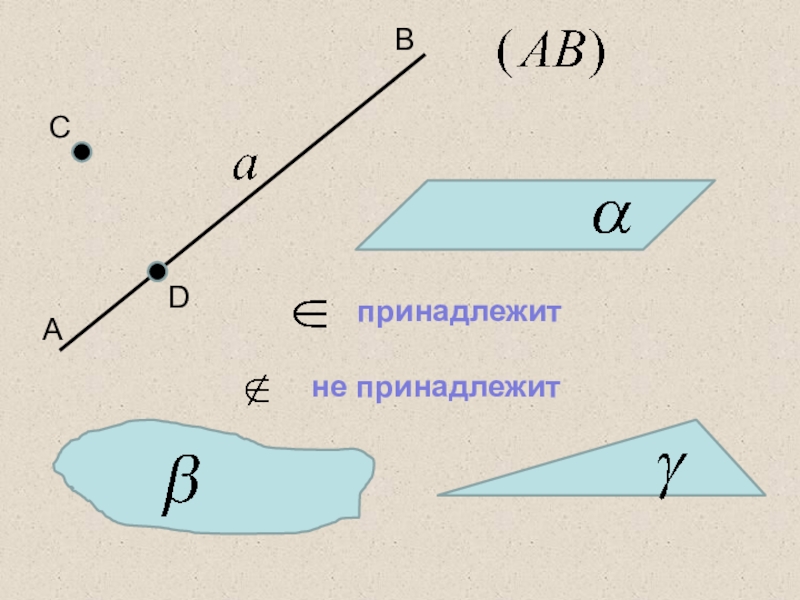
- 5. CABDпринадлежитне принадлежит
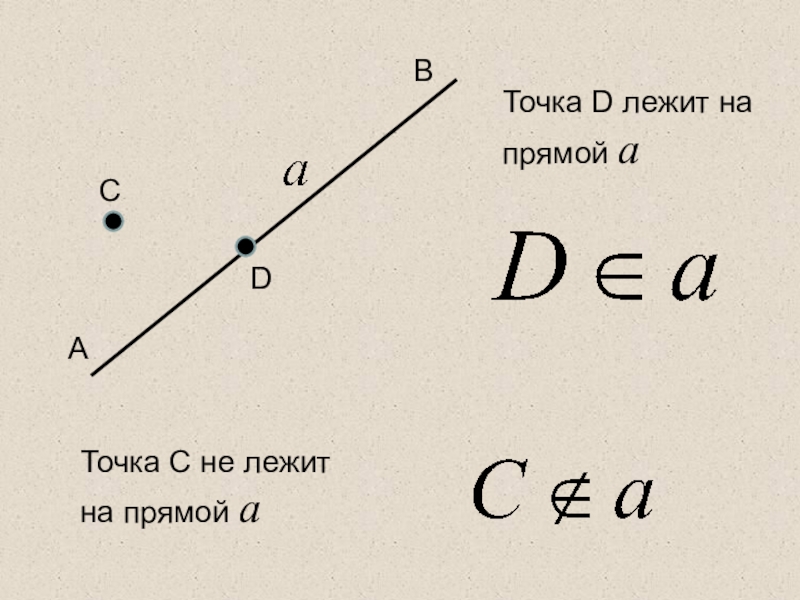
- 6. CABDТочка D лежит напрямой а Точка С не лежит на прямой а
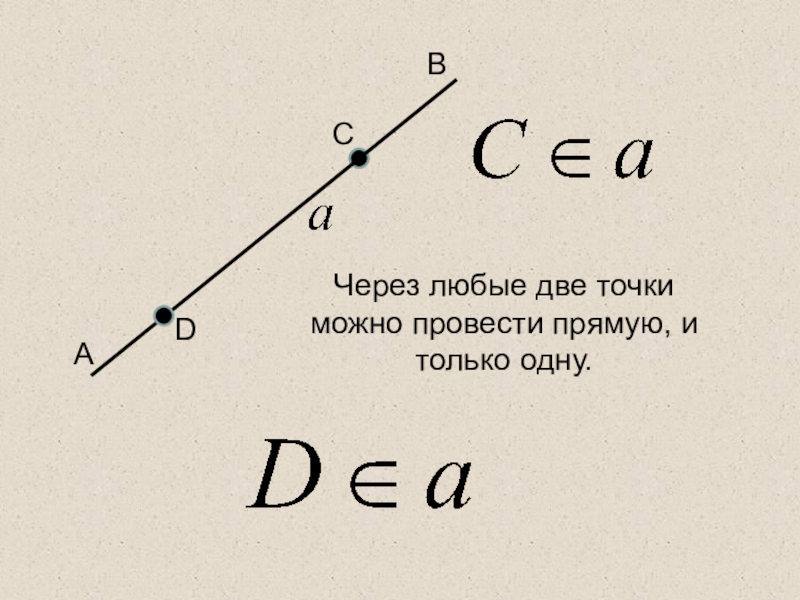
- 7. CABDЧерез любые две точки можно провести прямую, и только одну.
- 8. Аксиомы стереометрии 1) Какова бы ни
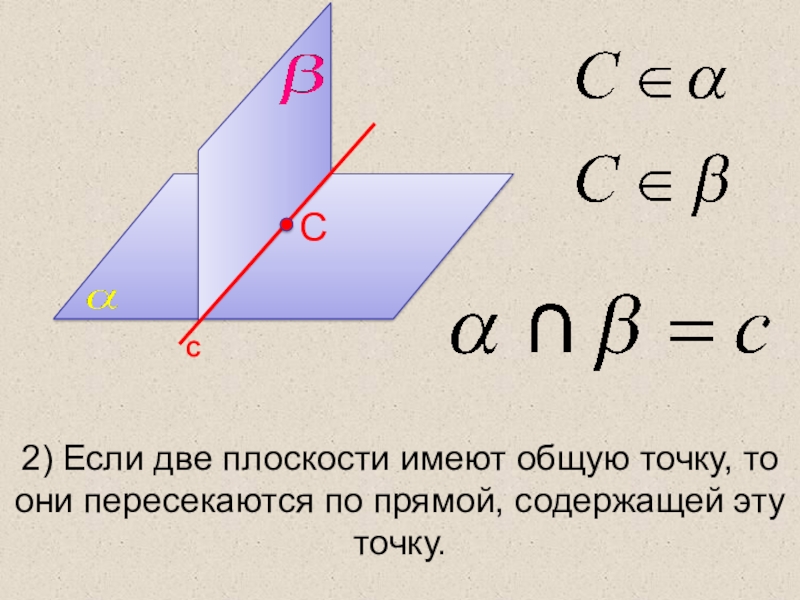
- 9. 2) Если две плоскости имеют общую точку, то они пересекаются по прямой, содержащей эту точку.СС
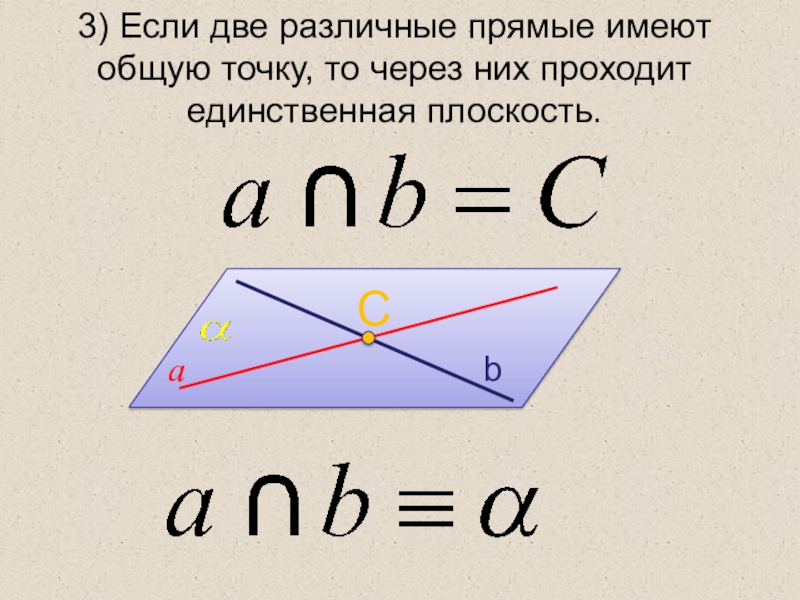
- 10. 3) Если две различные прямые имеют общую точку, то через них проходит единственная плоскость.аbC
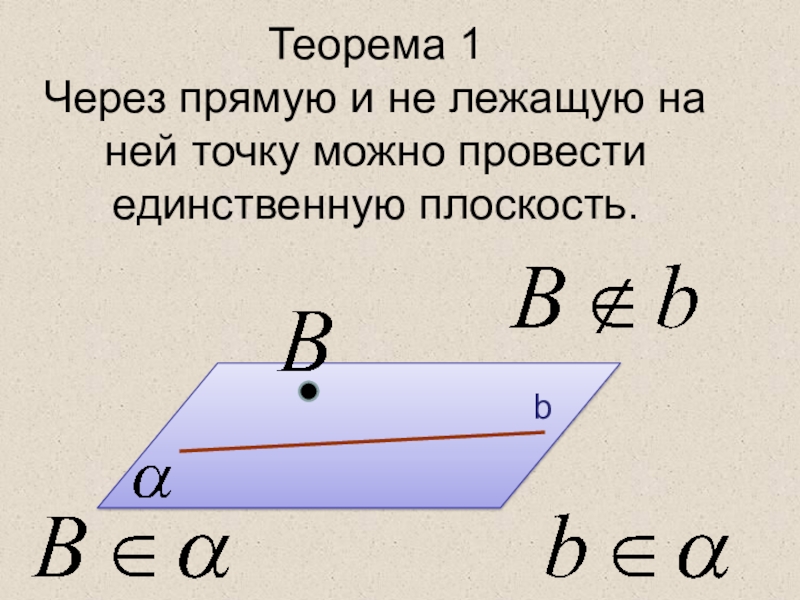
- 11. Теорема 1 Через прямую и не лежащую на ней точку можно провести единственную плоскость.
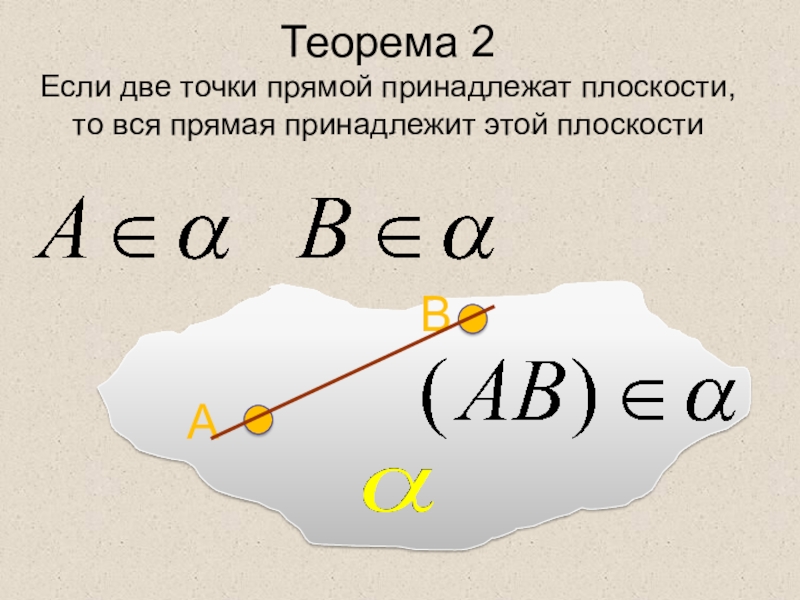
- 12. Теорема 2 Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости
- 13. Через три точки, не лежащие на одной прямой, можно провести единственную плоскость.Теорема 3
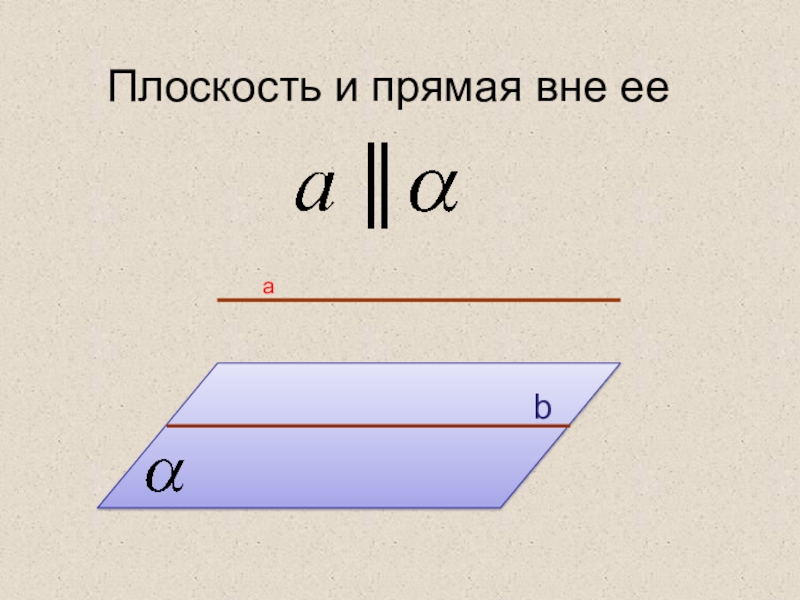
- 14. Плоскость и прямая вне ее а
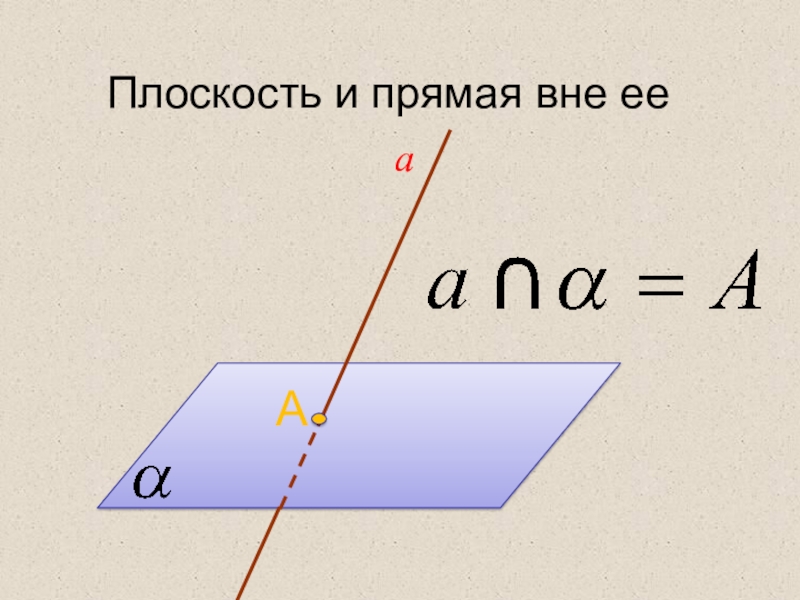
- 15. Плоскость и прямая вне ее аА
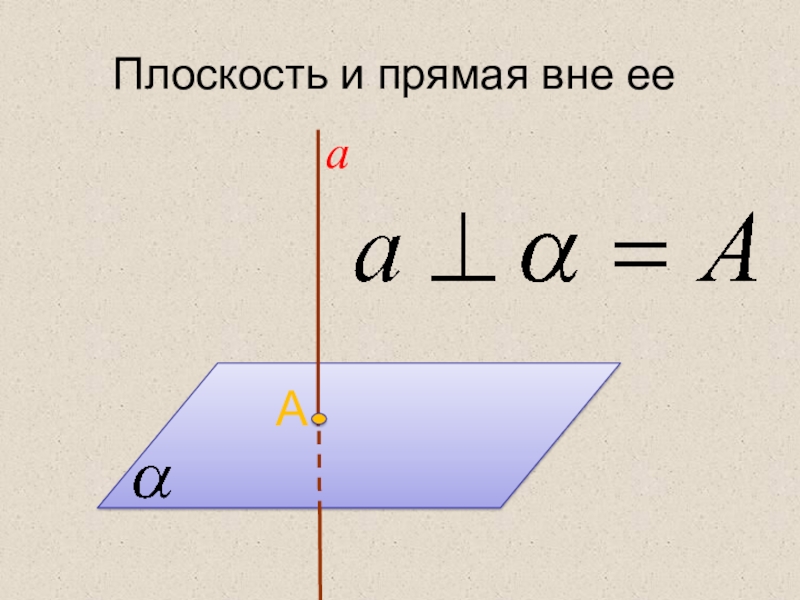
- 16. Плоскость и прямая вне ее аА
- 17. Способы задания плоскости:
Аксиоматический метод состоит в следующем: 1. Выявляют основные понятия изучаемой геометрии.2. Все понятия геометрии определяют через основные.3. Выбирают аксиомы – предложения, принимаемые без доказательства и составляющие основу для доказательства теорем. 4. Список аксиом должен быть
Слайд 2Аксиоматический метод состоит в следующем:
1. Выявляют основные понятия изучаемой геометрии.
2.
Все понятия геометрии определяют через основные.
3. Выбирают аксиомы – предложения, принимаемые без доказательства и составляющие основу для доказательства теорем.
4. Список аксиом должен быть таким, чтобы, опираясь на них, можно было получить необходимые выводы.
5. После того, как выделены основные понятия и сформулирован список аксиом, все дальнейшие утверждения (теоремы) выводятся чисто логическим путем.
Мы считаем основными понятиями точку, прямую и плоскость. Прямая и плоскость бесконечны.
3. Выбирают аксиомы – предложения, принимаемые без доказательства и составляющие основу для доказательства теорем.
4. Список аксиом должен быть таким, чтобы, опираясь на них, можно было получить необходимые выводы.
5. После того, как выделены основные понятия и сформулирован список аксиом, все дальнейшие утверждения (теоремы) выводятся чисто логическим путем.
Мы считаем основными понятиями точку, прямую и плоскость. Прямая и плоскость бесконечны.
Слайд 8Аксиомы стереометрии
1) Какова бы ни была плоскость, существуют точки, принадлежащие
этой плоскости и точки, не принадлежащие ей.
Слайд 92) Если две плоскости имеют общую точку, то они пересекаются по
прямой, содержащей эту точку.
С
С
Слайд 103) Если две различные прямые имеют общую точку, то через них
проходит единственная плоскость.
а
b
C
Слайд 12Теорема 2 Если две точки прямой принадлежат плоскости, то вся прямая принадлежит
этой плоскости
Слайд 13Через три точки, не лежащие на одной прямой, можно провести единственную
плоскость.
Теорема 3
Слайд 17 Способы задания плоскости: 1) две пересекающиеся прямые; 2)прямая, и не
лежащая на ней точка;
3) три точки, не лежащие на одной прямой;