кафедры математики и физики
Камчатского государственного университета имени Витуса Беринга,
кандидат педагогических наук, доцент,
г. Петропавловск - Камчатский
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Многогранники. Тела Платона. Тела Пуансо (10 класс)
Содержание
- 1. Презентация Многогранники. Тела Платона. Тела Пуансо (10 класс)
- 2. Многогранником называется совокупность таких плоских многоугольников, у
- 3. Выпуклым – называется такой многогранник, который остается
- 4. Пирамида – это многогранник, одна грань
- 5. Призма – многоугольник, две грани которого
- 6. Призматоид – многогранник, ограниченный двумя многоугольниками,
- 7. Итальянский учёный-францисканец Лука Пачоли на рубеже XV-XVI
- 8. Правильные многогранники «Правильных многогранников вызывающе
- 9. Названия правильных многогранников пришли
- 10. Тетраэдр – правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (это правильная треугольная пирамида).Тела Платона
- 11. Гексаэдр – правильный шестигранник Это куб состоящий из шести равных квадратов.
- 12. Октаэдр – правильный восьмигранник. Он состоит из
- 13. Додекаэдр – правильный двенадцатигранник, состоит из двенадцати
- 14. Икосаэдр – состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины
- 15. Этим красивым телам посвящена 13-я
- 16. Тетраэдр символизировал огонь, т.к. его вершина устремлена
- 17. Было выяснено, что правильных многогранников
- 18. Звездчатые формы вместе с правильными и
- 19. Это свойство тел, с одной стороны,
- 20. В Новое время Кеплер ввел
- 21. К звездчатым относятся и тела
- 22. Виды тел Пуансо
- 23. Малый звездчатый додекаэдр – звездчатый додекаэдр первого
- 24. Звездчатый октаэдр – восемь пересекающихся плоскостей граней
Многогранником называется совокупность таких плоских многоугольников, у которых каждая сторона одного является одновременно стороной другого (но только одного).Определение многогранника
Слайд 1презентация
«Многогранники. Тела платона. тела пуансо»
(10 класс)
Яковлева Татьяна Петровна,
доцент
Слайд 2Многогранником называется совокупность таких плоских многоугольников, у которых каждая сторона одного
является одновременно стороной другого (но только одного).
Определение многогранника
Слайд 3Выпуклым – называется такой многогранник, который остается по одну строну от
плоскости любой своей грани. В многограннике Кеплера оказалось 14 вершин, 24 грани и 36 ребер.
Слайд 4 Пирамида – это многогранник, одна грань которого многоугольник, а остальные
грани – треугольники с общей вершиной.
Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника.
Пирамида называется усеченной, если вершина её отсекается плоскостью.
Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника.
Пирамида называется усеченной, если вершина её отсекается плоскостью.
Слайд 5 Призма – многоугольник, две грани которого (основания призмы) представляют собой
равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы.
Призма называется прямой, если её ребра перпендикулярны плоскости основания.
Если основанием призмы является прямоугольник, призму называют параллелепипедом.
Призма называется прямой, если её ребра перпендикулярны плоскости основания.
Если основанием призмы является прямоугольник, призму называют параллелепипедом.
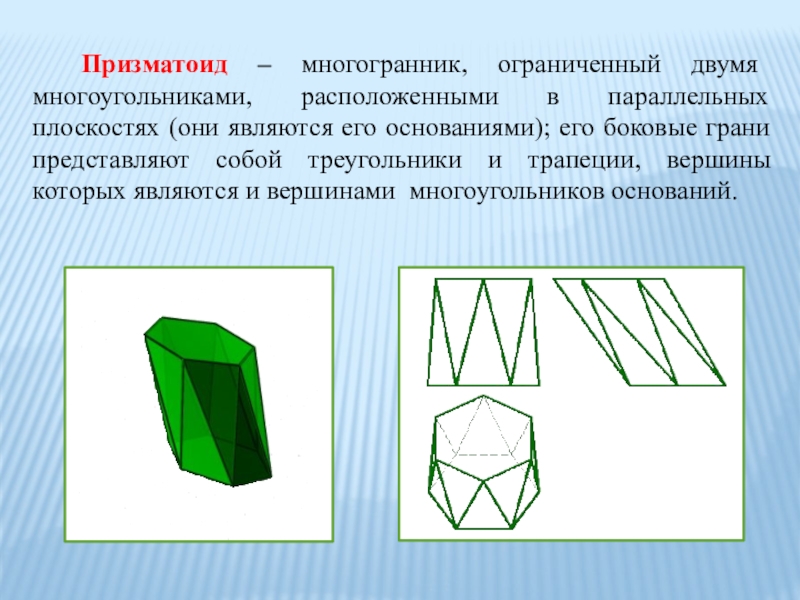
Слайд 6 Призматоид – многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях
(они являются его основаниями); его боковые грани представляют собой треугольники и трапеции, вершины которых являются и вершинами многоугольников оснований.
Слайд 7Итальянский учёный-францисканец Лука Пачоли на рубеже XV-XVI вв. писал и публиковал
математические труды, которые иллюстрировал, в том числе, Леонардо да Винчи. На портрете Пачоли (он в центре, а автор - не Леонардо да Винчи) - многогранники (один стеклянный, наполовину полон водой).
Слайд 8Правильные многогранники
«Правильных многогранников вызывающе мало», – написал когда-то
Л. Кэрролл, – «но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук».
Л. Кэрролл
Слайд 9
Названия правильных многогранников пришли из Греции. В дословном переводе с
греческого «тетраэдр», «октаэдр», «гексаэдр», «додекаэдр», «икосаэдр» означают: «четырехгранник», «восьмигранник», «шестигранник», «двенадцатигранник», «двадцатигранник».
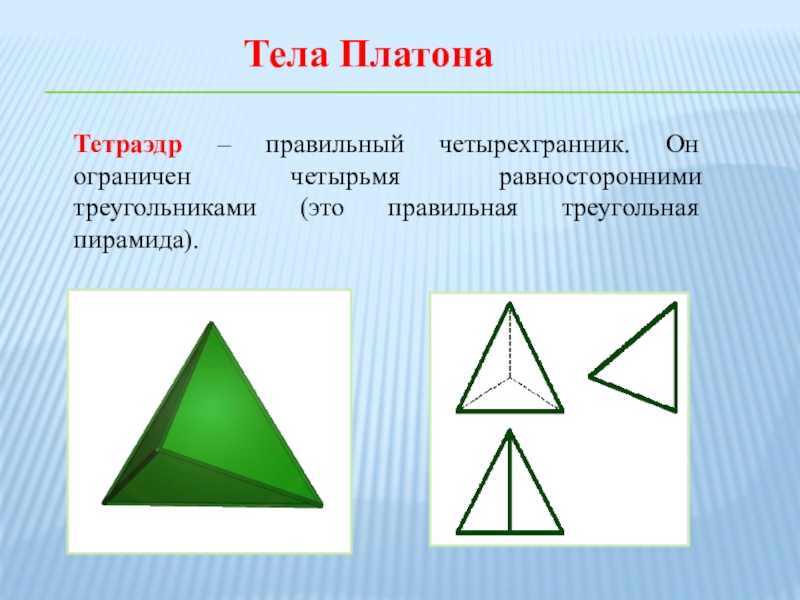
Слайд 10Тетраэдр – правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (это правильная
треугольная пирамида).
Тела Платона
Слайд 12Октаэдр – правильный восьмигранник. Он состоит из восьми равносторонних и равных
между собой треугольников, соединенных по четыре у каждой вершины.
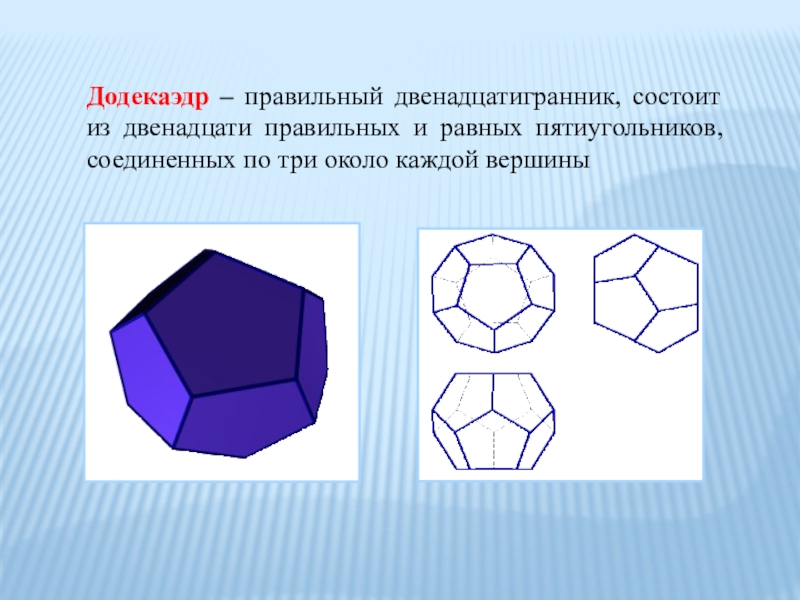
Слайд 13Додекаэдр – правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников,
соединенных по три около каждой вершины
Слайд 14Икосаэдр – состоит из 20 равносторонних и равных треугольников, соединенных по
пять около каждой вершины
Слайд 15 Этим красивым телам посвящена 13-я книга "Начал" Евклида. Их
еще называют телами Платона, т.к. они занимали важное место в философской концепции Платона об устройстве мироздания. Четыре многогранника олицетворяли в ней четыре сущности или "стихии".
Евклид
Слайд 16Тетраэдр символизировал огонь, т.к. его вершина устремлена вверх.
Икосаэдр - воду, т.к.
он самый "обтекаемый"; куб - землю, как самый "устойчивый".
Октаэдр - воздух, как самый "воздушный".
Декаэдр, воплощал в себе "все сущее", символизировал все мироздание, считался главным.
Октаэдр - воздух, как самый "воздушный".
Декаэдр, воплощал в себе "все сущее", символизировал все мироздание, считался главным.
Слайд 17 Было выяснено, что правильных многогранников ровно пять. Знаменитый математик
Л. Эйлер получил формулу :
В+Г-Р=2,
которая связывает число вершин /В/, граней /Г/ и ребер /Р/ любого многогранника.
Простота этой формулы заключается в том, что она не связана ни с расстоянием, ни с углами.
В+Г-Р=2,
которая связывает число вершин /В/, граней /Г/ и ребер /Р/ любого многогранника.
Простота этой формулы заключается в том, что она не связана ни с расстоянием, ни с углами.
ФОРМУЛА Л.ЭЙЛЕРА: В+Г-Р=2
Л. Эйлер
Слайд 18 Звездчатые формы вместе с правильными и полуправильными телами образуют 66
тел.
Это число почти удвоится, если к ним добавить невыпуклые однородные многогранники, у которых часть граней, состоящая из правильных многоугольников, является выпуклой, а часть оказывается вдавленной внутрь объема.
Это число почти удвоится, если к ним добавить невыпуклые однородные многогранники, у которых часть граней, состоящая из правильных многоугольников, является выпуклой, а часть оказывается вдавленной внутрь объема.
Звездчатые формы многогранника
Слайд 19 Это свойство тел, с одной стороны, роднит их с правильными
и полуправильными телами, а с другой — объединяет и со звездчатыми телами, которые могут покоиться на плоскости, только опираясь на несколько вершин или ребер.
Особый класс образуют параллелоэдры, которыми можно заполнить все бесконечное пространство, не оставляя пустоты и без того, чтобы их внутренние объемы пересекались.
Особый класс образуют параллелоэдры, которыми можно заполнить все бесконечное пространство, не оставляя пустоты и без того, чтобы их внутренние объемы пересекались.
Слайд 20 В Новое время Кеплер ввел звездчатый октаэдр, который получался
в результате взаимного проникновение двух тетраэдров, построенных внутри куба.
У него получилось, что из каждой грани одного тетраэдра торчит вершина другого тетраэдра в форме трехгранной пирамиды.
Эта фигура уже не относится к выпуклым многогранникам, так как ее невозможно поставить, скажем, на стол одной какой-то гранью.
У него получилось, что из каждой грани одного тетраэдра торчит вершина другого тетраэдра в форме трехгранной пирамиды.
Эта фигура уже не относится к выпуклым многогранникам, так как ее невозможно поставить, скажем, на стол одной какой-то гранью.
Звездчатый октаэдр
Кеплер
Слайд 21 К звездчатым относятся и тела Пуансо, у которых имеются
самопересекающиеся грани. Они, как и звезда Кеплера, не противоречат определению многогранника, а это определение требует, чтобы каждое ребро многогранника разделяло две и только две грани.
Тела Пуансо
Пуансо
Слайд 23Малый звездчатый додекаэдр – звездчатый додекаэдр первого продолжения. Каждая грань выпуклого
додекаэдра при продолжении образует правильный звездчатый пятиугольник. Пересекающиеся плоскости граней додекаэдра отделяют от пространства новые «куски», внешние по отношению к додекаэдру.
Слайд 24Звездчатый октаэдр – восемь пересекающихся плоскостей граней октаэдра отделяют от пространства
новые «куски», внешние по отношению к октаэдру. Это малые тетраэдры основания которые совпадают с гранями октаэдра.