- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Касательная к окружности
Содержание
- 1. Презентация Касательная к окружности
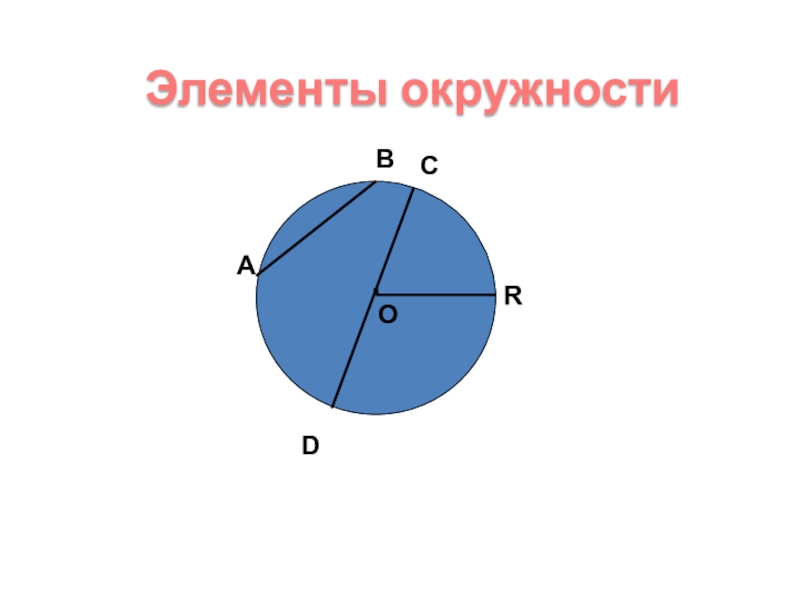
- 2. Элементы окружности .ОАВСDR
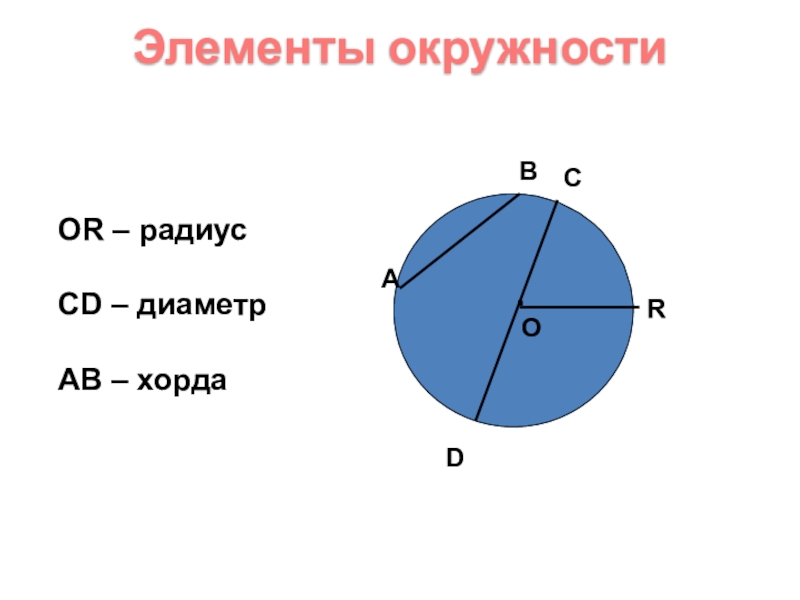
- 3. Элементы окружности .ОАВСDRОR – радиусСD – диаметрAB – хорда
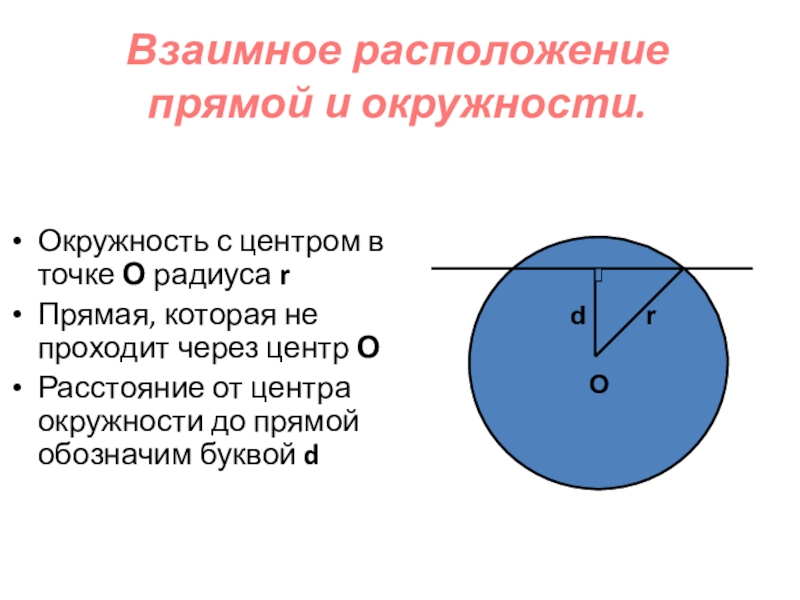
- 4. Взаимное расположение прямой и окружности.Окружность с центром
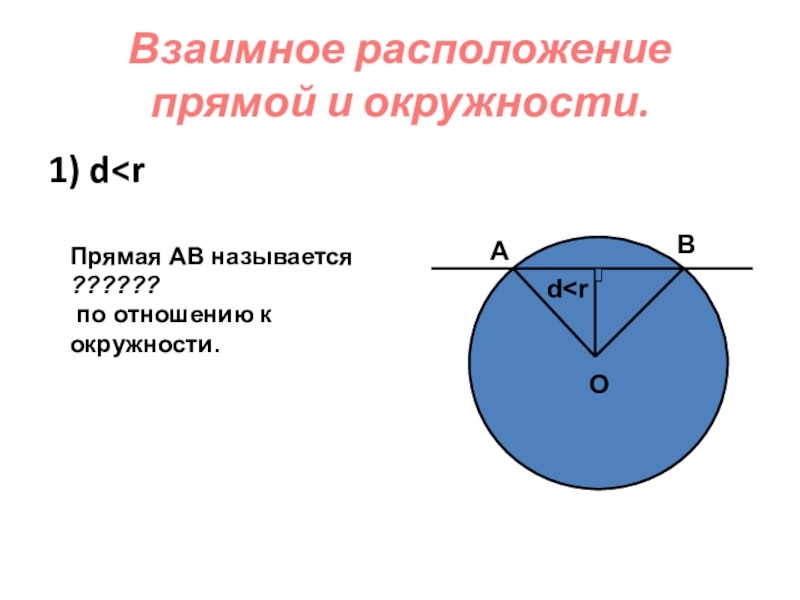
- 5. Взаимное расположение прямой и окружности.1) d
- 6. 2) d=rOd=rM Прямая, имеющая с окружностью только
- 7. Взаимное расположение прямой и окружности.3) d>rЕсли расстояние
- 8. Выясните взаимное расположение прямой и окружности, если:
- 9. Выясните взаимное расположение прямой и окружности, если:
- 10. 1. Окружность и прямая имеют две
- 11. 2. Закончите фразу, чтобы получилось верное высказывание Окружность и прямая имеют одну общую точку, если...
- 12. 3. Установите истинность или ложность следующих утверждений:
- 13. №633
- 14. Касательная к окружности АОр
- 15. Касательная к окружности перпендикулярна к радиусу,
- 16. Если прямая проходит через конец радиуса,
- 17. Отрезки касательных к окружности,
- 18. ▼ По свойству касательной ∆АВО, ∆АСО–прямоугольные∆АВО=∆АСО–по гипотенузе
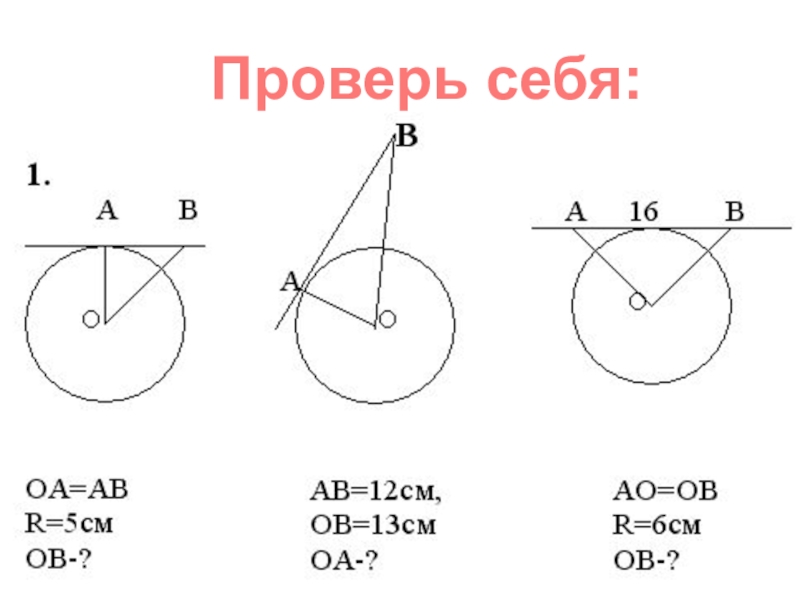
- 19. Проверь себя:
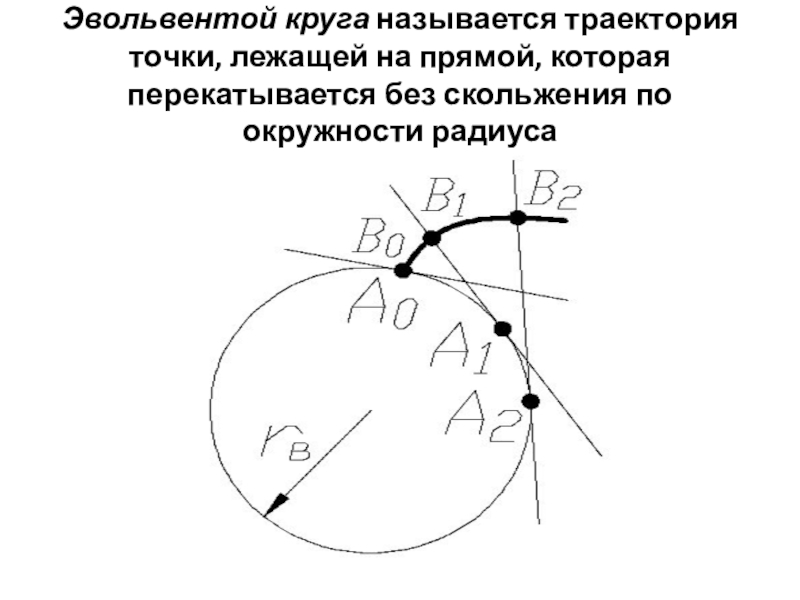
- 20. Эвольвентой круга называется траектория точки, лежащей на прямой, которая перекатывается без скольжения по окружности радиуса
- 21. Капли дождя движутся по касательной к циклоиде
- 22. А что нужно сделать, чтобы тело стало искусственным спутником Земли?
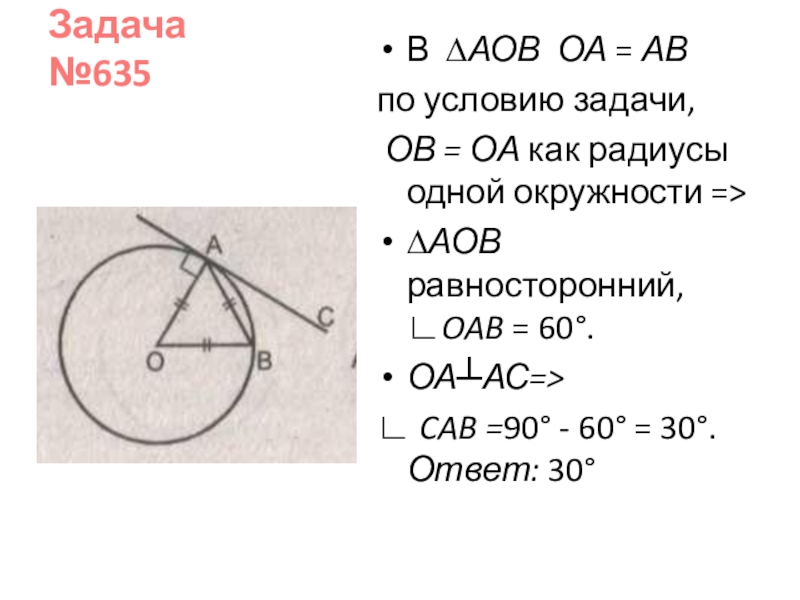
- 23. Задача №635 В ∆АОВ ОА = АВ
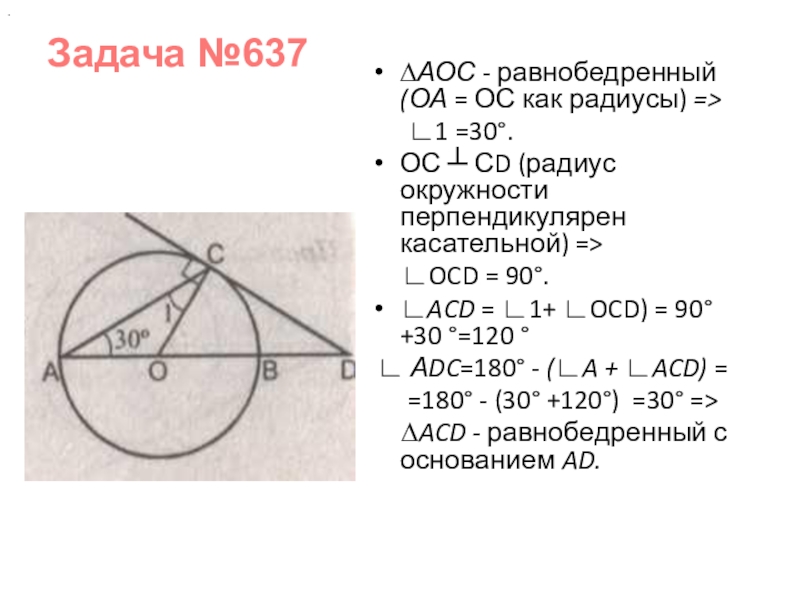
- 24. . ∆АОС - равнобедренный (ОА = ОС
- 25. Домашнее задание. П. 69, страница
- 26. Что вы узнали нового на уроке?
Элементы окружности .ОАВСDR
Слайд 4Взаимное расположение прямой и окружности.
Окружность с центром в точке О радиуса
r
Прямая, которая не проходит через центр О
Расстояние от центра окружности до прямой обозначим буквой d
Прямая, которая не проходит через центр О
Расстояние от центра окружности до прямой обозначим буквой d
O
r
d
Слайд 6
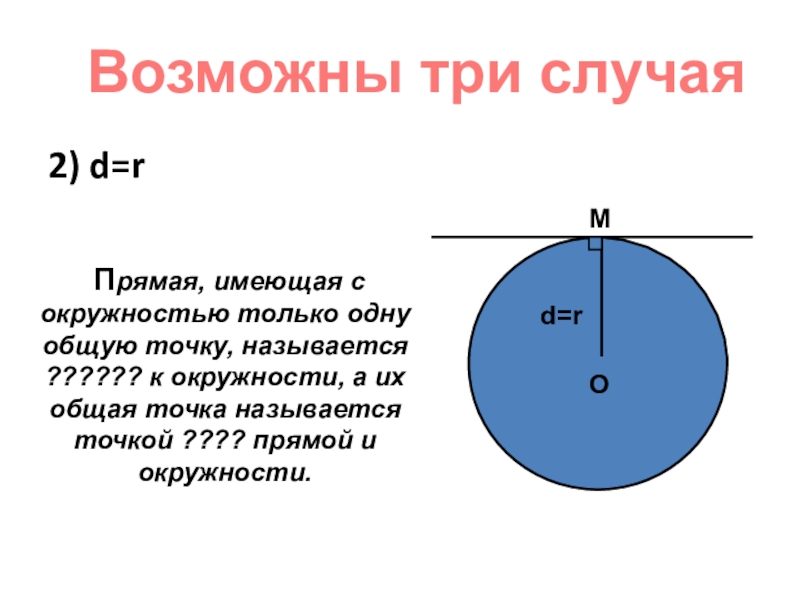
2) d=r
O
d=r
M
Прямая, имеющая с окружностью только одну общую точку, называется
?????? к окружности, а их общая точка называется точкой ???? прямой и окружности.
Возможны три случая
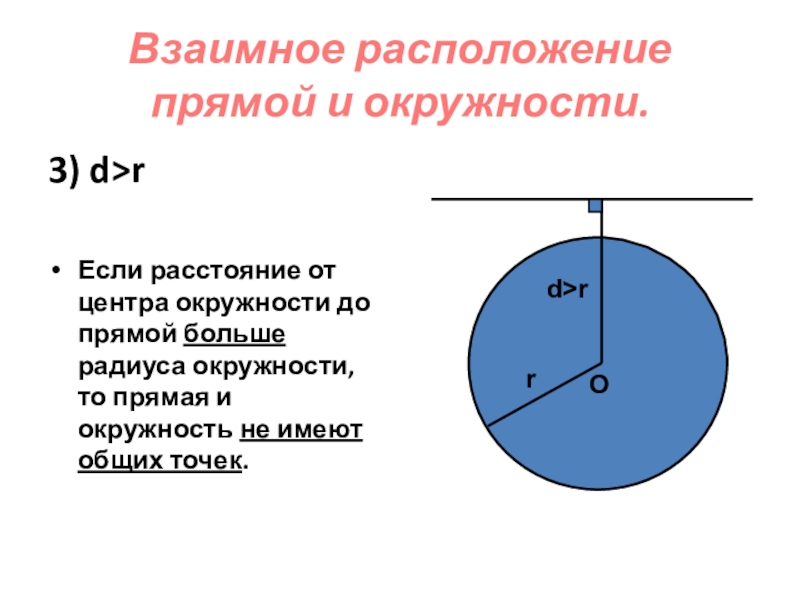
Слайд 7Взаимное расположение прямой и окружности.
3) d>r
Если расстояние от центра окружности до
прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
O
d>r
r
Слайд 8Выясните взаимное расположение прямой и окружности, если:
r = 15 см, d
= 11см
r = 6 см, d = 5,2 см
r = 3,2 м, d = 4,7 м
r = 7 см, d = 0,5 дм
r = 4 см, d = 40 мм
r = 6 см, d = 5,2 см
r = 3,2 м, d = 4,7 м
r = 7 см, d = 0,5 дм
r = 4 см, d = 40 мм
Слайд 9Выясните взаимное расположение прямой и окружности, если:
r = 15 см, d
= 11см
r = 6 см, d = 5,2 см
r = 3,2 м, d = 4,7 м
r = 7 см, d = 0,5 дм
r = 4 см, d = 40 мм
r = 6 см, d = 5,2 см
r = 3,2 м, d = 4,7 м
r = 7 см, d = 0,5 дм
r = 4 см, d = 40 мм
прямая – секущая
прямая – секущая
общих точек нет
прямая – секущая
прямая - касательная
Слайд 10
1. Окружность и прямая имеют две общие точки, если:
а) расстояние от центра
окружности до прямой не превосходит радиуса окружности;
б) расстояние от центра окружности до прямой меньше радиуса окружности;
в) расстояние от окружности до прямой меньше радиуса окружности.
б) расстояние от центра окружности до прямой меньше радиуса окружности;
в) расстояние от окружности до прямой меньше радиуса окружности.
и
Среди следующих утверждений укажите истинные.
Слайд 112. Закончите фразу, чтобы получилось верное высказывание
Окружность и прямая имеют одну
общую точку, если...
Слайд 123. Установите истинность или ложность следующих утверждений:
а) Прямая а является секущей
по отношению к окружности, если она имеет с окружностью общие точки.
б) Прямая а является секущей по отношению к окружности, если она пересекает окружность в двух точках.
в) Прямая а является секущей по отношению к окружности, если расстояние от центра окружности до данной прямой не больше радиуса.
б) Прямая а является секущей по отношению к окружности, если она пересекает окружность в двух точках.
в) Прямая а является секущей по отношению к окружности, если расстояние от центра окружности до данной прямой не больше радиуса.
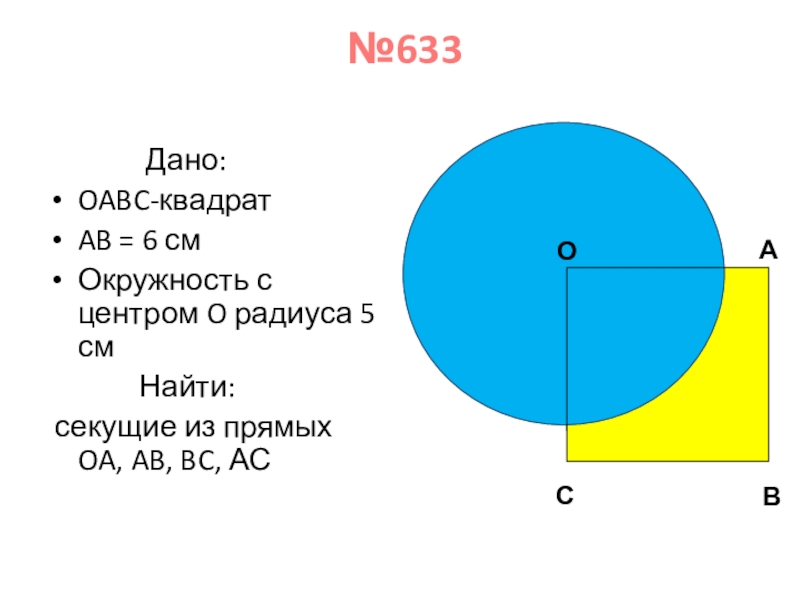
Слайд 13 №633
Дано:
OABC-квадрат
AB = 6
см
Окружность с центром O радиуса 5 см
Найти:
секущие из прямых OA, AB, BC, АС
Окружность с центром O радиуса 5 см
Найти:
секущие из прямых OA, AB, BC, АС
О
А
В
С
О
Слайд 15
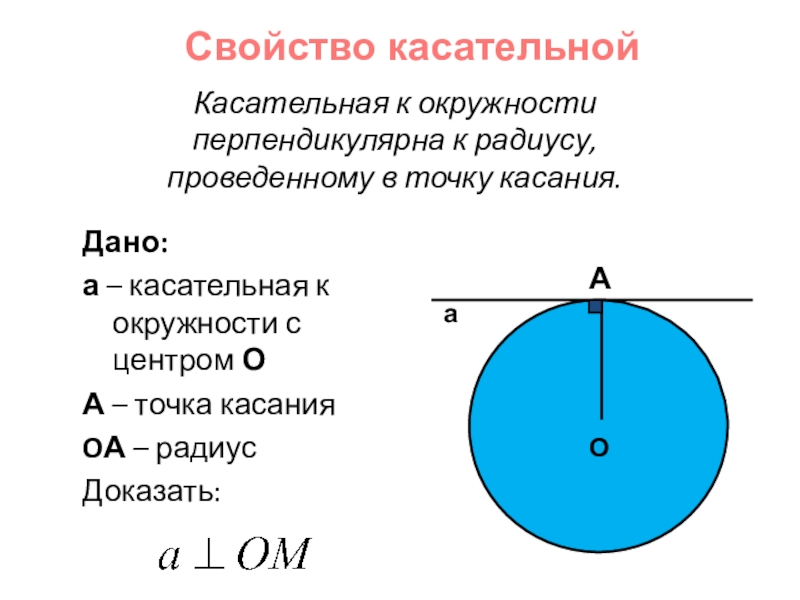
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Дано:
а –
касательная к окружности с центром О
А – точка касания
OА – радиус
Доказать:
А – точка касания
OА – радиус
Доказать:
O
А
а
Свойство касательной
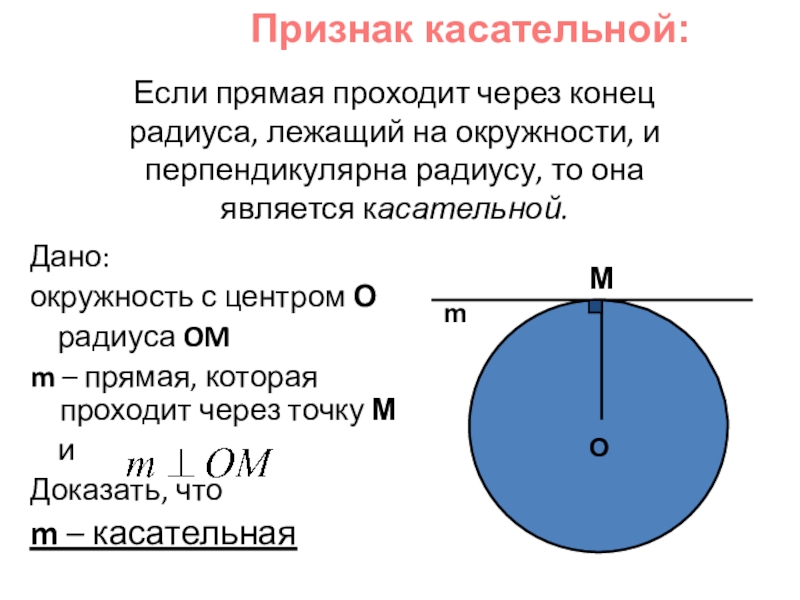
Слайд 16 Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна
радиусу, то она является касательной.
Дано:
окружность с центром О
радиуса OM
m – прямая, которая проходит через точку М
и
Доказать, что
m – касательная
O
M
m
Признак касательной:
Слайд 17
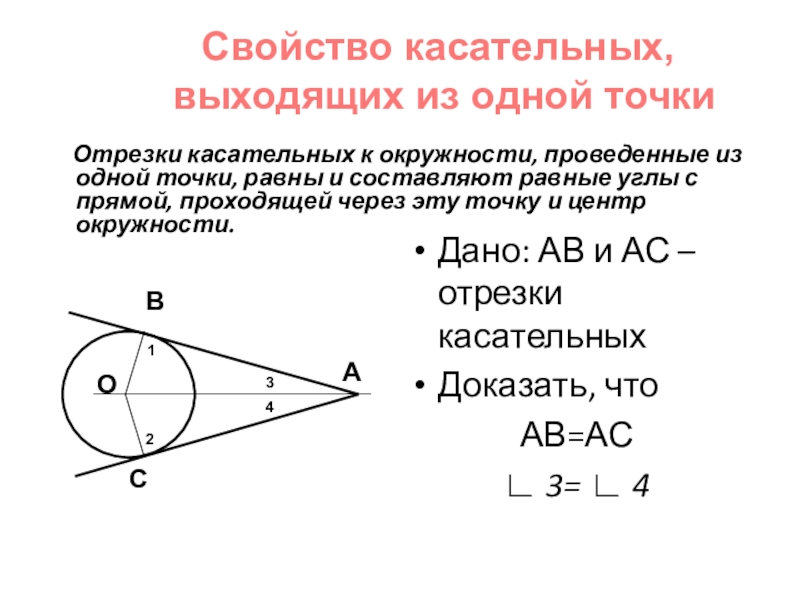
Отрезки касательных к окружности, проведенные из одной точки,
равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Дано: АВ и АС – отрезки касательных
Доказать, что
АВ=АС
∟ 3= ∟ 4
О
В
С
А
1
2
3
4
Свойство касательных,
выходящих из одной точки
Слайд 18
▼ По свойству касательной
∆АВО, ∆АСО–прямоугольные
∆АВО=∆АСО–по гипотенузе и катету:
ОА –
общая,
ОВ=ОС – радиусы
АВ=АС и
▲
ОВ=ОС – радиусы
АВ=АС и
▲
О
В
С
А
1
2
3
4
Свойство касательных,
выходящих из одной точки
Слайд 20Эвольвентой круга называется траектория точки, лежащей на прямой, которая перекатывается без
скольжения по окружности радиуса
Слайд 21Капли дождя движутся по касательной к циклоиде – кривой которую описывает
точка на ободе катящегося колеса
Слайд 23Задача №635
В ∆АОВ ОА = АВ
по условию задачи,
ОВ =
ОА как радиусы одной окружности =>
∆АОВ равносторонний, ∟OAB = 60°.
ОА┴АС=>
∟ CAB =90° - 60° = 30°. Ответ: 30°
∆АОВ равносторонний, ∟OAB = 60°.
ОА┴АС=>
∟ CAB =90° - 60° = 30°. Ответ: 30°
Слайд 24.
∆АОС - равнобедренный (ОА = ОС как радиусы) =>
∟1 =30°.
ОС ┴ СD (радиус окружности перпендикулярен касательной) =>
∟OCD = 90°.
∟ACD = ∟1+ ∟OCD) = 90°+30 °=120 °
∟ АDC=180° - (∟A + ∟ACD) =
=180° - (30° +120°) =30° =>
∆ACD - равнобедренный с основанием AD.
ОС ┴ СD (радиус окружности перпендикулярен касательной) =>
∟OCD = 90°.
∟ACD = ∟1+ ∟OCD) = 90°+30 °=120 °
∟ АDC=180° - (∟A + ∟ACD) =
=180° - (30° +120°) =30° =>
∆ACD - равнобедренный с основанием AD.
Задача №637
