- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Решение задач по теме Признаки равенства треугольников (7 класс)
Содержание
- 1. Презентация к уроку Решение задач по теме Признаки равенства треугольников (7 класс)
- 2. Слайд 2
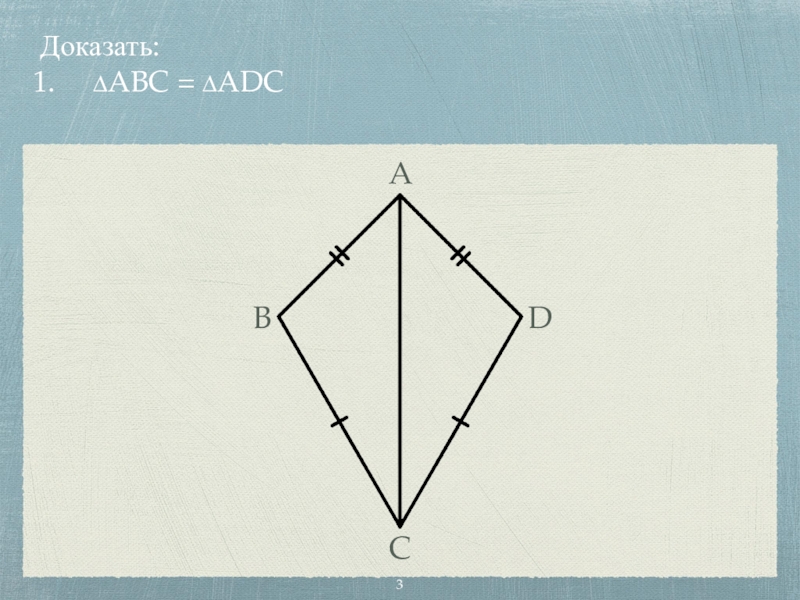
- 3. Доказать: ∆ABC = ∆ADC ABCD
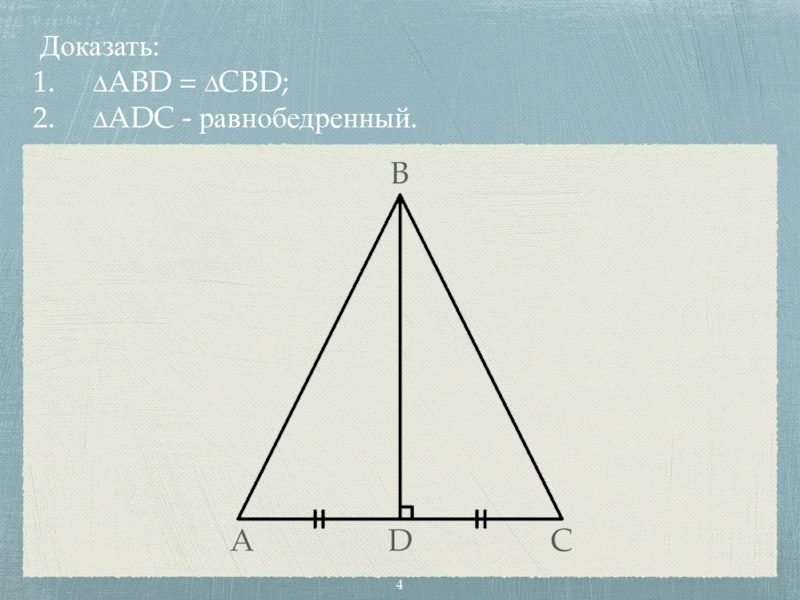
- 4. Доказать: ∆ABD = ∆CBD; ∆ADC - равнобедренный.BADC
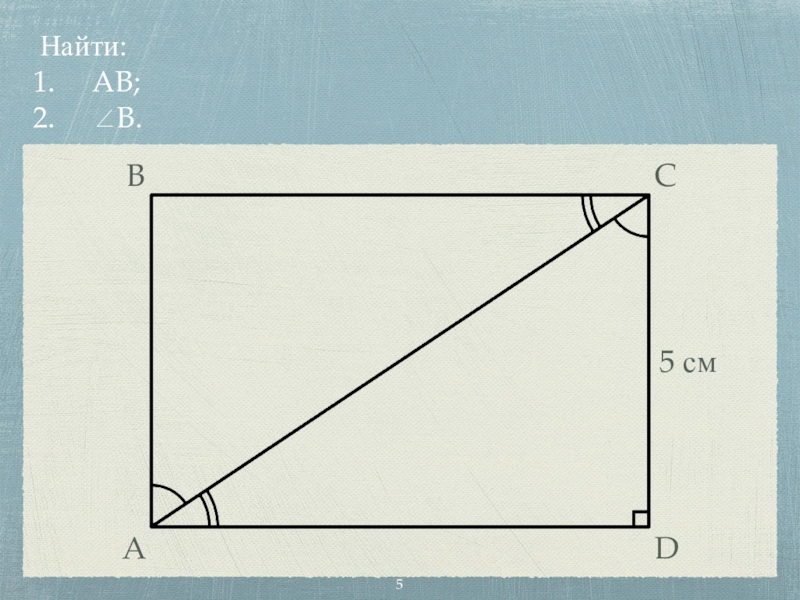
- 5. Найти: AB; ∠B.BADC5 см
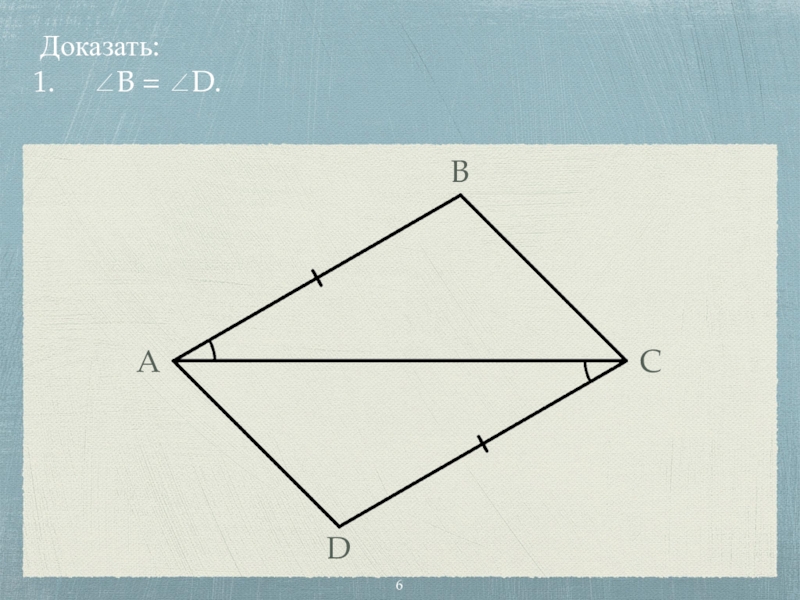
- 6. Доказать: ∠B = ∠D. BADC
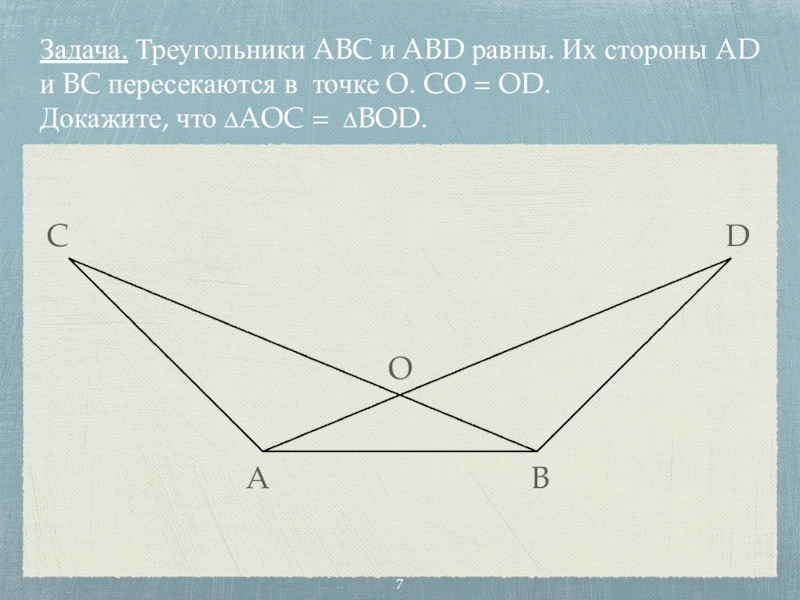
- 7. Задача. Треугольники ABC и ABD равны. Их
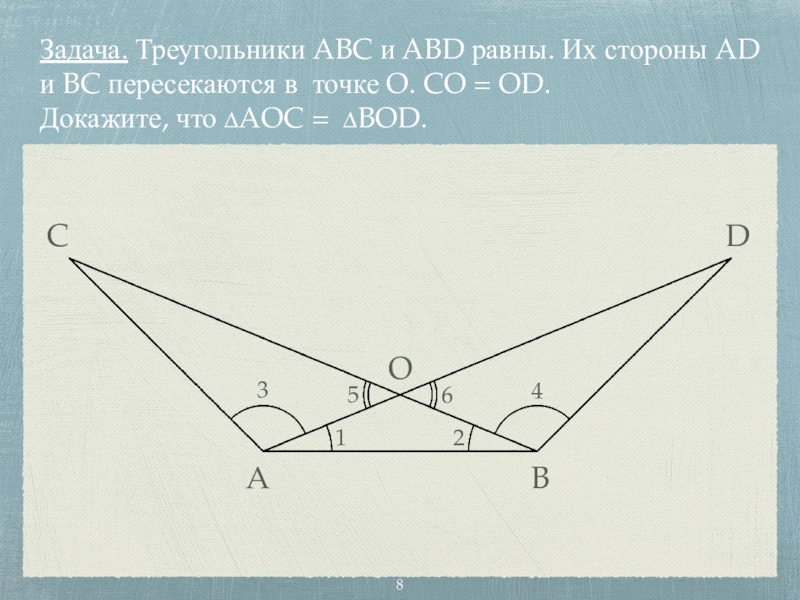
- 8. Задача. Треугольники ABC и ABD равны. Их
- 9. Дано: ∆ABC = ∆ABD. AC = BD;
- 10. Слайд 10
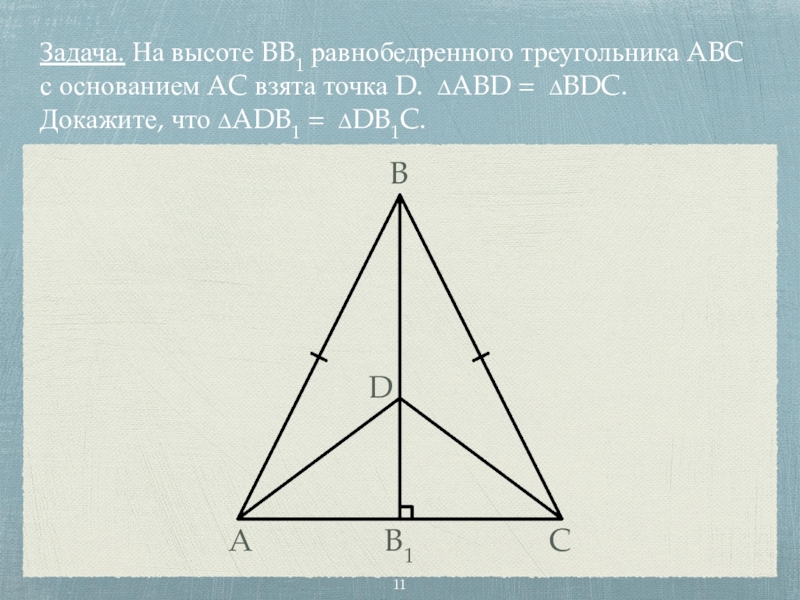
- 11. Задача. На высоте BB1 равнобедренного треугольника ABC
- 12. Спасибо за внимание!
Доказать: ∆ABC = ∆ADC ABCD
Слайд 1Решение задач по теме
“ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ”
Решение одной задачи разными способами
Слайд 7Задача. Треугольники ABC и ABD равны. Их стороны AD и BC
пересекаются в точке O. CO = OD.
Докажите, что ∆AOC = ∆BOD.
Докажите, что ∆AOC = ∆BOD.
B
A
D
C
O
Слайд 8Задача. Треугольники ABC и ABD равны. Их стороны AD и BC
пересекаются в точке O. CO = OD.
Докажите, что ∆AOC = ∆BOD.
Докажите, что ∆AOC = ∆BOD.
B
A
D
C
O
1
2
3
4
6
5
Слайд 9Дано: ∆ABC = ∆ABD.
AC = BD;
BC = AD;
AB
- общая;
CO = OD;
∠1 = ∠2;
∠BAC = ∠ABD;
∠C = ∠D.
CO = OD;
∠1 = ∠2;
∠BAC = ∠ABD;
∠C = ∠D.
Значит:
AO = BO;
AO = AD - OD,
BO = BC - OC.
∠3 = ∠4;
∠3 = ∠BAC - ∠1,
∠4 = ∠ABD - ∠2.
∠5 = ∠6.
вертикальные
Слайд 11Задача. На высоте BB1 равнобедренного треугольника ABC с основанием AC взята
точка D. ∆ABD = ∆BDC.
Докажите, что ∆ADB1 = ∆DB1C.
Докажите, что ∆ADB1 = ∆DB1C.
B
A
B1
C
D