- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Прямоугольный параллелепипед.
Содержание
- 1. Презентация к уроку Прямоугольный параллелепипед.
- 2. Название «параллелепипед» происходит от греческого слова «параллелос»,
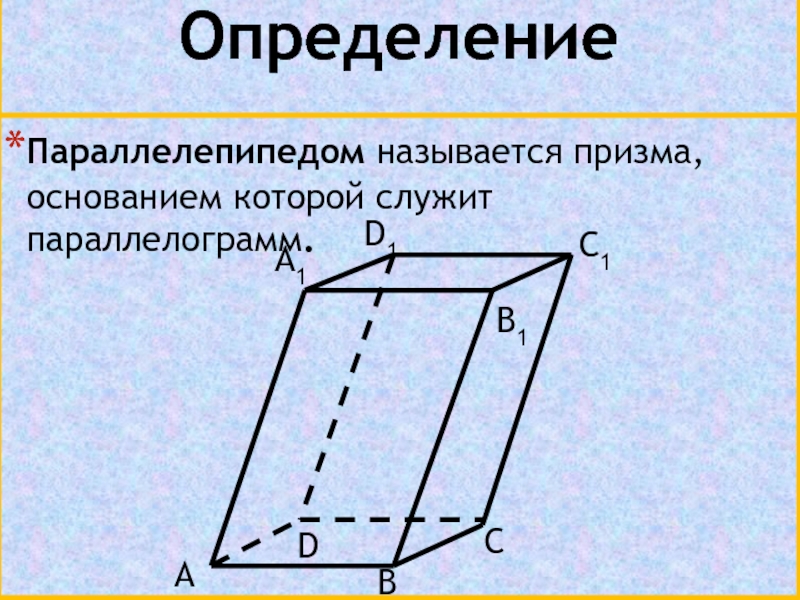
- 3. ОпределениеПараллелепипедом называется призма, основанием которой служит параллелограмм.
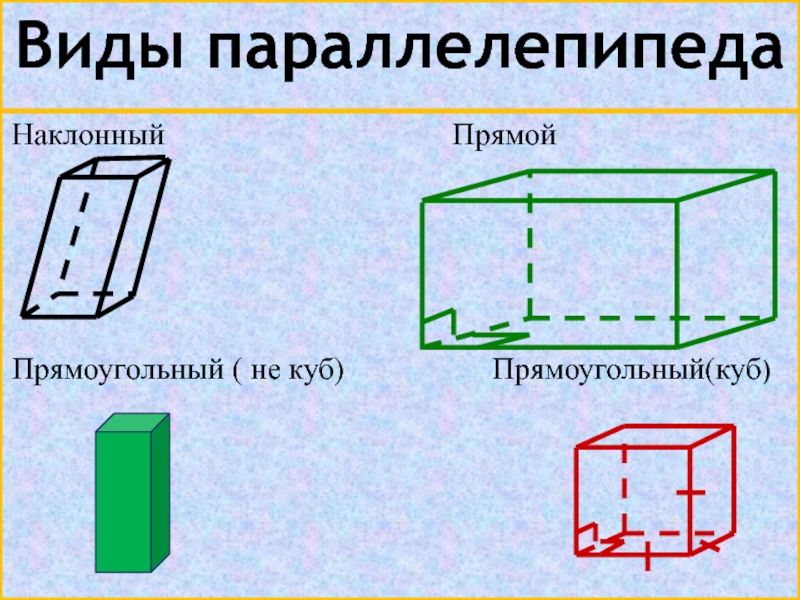
- 4. Виды параллелепипедаНаклонный
- 5. Прямой параллелепипед Параллелепипед называется прямым, если его
- 6. Прямоугольный параллелепипедПрямоугольным параллелепипедом называется прямой параллелепипед, основанием
- 7. Слайд 7
- 8. КубКубом называется прямоугольный параллелепипед, все ребра которого
- 9. Вычислительные формулы для кубаКвадрат диагонали куба равен утроенному квадрату его ребра:Площадь полной поверхности
- 10. Решение задач на нахождение элементов параллелепипедаЗадача №1Стороны
- 11. Задача №2Стороны основания прямого параллелепипеда 3
- 12. Решение задачПо данным чертежам найдите площадь боковой и полной поверхности параллелепипеда. Используйте справочный материал
- 13. Решение задачПо данным чертежам найдите площадь боковой и полной поверхности параллелепипеда. Используйте справочный материал
- 14. Задачи обязательного уровня по теме "Параллелепипед" 1.Измерения
- 15. 5.Одна из сторон основания прямоугольного параллелепипеда 4
- 16. 8. Основанием прямого параллелепипеда, высота которого равна
Название «параллелепипед» происходит от греческого слова «параллелос», означающего «параллельный», и греческого слова «эпипедос», означающего «плоскость», «поверхность». Слово встречалось у древнегреческих ученых Евклида и Герона.
Слайд 2Название «параллелепипед» происходит от греческого слова «параллелос», означающего «параллельный», и греческого
слова «эпипедос», означающего «плоскость», «поверхность». Слово встречалось у древнегреческих ученых Евклида и Герона.
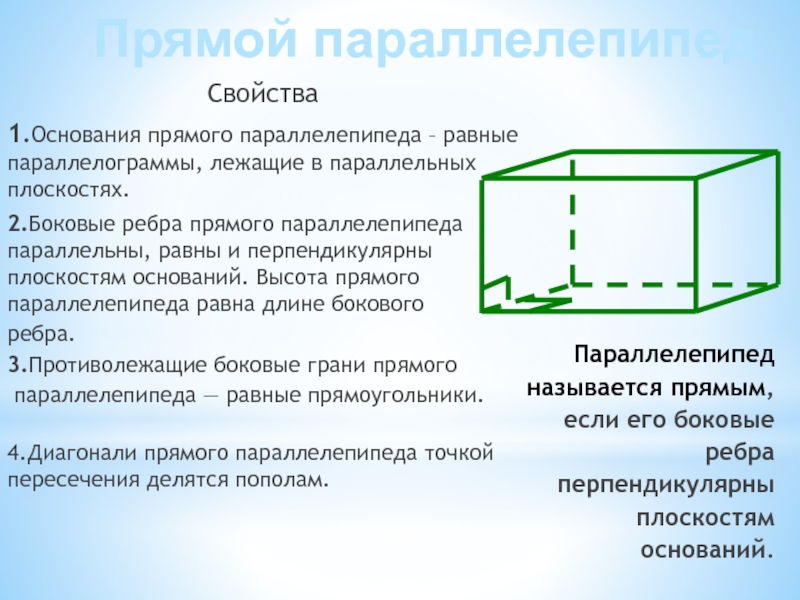
Слайд 5Прямой параллелепипед
Параллелепипед называется прямым, если его боковые ребра перпендикулярны плоскостям
оснований.
Свойства
1.Основания прямого параллелепипеда – равные параллелограммы, лежащие в параллельных плоскостях.
2.Боковые ребра прямого параллелепипеда параллельны, равны и перпендикулярны плоскостям оснований. Высота прямого параллелепипеда равна длине бокового
ребра.
3.Противолежащие боковые грани прямого
параллелепипеда — равные прямоугольники.
4.Диагонали прямого параллелепипеда точкой пересечения делятся пополам.
Слайд 6Прямоугольный параллелепипед
Прямоугольным параллелепипедом называется
прямой параллелепипед, основанием которого является прямоугольник.
Свойства
1.Противолежащие грани прямоугольного
параллелепипеда (в том числе основания) — равные прямоугольники.
2.Боковые ребра прямоугольного параллелепипеда параллельны, равны и перпендикулярны плоскостям оснований.
3.Все двугранные углы прямоугольного параллелепипеда - прямые.
4.Диагонали прямоугольного парал-
лелепипеда равны и точкой пересечения
делятся пополам.
5.Диагональные сечения
прямоугольного параллелепипеда - прямоугольники.
2.Боковые ребра прямоугольного параллелепипеда параллельны, равны и перпендикулярны плоскостям оснований.
3.Все двугранные углы прямоугольного параллелепипеда - прямые.
4.Диагонали прямоугольного парал-
лелепипеда равны и точкой пересечения
делятся пополам.
5.Диагональные сечения
прямоугольного параллелепипеда - прямоугольники.
Слайд 7
Вычислительные формулы для параллелепипеда
Прямоугольный параллелепипед
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов
трех его измерений:
Площадь боковой поверхности:
Площадь полной поверхности:
Площадь боковой поверхности:
Площадь полной поверхности:
Прямой параллелепипед
Площадь боковой поверхности:
Sб=Pосн · H
Площадь полной поверхности:
Sб=Pосн · H
Слайд 8Куб
Кубом называется прямоугольный параллелепипед,
все ребра которого равны.
Свойства куба
1.Все грани куба —
равные квадраты.
2.Из каждой вершины куба исходят три взаимно перпендикулярных равных ребра.
3.Все двугранные углы куба — прямые.
4.Диагонали куба с ребром а равны а√3 и точкой пересечения делятся пополам.
5.Диагональное сечение куба с ребром а — прямоугольник со сторонами а
и а√2 .
2.Из каждой вершины куба исходят три взаимно перпендикулярных равных ребра.
3.Все двугранные углы куба — прямые.
4.Диагонали куба с ребром а равны а√3 и точкой пересечения делятся пополам.
5.Диагональное сечение куба с ребром а — прямоугольник со сторонами а
и а√2 .
Слайд 9
Вычислительные формулы для куба
Квадрат диагонали куба равен утроенному квадрату его ребра:
Площадь
полной поверхности
Слайд 10Решение задач на нахождение элементов параллелепипеда
Задача №1
Стороны основания и диагональ прямоугольного
параллелепипеда равны соответственно 8 см, 9 см и 17 см. Найдите:
1)высоту параллелепипеда;
2)угол между диагональю параллелепипеда и плоскостью основания.
Дано
ABCDA1B1C1D1- параллелепипед,
AB=8 см,
AD=9 см,
B1D=17 см
Найти: 1) BB1=H; 2)
1)высоту параллелепипеда;
2)угол между диагональю параллелепипеда и плоскостью основания.
Дано
ABCDA1B1C1D1- параллелепипед,
AD=9 см,
B1D=17 см
Найти: 1) BB1=H; 2)
Слайд 11 Задача №2
Стороны основания прямого параллелепипеда 3 см и 5 см,
угол между ними 120 . Найдите:
1)боковое ребро и
2) меньшую диагональ параллелепипеда, если его большая диагональ 65 см.
Дано:
ABCDA1B1C1D1- параллелепипед AB=3 см, AD=5 см,Найти: AA1; B1D
Решение:
1)Большая диагональ прямого параллелепипеда проектируется в большую диагональ основания, AС>BD, следовательно, А1С - большая диагональ параллелепипеда.
1)боковое ребро и
2) меньшую диагональ параллелепипеда, если его большая диагональ 65 см.
Дано:
ABCDA1B1C1D1- параллелепипед AB=3 см, AD=5 см,
Решение:
1)Большая диагональ прямого параллелепипеда проектируется в большую диагональ основания, AС>BD, следовательно, А1С - большая диагональ параллелепипеда.
Слайд 12Решение задач
По данным чертежам найдите площадь боковой и полной поверхности параллелепипеда.
Используйте
справочный материал
справочный материал
Слайд 13Решение задач
По данным чертежам найдите площадь боковой и полной поверхности параллелепипеда.
Используйте
справочный материал
справочный материал
Слайд 14Задачи обязательного уровня по теме "Параллелепипед"
1.Измерения прямоугольного параллелепипеда 4 см, 6
см, 6 см. Вычислите площадь поверхности параллелепипеда.
2.Вычислите площадь поверхности куба, ребро которого 5 см.
3.Диагональ куба равна 10√3 см. Вычислите площадь поверхности куба.
4.Диагональ боковой грани прямого параллелепипеда равна 13 см а сторона квадрата, лежащего в основании, равна 5 см. Найдите площадь полной поверхности параллелепипеда.
2.Вычислите площадь поверхности куба, ребро которого 5 см.
3.Диагональ куба равна 10√3 см. Вычислите площадь поверхности куба.
4.Диагональ боковой грани прямого параллелепипеда равна 13 см а сторона квадрата, лежащего в основании, равна 5 см. Найдите площадь полной поверхности параллелепипеда.
Слайд 155.Одна из сторон основания прямоугольного параллелепипеда 4 см, а диагональ основания
равна 5 см. Вычислите площадь полной поверхности, если высота параллелепипеда равна
8 см.
6.В прямом параллелепипеде стороны основания 6см и 8 см образуют угол 30°, боковое ребро равно 10 см. Найдите полную поверхность параллелепи- педа.
7.В прямом параллелепипеде стороны основания 3 дм и 8 дм, угол между ними 60°. Боковая поверхность 220 дм2. Найдите полную поверхность параллелепипеда.
8 см.
6.В прямом параллелепипеде стороны основания 6см и 8 см образуют угол 30°, боковое ребро равно 10 см. Найдите полную поверхность параллелепи- педа.
7.В прямом параллелепипеде стороны основания 3 дм и 8 дм, угол между ними 60°. Боковая поверхность 220 дм2. Найдите полную поверхность параллелепипеда.
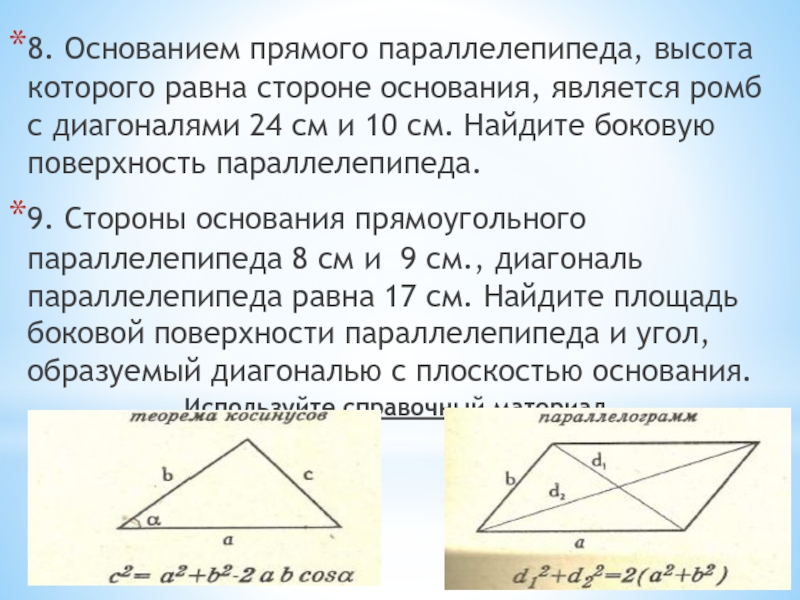
Слайд 168. Основанием прямого параллелепипеда, высота которого равна стороне основания, является ромб
с диагоналями 24 см и 10 см. Найдите боковую поверхность параллелепипеда.
9. Стороны основания прямоугольного параллелепипеда 8 см и 9 см., диагональ параллелепипеда равна 17 см. Найдите площадь боковой поверхности параллелепипеда и угол, образуемый диагональю с плоскостью основания.
Используйте справочный материал
9. Стороны основания прямоугольного параллелепипеда 8 см и 9 см., диагональ параллелепипеда равна 17 см. Найдите площадь боковой поверхности параллелепипеда и угол, образуемый диагональю с плоскостью основания.
Используйте справочный материал
