- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теме Теорема Пифагора
Содержание
- 1. Презентация к уроку по теме Теорема Пифагора
- 2. Детство и юностьГород ДельфахГермодамантЛесбос
- 3. Мать философа звали Партения (Партенида, Пифиада), а
- 4. Мистика и возвращение домойВавилонХалдеиПерсидские магиСтаринные легенды утверждают,
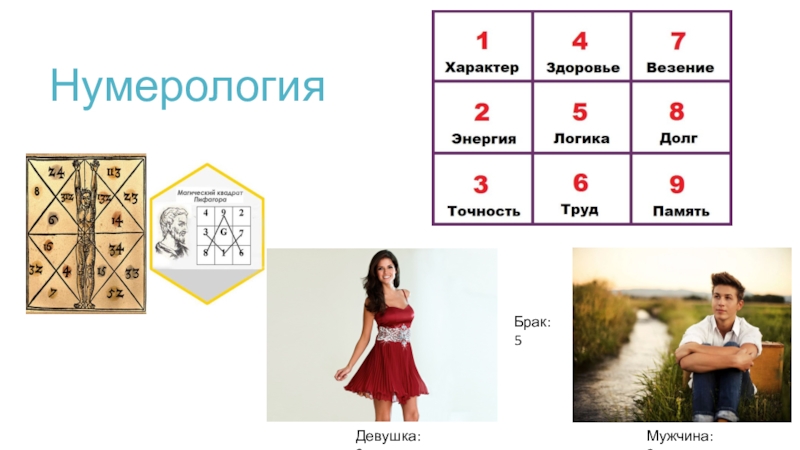
- 5. НумерологияДевушка:2Мужчина:3Брак:5
- 6. Философское учениеШкола ПифагораЗанятиеИзвестно, что Пифагор был религиозным
- 7. Город КротонГород МетапонтШкола в Метапонте
- 8. Использование теоремы Пифагора в повседневной жизниВ планиметрииВ стереометрииВ архитектуреВ физике
- 9. МатематикаПифагорВ прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузыТеорема Пифагора:acb
- 10. Доказательство 1Дано: ABC- равнобедренный, прямоугольный.Доказать:Для самого простого
- 11. Доказательство 2Дано: ABC- равнобедренный, прямоугольный.Доказать:Этот метод сочетает
- 12. Доказательство 3Дано: ABC- равнобедренный, прямоугольный.Доказать:Само же древнеиндийское
- 13. Доказательство 4Дано: ABC- равнобедренный, прямоугольный.Доказать:Это любопытное древнекитайское
- 14. Доказательство 5Дано: ABC- равнобедренный, прямоугольный.Доказать:Это еще один
- 15. Вывод:Теорема Пифагора действительно занимает важное место в
Детство и юностьГород ДельфахГермодамантЛесбос
Слайд 3Мать философа звали Партения (Партенида, Пифиада), а отца – Мнесарх. Согласно
легенде, однажды молодые супруги посетили город Дельфах в качестве свадебного путешествия. Там молодожены встретили оракула, который напророчил влюбленным скорое появление сына. Предание гласило, что ребенок станет непростым человеком, прославится мудростью, обликом, великими делами.
Вскоре пророчество начало сбываться, девушка родила мальчика и в соответствие с древней традицией получила имя Пифиада. Малыш назван Пифагором в честь жрицы Аполлона Пифии. Отец будущего математика старался всевозможными способами исполнить божественное предание. Счастливый Мнесарх воздвигает алтарь Аполлону, а ребенка окружает заботой и любовью.
Вскоре пророчество начало сбываться, девушка родила мальчика и в соответствие с древней традицией получила имя Пифиада. Малыш назван Пифагором в честь жрицы Аполлона Пифии. Отец будущего математика старался всевозможными способами исполнить божественное предание. Счастливый Мнесарх воздвигает алтарь Аполлону, а ребенка окружает заботой и любовью.
Пифагор
Слайд 4Мистика и возвращение домой
Вавилон
Халдеи
Персидские маги
Старинные легенды утверждают, что в Вавилоне талантливый
философ и божественной красоты человек (подтверждение тому - фото математика, сделанные на основе картин древних художников, скульптур) встретился с персидскими магами. Пифагор приобщился к изучению мистических событий, познал мудрость и особенности астрономии, арифметики, медицины восточных народов.
Слайд 6Философское учение
Школа Пифагора
Занятие
Известно, что Пифагор был религиозным новатором, создал тайное общество,
проповедовал акусматические положения. Он запрещал своим ученикам есть пищу животного происхождения, а особенно сердце, которое в первую очередь является символом жизни. Не разрешалось касаться бобов согласно легенде, полученных из крови Диониса-Загрея. Пифагором осуждалось употребление спиртного, сквернословие и прочее невежественное поведение.
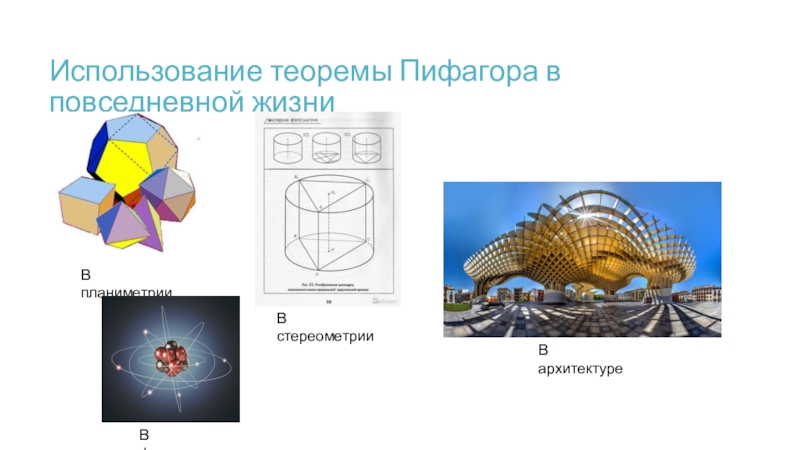
Слайд 8Использование теоремы Пифагора в повседневной жизни
В планиметрии
В стереометрии
В архитектуре
В физике
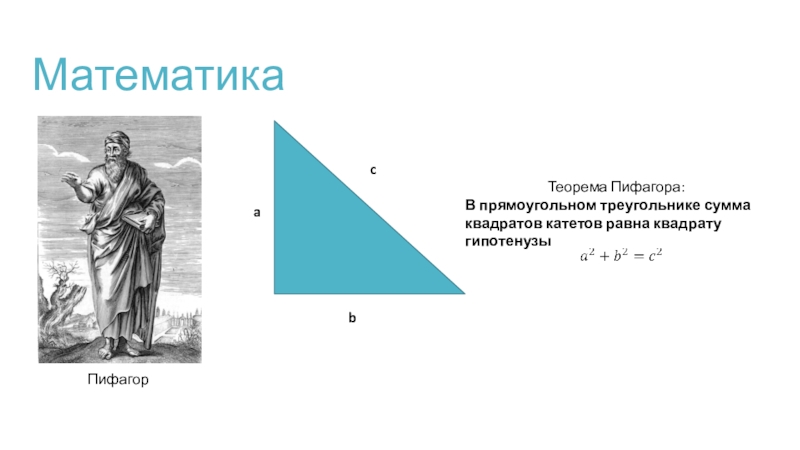
Слайд 9Математика
Пифагор
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы
Теорема Пифагора:
a
c
b
Слайд 10Доказательство 1
Дано:
ABC- равнобедренный, прямоугольный.
Доказать:
Для самого простого доказательства теоремы Пифагора для
прямоугольного треугольника нужно задать идеальные условия: пусть треугольник будет не только прямоугольным, но и равнобедренным. Есть основания полагать, что именно такой треугольник первоначально рассматривали математики древности.
Утверждение «квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах» можно проиллюстрировать следующим чертежом:
Доказательство теоремы Пифагора
Посмотрите на равнобедренный прямоугольный треугольник ABC: На гипотенузе АС можно построить квадрат, состоящий из четырех треугольников, равных исходному АВС. А на катетах АВ и ВС построено по квадрату, каждый из которых содержит по два аналогичных треугольника.
Кстати, этот чертеж лег в основу многочисленных анекдотов и карикатур, посвященных теореме Пифагора. Самый знаменитый, пожалуй, это «Пифагоровы штаны во все стороны равны»:
Утверждение «квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах» можно проиллюстрировать следующим чертежом:
Доказательство теоремы Пифагора
Посмотрите на равнобедренный прямоугольный треугольник ABC: На гипотенузе АС можно построить квадрат, состоящий из четырех треугольников, равных исходному АВС. А на катетах АВ и ВС построено по квадрату, каждый из которых содержит по два аналогичных треугольника.
Кстати, этот чертеж лег в основу многочисленных анекдотов и карикатур, посвященных теореме Пифагора. Самый знаменитый, пожалуй, это «Пифагоровы штаны во все стороны равны»:
Слайд 11Доказательство 2
Дано:
ABC- равнобедренный, прямоугольный.
Доказать:
Этот метод сочетает в себе алгебру и
геометрию и может рассматриваться как вариант древнеиндийского доказательства математика Бхаскари.
Постройте прямоугольный треугольник со сторонами a, b и c (рис.1). Затем постройте два квадрата со сторонами, равными сумме длин двух катетов, – (a+b). В каждом из квадратов выполните построения, как на рисунках 2 и 3.
В первом квадрате постройте четыре таких же треугольника, как на рисунке 1. В результате получаться два квадрата: один со стороной a, второй со стороной b.
Во втором квадрате четыре построенных аналогичных треугольника образуют квадрат со стороной, равной гипотенузе c.
Сумма площадей построенных квадратов на рис.2 равна площади построенного нами квадрата со стороной с на рис.3. Это легко проверить, высчитав площади квадратов на рис. 2 по формуле. А площадь вписанного квадрата на рисунке 3. путем вычитания площадей четырех равных между собой вписанных в квадрат прямоугольных треугольников из площади большого квадрата со стороной (a+b).
Записав все это, имеем: a2+b2=(a+b)2 – 2ab. Раскройте скобки, проведите все необходимые алгебраические вычисления и получите, что a2+b2= a2+b2. При этом площадь вписанного на рис.3. квадрата можно вычислить и по традиционной формуле S=c2. Т.е. a2+b2=c2 – вы доказали теорему Пифагора.
Постройте прямоугольный треугольник со сторонами a, b и c (рис.1). Затем постройте два квадрата со сторонами, равными сумме длин двух катетов, – (a+b). В каждом из квадратов выполните построения, как на рисунках 2 и 3.
В первом квадрате постройте четыре таких же треугольника, как на рисунке 1. В результате получаться два квадрата: один со стороной a, второй со стороной b.
Во втором квадрате четыре построенных аналогичных треугольника образуют квадрат со стороной, равной гипотенузе c.
Сумма площадей построенных квадратов на рис.2 равна площади построенного нами квадрата со стороной с на рис.3. Это легко проверить, высчитав площади квадратов на рис. 2 по формуле. А площадь вписанного квадрата на рисунке 3. путем вычитания площадей четырех равных между собой вписанных в квадрат прямоугольных треугольников из площади большого квадрата со стороной (a+b).
Записав все это, имеем: a2+b2=(a+b)2 – 2ab. Раскройте скобки, проведите все необходимые алгебраические вычисления и получите, что a2+b2= a2+b2. При этом площадь вписанного на рис.3. квадрата можно вычислить и по традиционной формуле S=c2. Т.е. a2+b2=c2 – вы доказали теорему Пифагора.
Слайд 12Доказательство 3
Дано:
ABC- равнобедренный, прямоугольный.
Доказать:
Само же древнеиндийское доказательство описано в XII
веке в трактате «Венец знания» («Сиддханта широмани») и в качестве главного аргумента автор использует призыв, обращенный к математическим талантам и наблюдательности учеников и последователей: «Смотри!».
Но мы разберем это доказательство более подробно:
Внутри квадрата постройте четыре прямоугольных треугольника так, как это обозначено на чертеже. Сторону большого квадрата, она же гипотенуза, обозначим с. Катеты треугольника назовем а и b. В соответствии с чертежом сторона внутреннего квадрата это (a-b).
Используйте формулу площади квадрата S=c2, чтобы вычислить площадь внешнего квадрата. И одновременно высчитайте ту же величину, сложив площадь внутреннего квадрата и площади всех четырех прямоугольных треугольников: (a-b)22+4*1\2*a*b.
Вы можете использовать оба варианта вычисления площади квадрата, чтобы убедиться: они дадут одинаковый результат. И это дает вам право записать, что c2=(a-b)2+4*1\2*a*b. В результате решения вы получите формулу теоремы Пифагора c2=a2+b2. Теорема доказана.
Но мы разберем это доказательство более подробно:
Внутри квадрата постройте четыре прямоугольных треугольника так, как это обозначено на чертеже. Сторону большого квадрата, она же гипотенуза, обозначим с. Катеты треугольника назовем а и b. В соответствии с чертежом сторона внутреннего квадрата это (a-b).
Используйте формулу площади квадрата S=c2, чтобы вычислить площадь внешнего квадрата. И одновременно высчитайте ту же величину, сложив площадь внутреннего квадрата и площади всех четырех прямоугольных треугольников: (a-b)22+4*1\2*a*b.
Вы можете использовать оба варианта вычисления площади квадрата, чтобы убедиться: они дадут одинаковый результат. И это дает вам право записать, что c2=(a-b)2+4*1\2*a*b. В результате решения вы получите формулу теоремы Пифагора c2=a2+b2. Теорема доказана.
Слайд 13Доказательство 4
Дано:
ABC- равнобедренный, прямоугольный.
Доказать:
Это любопытное древнекитайское доказательство получило название «Стул
невесты» - из-за похожей на стул фигуры, которая получается в результате всех построений:
В нем используется чертеж, который мы уже видели на рис.3 во втором доказательстве. А внутренний квадрат со стороной с построен так же, как в древнеиндийском доказательстве, приведенном выше.
Если мысленно отрезать от чертежа на рис.1 два зеленых прямоугольных треугольника, перенести их к противоположным сторонам квадрата со стороной с и гипотенузами приложить к гипотенузам сиреневых треугольников, получится фигура под названием «стул невесты» (рис.2). Для наглядности можно то же самое проделать с бумажными квадратами и треугольниками. Вы убедитесь, что «стул невесты» образуют два квадрата: маленькие со стороной b и большой со стороной a.
Эти построения позволили древнекитайским математикам и нам вслед за ними прийти к выводу, что c2=a2+b2.
В нем используется чертеж, который мы уже видели на рис.3 во втором доказательстве. А внутренний квадрат со стороной с построен так же, как в древнеиндийском доказательстве, приведенном выше.
Если мысленно отрезать от чертежа на рис.1 два зеленых прямоугольных треугольника, перенести их к противоположным сторонам квадрата со стороной с и гипотенузами приложить к гипотенузам сиреневых треугольников, получится фигура под названием «стул невесты» (рис.2). Для наглядности можно то же самое проделать с бумажными квадратами и треугольниками. Вы убедитесь, что «стул невесты» образуют два квадрата: маленькие со стороной b и большой со стороной a.
Эти построения позволили древнекитайским математикам и нам вслед за ними прийти к выводу, что c2=a2+b2.
Слайд 14Доказательство 5
Дано:
ABC- равнобедренный, прямоугольный.
Доказать:
Это еще один способ найти решение для
теоремы Пифагора, опираясь на геометрию. Называется он «Метод Гарфилда».
Постройте прямоугольный треугольник АВС. Нам надо доказать, что ВС2=АС2+АВ2.
Для этого продолжите катет АС и постройте отрезок CD, который равен катету АВ. Опустите перпендикулярный AD отрезок ED. Отрезки ED и АС равны. Соедините точки Е и В, а также Е и С и получите чертеж, как на рисунке ниже:
Доказательство теоремы Пифагора
Чтобы доказать терему, мы вновь прибегаем к уже опробованному нами способу: найдем площадь получившейся фигуры двумя способами и приравняем выражения друг к другу.
Найти площадь многоугольника ABED можно, сложив площади трех треугольников, которые ее образуют. Причем один из них, ЕСВ, является не только прямоугольным, но и равнобедренным. Не забываем также, что АВ=CD, АС=ED и ВС=СЕ – это позволит нам упростить запись и не перегружать ее. Итак, SABED=2*1/2(AB*AC)+1/2ВС2.
При этом очевидно, что ABED – это трапеция. Поэтому вычисляем ее площадь по формуле: SABED=(DE+AB)*1/2AD. Для наших вычислений удобней и наглядней представить отрезок AD как сумму отрезков АС и CD.
Запишем оба способа вычислить площадь фигуры, поставив между ними знак равенства: AB*AC+1/2BC2=(DE+AB)*1/2(AC+CD). Используем уже известное нам и описанное выше равенство отрезков, чтобы упростить правую часть записи: AB*AC+1/2BC2=1/2(АВ+АС)2. А теперь раскроем скобки и преобразуем равенство: AB*AC+1/2BC2=1/2АС2+2*1/2(АВ*АС)+1/2АВ2. Закончив все преобразования, получим именно то, что нам и надо: ВС2=АС2+АВ2. Мы доказали теорему.
Конечно, этот список доказательств далеко не полный. Теорему Пифагора также можно доказать с помощью векторов, комплексных чисел, дифференциальный уравнений, стереометрии и т.п. И даже физики: если, например, в аналогичные представленным на чертежах квадратные и треугольные объемы залить жидкость. Переливая жидкость, можно доказать равенство площадей и саму теорему в итоге.
Постройте прямоугольный треугольник АВС. Нам надо доказать, что ВС2=АС2+АВ2.
Для этого продолжите катет АС и постройте отрезок CD, который равен катету АВ. Опустите перпендикулярный AD отрезок ED. Отрезки ED и АС равны. Соедините точки Е и В, а также Е и С и получите чертеж, как на рисунке ниже:
Доказательство теоремы Пифагора
Чтобы доказать терему, мы вновь прибегаем к уже опробованному нами способу: найдем площадь получившейся фигуры двумя способами и приравняем выражения друг к другу.
Найти площадь многоугольника ABED можно, сложив площади трех треугольников, которые ее образуют. Причем один из них, ЕСВ, является не только прямоугольным, но и равнобедренным. Не забываем также, что АВ=CD, АС=ED и ВС=СЕ – это позволит нам упростить запись и не перегружать ее. Итак, SABED=2*1/2(AB*AC)+1/2ВС2.
При этом очевидно, что ABED – это трапеция. Поэтому вычисляем ее площадь по формуле: SABED=(DE+AB)*1/2AD. Для наших вычислений удобней и наглядней представить отрезок AD как сумму отрезков АС и CD.
Запишем оба способа вычислить площадь фигуры, поставив между ними знак равенства: AB*AC+1/2BC2=(DE+AB)*1/2(AC+CD). Используем уже известное нам и описанное выше равенство отрезков, чтобы упростить правую часть записи: AB*AC+1/2BC2=1/2(АВ+АС)2. А теперь раскроем скобки и преобразуем равенство: AB*AC+1/2BC2=1/2АС2+2*1/2(АВ*АС)+1/2АВ2. Закончив все преобразования, получим именно то, что нам и надо: ВС2=АС2+АВ2. Мы доказали теорему.
Конечно, этот список доказательств далеко не полный. Теорему Пифагора также можно доказать с помощью векторов, комплексных чисел, дифференциальный уравнений, стереометрии и т.п. И даже физики: если, например, в аналогичные представленным на чертежах квадратные и треугольные объемы залить жидкость. Переливая жидкость, можно доказать равенство площадей и саму теорему в итоге.
Слайд 15Вывод:
Теорема Пифагора действительно занимает важное место в математике, с ее помощью
можно вывести множество задач не только геометрических.
В своей работе я привел только не большой перечень информации о доказательстве теоремы. На самом деле различных видов доказательств этой теоремы намного больше.
В своей работе я привел только не большой перечень информации о доказательстве теоремы. На самом деле различных видов доказательств этой теоремы намного больше.