- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по дисциплине Математика на тему Объемы тел вращения
Содержание
- 1. Презентация к уроку по дисциплине Математика на тему Объемы тел вращения
- 2. Содержание. Понятие объема. Объём цилиндра.Объем конуса.Объем усеченного конуса.Объем шара и его частей.Решите задачу.
- 3. Понятие объема в пространстве вводится аналогично понятию
- 4. Объём цилиндраОбъём цилиндра равен произведению площади основания на высоту.
- 5. Объём цилиндра
- 6. Объем конуса. Объем конуса равен одной трети
- 7. Объем конуса
- 8. Объем усеченного конуса.Объем усеченного
- 9. Объем усеченного конуса.
- 10. Объем шара. Объем шара радиуса R равен:
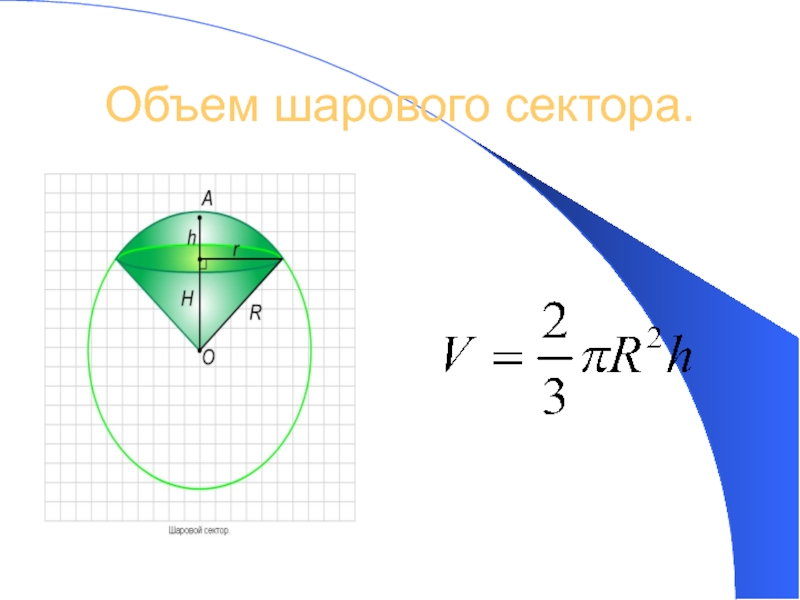
- 11. Объем шарового сектора.
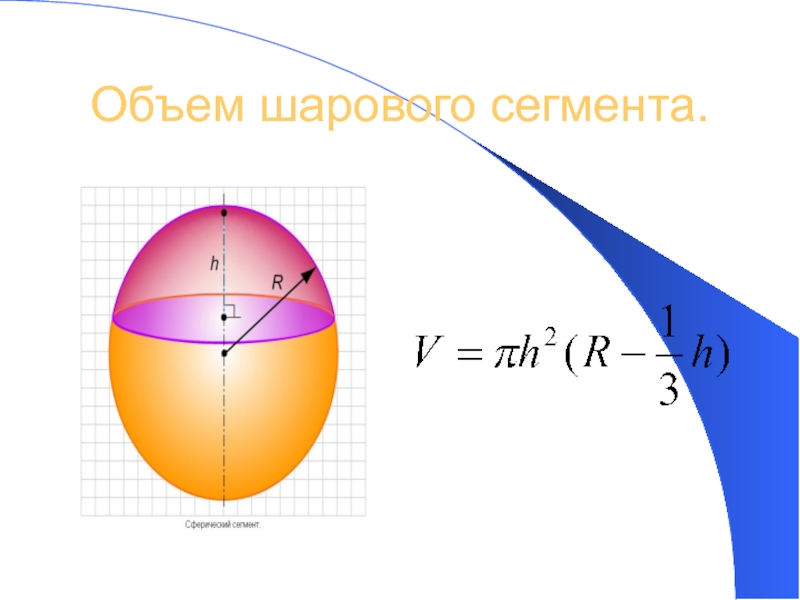
- 12. Объем шарового сегмента.
- 13. Объем шарового слоя.Объем шарового слоя можно вычислить как разность объемов двух шаровых сегментов.
- 14. V.Решите задачу.Задача 1. Объем цилиндра равен 16/
- 15. Источники информации:1. Рисунки и картинки взяты из
Содержание. Понятие объема. Объём цилиндра.Объем конуса.Объем усеченного конуса.Объем шара и его частей.Решите задачу.
Слайд 1
Презентация урока на тему:
Объемы тел вращения.
Автор работы:
преподаватель
математики
ГБПОУ РО «БКМТ»
Котелевская Е.А.
Слайд 2Содержание.
Понятие объема.
Объём цилиндра.
Объем конуса.
Объем усеченного конуса.
Объем шара и
его частей.
Решите задачу.
Слайд 3
Понятие объема в пространстве вводится аналогично понятию площади для фигур на
плоскости.
Определение 1. Объемом тела называется положительная величина, характеризующая часть пространства, занимаемую телом, и обладающая следующими свойствами:
равные тела имеют равные объемы; при параллельном переносе тела его объем не изменяется;
если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей;
за единицу объема принят объем куба, ребро которого равно единице длины;
Определение 2. Тела с равными объемами называются равновеликими. Из свойства 2 следует, что если тело с объемом V1 содержится внутри тела с объемом V2, то V1 < V2.
Определение 1. Объемом тела называется положительная величина, характеризующая часть пространства, занимаемую телом, и обладающая следующими свойствами:
равные тела имеют равные объемы; при параллельном переносе тела его объем не изменяется;
если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей;
за единицу объема принят объем куба, ребро которого равно единице длины;
Определение 2. Тела с равными объемами называются равновеликими. Из свойства 2 следует, что если тело с объемом V1 содержится внутри тела с объемом V2, то V1 < V2.
Понятие объема.
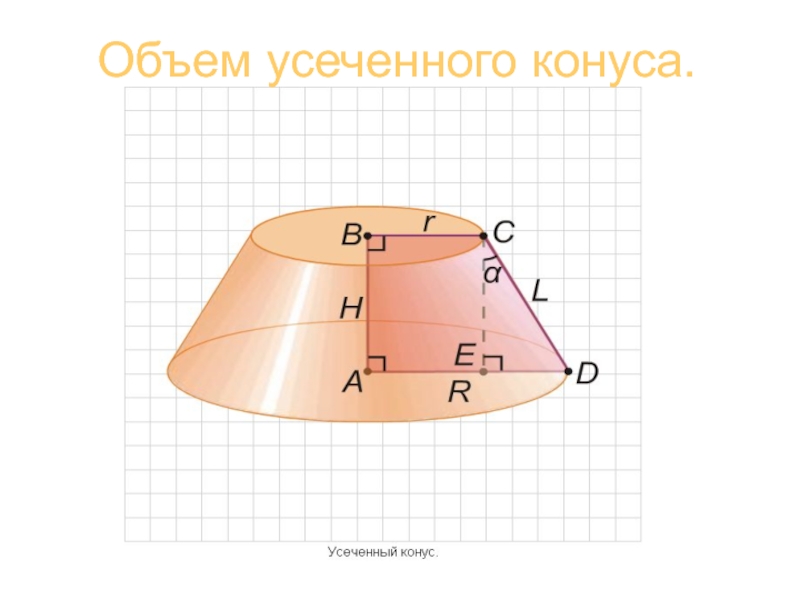
Слайд 8 Объем усеченного конуса.
Объем усеченного конуса равен:
где r
и R – радиусы оснований усеченного конуса.
Слайд 13Объем шарового слоя.
Объем шарового слоя можно вычислить как разность объемов двух
шаровых сегментов.
Слайд 14V.Решите задачу.
Задача 1. Объем цилиндра равен
16/ π. Боковая поверхность цилиндра
развертывается в квадрат. Определить сторону развертки.
Задача2. Площадь осевого сечения конуса 4,8 дм2. Высота конуса 3дм. Найти объем конуса.
Задача 3.Радиусы оснований усеченного конуса равны 3м и 6м, а образующая равна 5м.Вычислите объем усеченного конуса.
Задача 4. Диаметр шара разделен на три равные части и через точки деления проведены плоскости, перпендикулярные к диаметру.Найдите объем получившегося шарового слоя,если радиус шара равен R.
Задача2. Площадь осевого сечения конуса 4,8 дм2. Высота конуса 3дм. Найти объем конуса.
Задача 3.Радиусы оснований усеченного конуса равны 3м и 6м, а образующая равна 5м.Вычислите объем усеченного конуса.
Задача 4. Диаметр шара разделен на три равные части и через точки деления проведены плоскости, перпендикулярные к диаметру.Найдите объем получившегося шарового слоя,если радиус шара равен R.
Слайд 15Источники информации:
1. Рисунки и картинки взяты из Интернета и
диска
“Уроки геометрии Кирилла и
Мефодия”.
2. Формулы из учебника Геометрия 10-11 кл. сред. шк. Л.С.Атанасян и др.
3. Задачи из Сборника задач по элементарной математике для техникумов А.Е.Рудник.
Мефодия”.
2. Формулы из учебника Геометрия 10-11 кл. сред. шк. Л.С.Атанасян и др.
3. Задачи из Сборника задач по элементарной математике для техникумов А.Е.Рудник.