Разработан учителем математики Галиной Викторовной Ефремовой
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА (9 класс)
Содержание
- 1. Презентация к уроку геометрии ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА (9 класс)
- 2. Какие свойства площадей геометрических фигур иллюстрируют следующие
- 3. Проверка домашнего заданияРавновеликие фигуры1. «Перекроите» прямоугольник в
- 4. 2. «Перекроить» трапецию в параллелограмм.ВАСDABCD – параллелограмм,
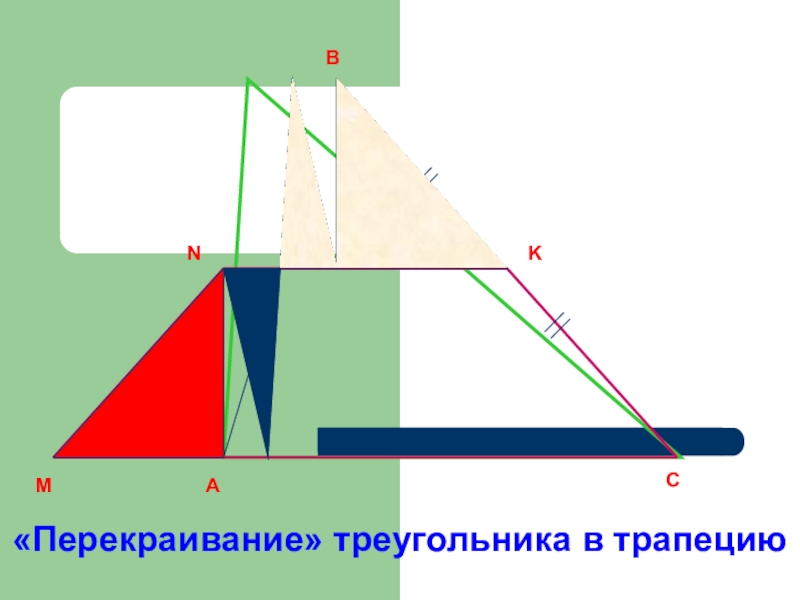
- 5. АВС«Перекраивание» треугольника в трапециюМNK
- 6. АТочки М, Р и К – середины сторон равностороннего ∆АВС? часть площади? часть площадиУстная работа1.
- 7. 2. Решите задачи:Стороны прямоугольника 2 см и
- 8. Тема урока:Площадь параллелограмма
- 9. KABCDHВопрос: как найти площадь параллелограмма?АВ = CD
- 10. Как же найти площадь параллелограмма?ABCDHAD – сторона
- 11. Вывод формулы площади параллелограмма.Теорема:Площадь параллелограмма равна произведению
- 12. Sпарал.=а·haSпарал.=b·hbУстно: 1) Найдите S, если а =
- 13. 1 вариант Стороны параллелограмма
- 14. АВСD150º10 cм6 cмВСD30º3 cм4 cмАКМНS = AD
- 15. Итоги урока1. Достигли мы поставленной цели?2. Какой
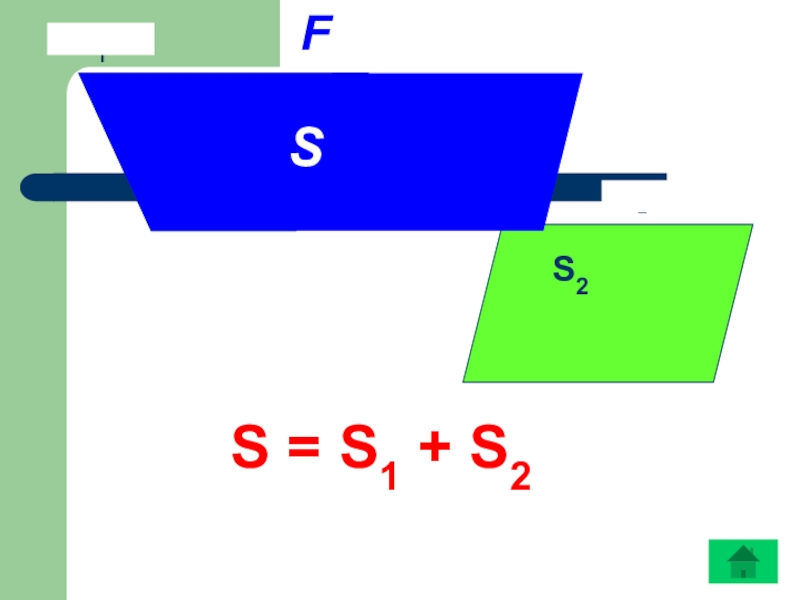
- 16. F1F2S1S2 SFS = S1 + S2
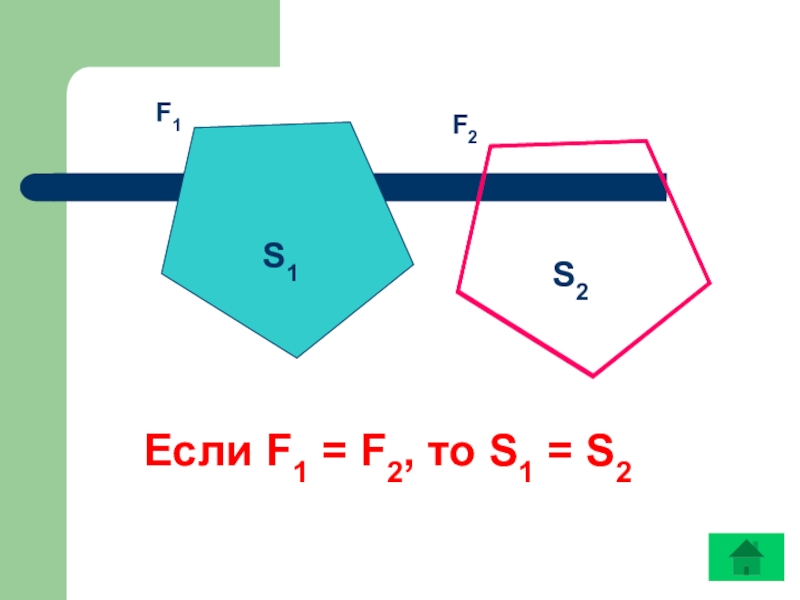
- 17. F2S1S2F1Если F1 = F2, то S1 = S2
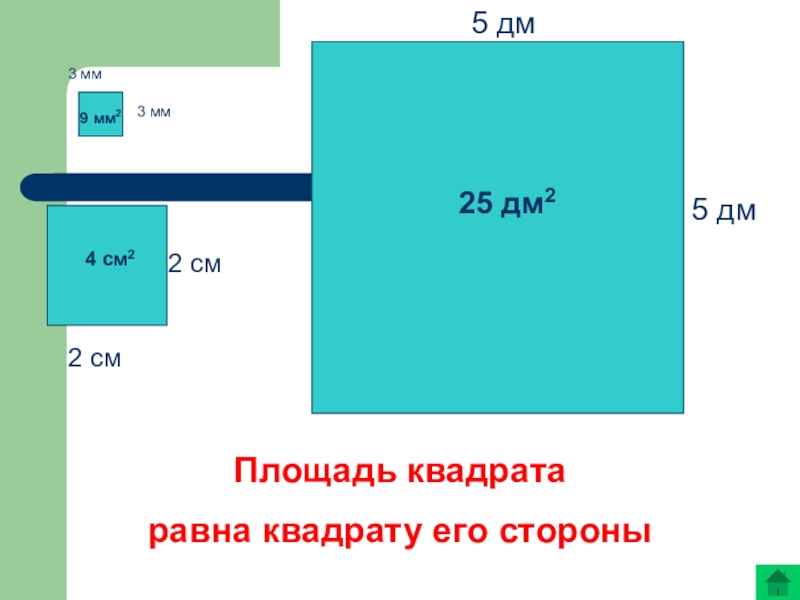
- 18. 3 мм3 мм2 см2 см5 дм5 дмПлощадь квадрата равна квадрату его стороны9 мм24 см225 дм2
- 19. До новых встреч
Какие свойства площадей геометрических фигур иллюстрируют следующие рисунки. Рисунок 1 Рисунок 2 Рисунок 32. Как вычислить площади квадрата и прямоугольника. Sкв = а2 Sпрям = abАктуализация знаний
Слайд 1МОБУ «Потанинская основная школа»
Урок геометрии
в 9 классе по теме
«Площадь
параллелограмма»
Слайд 2Какие свойства площадей геометрических фигур иллюстрируют следующие рисунки.
Рисунок
1
Рисунок 2
Рисунок 3
Рисунок 2
Рисунок 3
2. Как вычислить площади квадрата и прямоугольника.
Sкв = а2 Sпрям = ab
Актуализация знаний учащихся
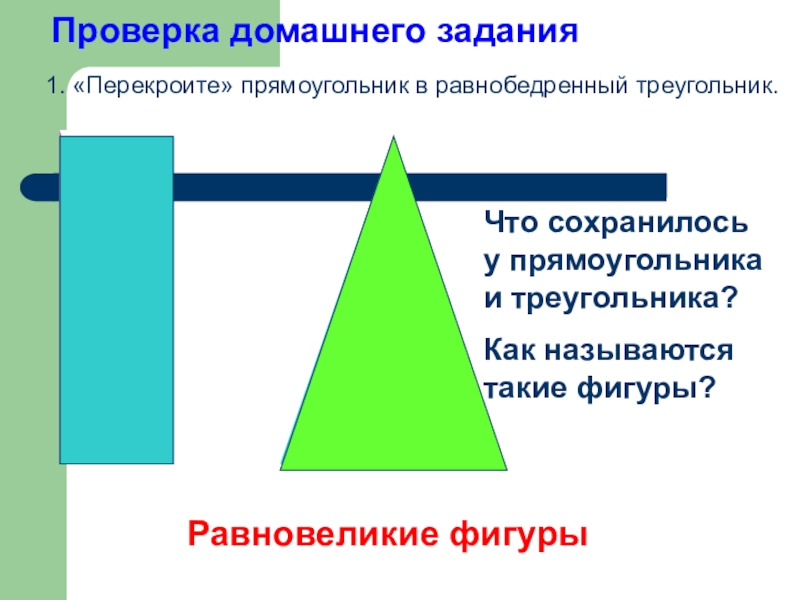
Слайд 3Проверка домашнего задания
Равновеликие фигуры
1. «Перекроите» прямоугольник в равнобедренный треугольник.
Что сохранилось у
прямоугольника и треугольника?
Как называются такие фигуры?
Как называются такие фигуры?
Слайд 4
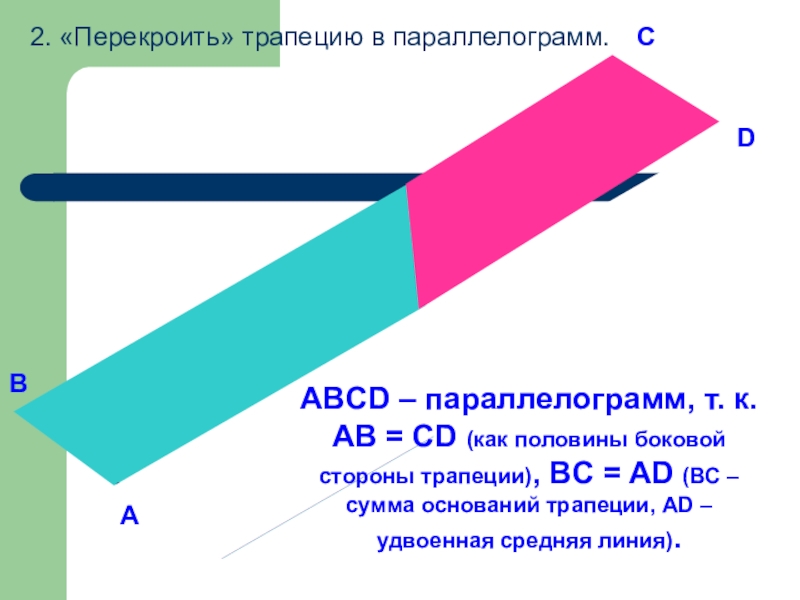
2. «Перекроить» трапецию в параллелограмм.
В
А
С
D
ABCD – параллелограмм, т. к. АВ =
СD (как половины боковой стороны трапеции), BC = AD (ВС – сумма оснований трапеции, АD – удвоенная средняя линия).
Слайд 6А
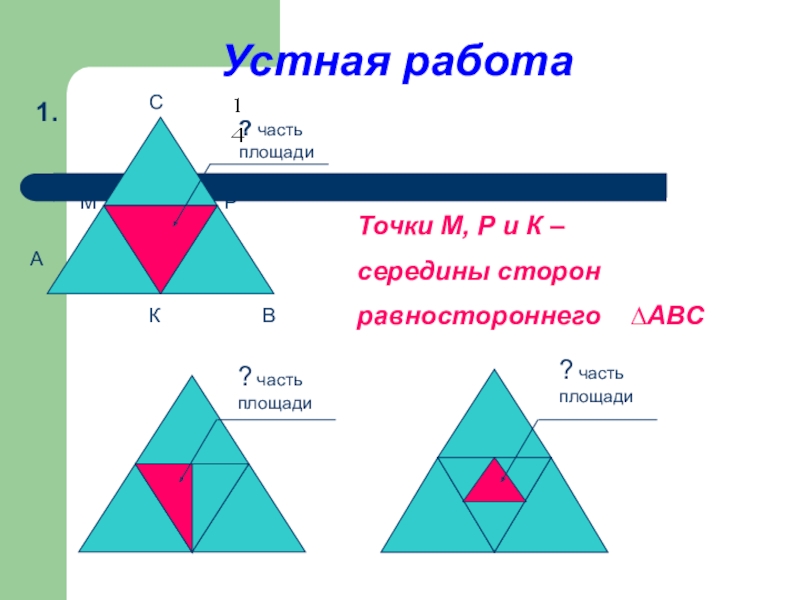
Точки М, Р и К –
середины сторон
равностороннего ∆АВС
?
часть площади
? часть площади
Устная работа
1.
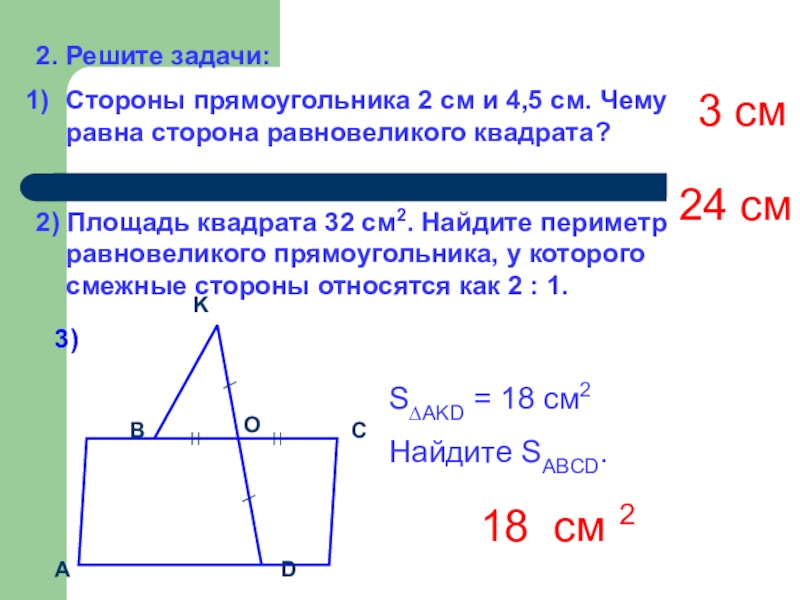
Слайд 72. Решите задачи:
Стороны прямоугольника 2 см и 4,5 см. Чему равна
сторона равновеликого квадрата?
2) Площадь квадрата 32 см2. Найдите периметр равновеликого прямоугольника, у которого смежные стороны относятся как 2 : 1.
2) Площадь квадрата 32 см2. Найдите периметр равновеликого прямоугольника, у которого смежные стороны относятся как 2 : 1.
А
В
С
D
K
O
S∆AKD = 18 см2
Найдите SABCD.
3)
3 см
24 см
18 см 2
Слайд 9K
A
B
C
D
H
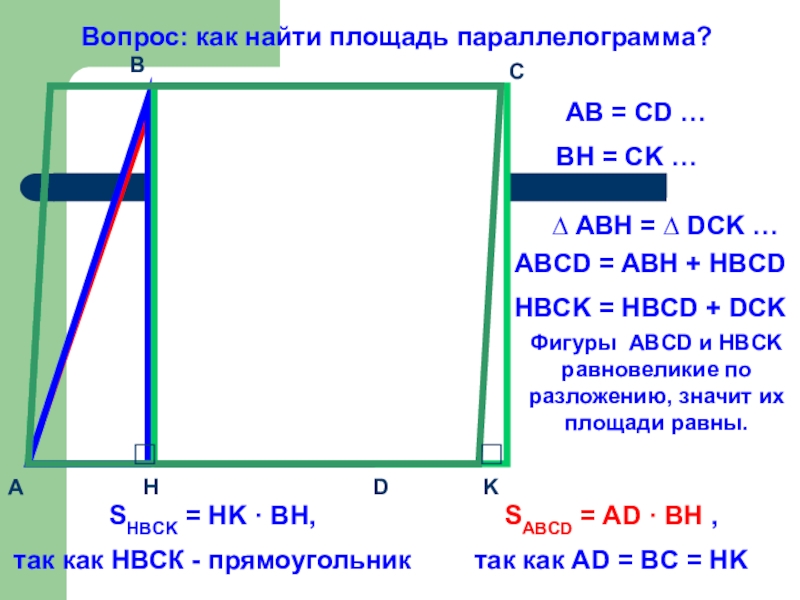
Вопрос: как найти площадь параллелограмма?
АВ = CD …
BH = CK …
∆ ABH = ∆ DCK …
ABCD = ABH + HBCD
HBCK = HBCD + DCK
Фигуры ABCD и HBCK равновеликие по разложению, значит их площади равны.
SABCD = AD · BH ,
так как AD = BC = HK
SHBCK = HK · BH,
так как НВСК - прямоугольник
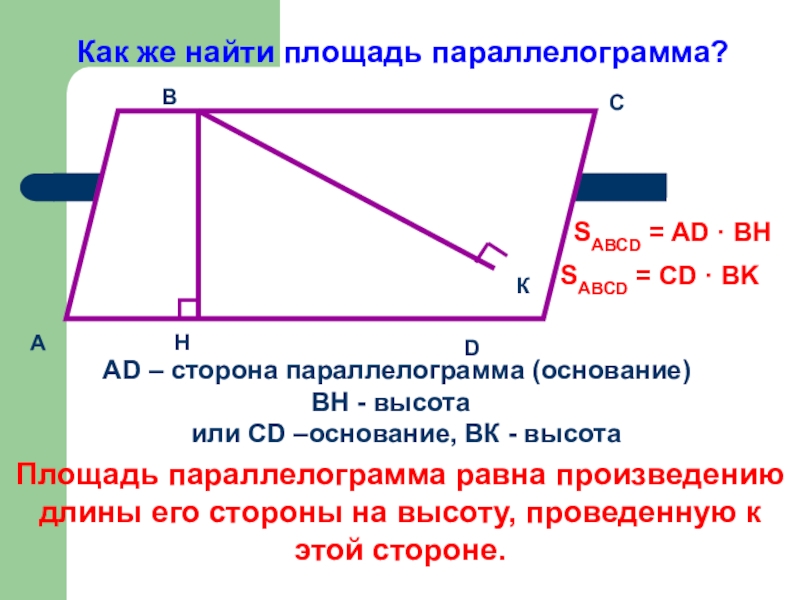
Слайд 10Как же найти площадь параллелограмма?
A
B
C
D
H
AD – сторона параллелограмма (основание)
ВН - высота
Площадь
параллелограмма равна произведению длины его стороны на высоту, проведенную к этой стороне.
К
или CD –основание, ВК - высота
SАВСD = AD · BH
SАВСD = CD · BK
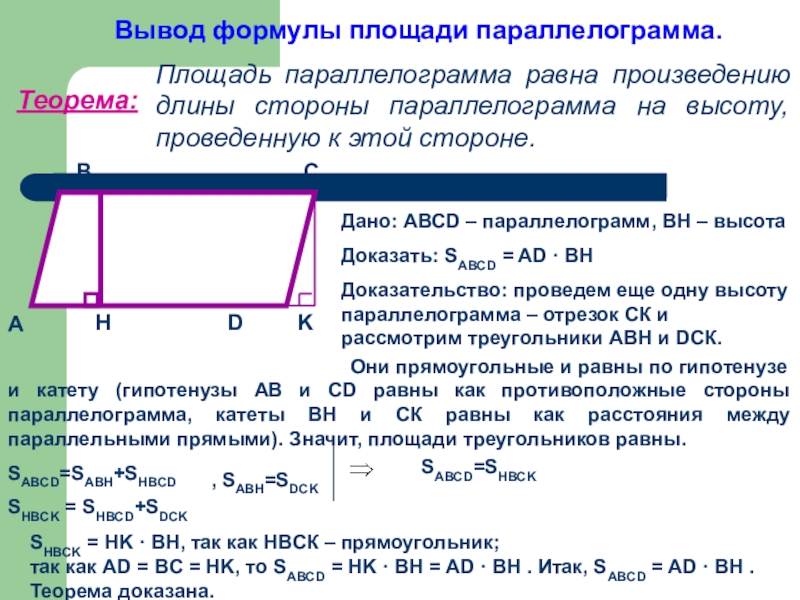
Слайд 11Вывод формулы площади параллелограмма.
Теорема:
Площадь параллелограмма равна произведению длины стороны параллелограмма на
высоту, проведенную к этой стороне.
A
B
C
D
H
Дано: АВСD – параллелограмм, ВН – высота
Доказать: SABCD = AD · BH
Доказательство: проведем еще одну высоту параллелограмма – отрезок СК и рассмотрим треугольники АВН и DСК.
K
Они прямоугольные и равны по гипотенузе и катету (гипотенузы АВ и СD равны как противоположные стороны параллелограмма, катеты ВН и СК равны как расстояния между параллельными прямыми). Значит, площади треугольников равны.
SABCD=SABH+SHBCD
SHBCK = SHBCD+SDCK
, SABH=SDCK
SABCD=SHBCK
SHBCK = HK · BH, так как НВСК – прямоугольник;
так как AD = BC = HK, то SABCD = HK · BH = AD · BH . Итак, SABCD = AD · BH .
Теорема доказана.
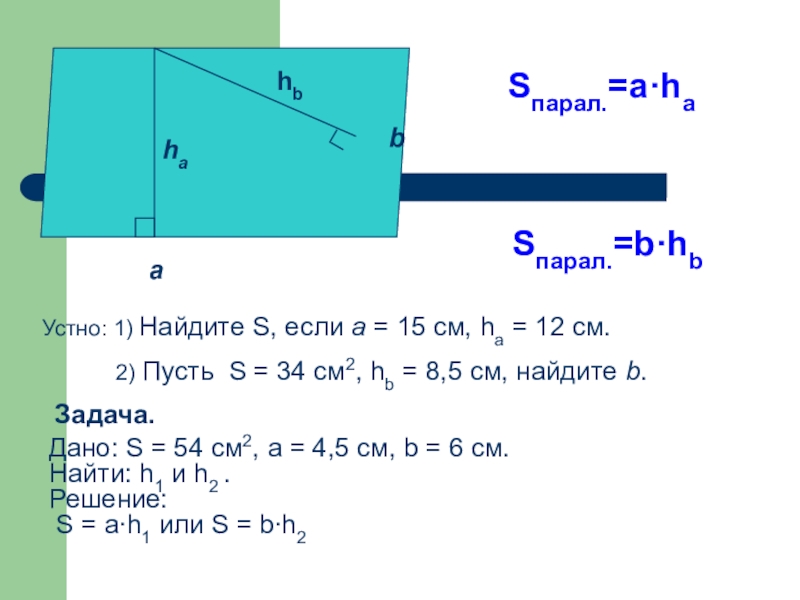
Слайд 12Sпарал.=а·ha
Sпарал.=b·hb
Устно: 1) Найдите S, если а = 15 см, ha =
12 см.
2) Пусть S = 34 см2, hb = 8,5 см, найдите b.
2) Пусть S = 34 см2, hb = 8,5 см, найдите b.
Задача.
Дано: S = 54 см2, а = 4,5 см, b = 6 cм.
Найти: h1 и h2 .
Решение:
S = a∙h1 или S = b∙h2
b
hb
Слайд 131 вариант
Стороны
параллелограмма
равны 10 см
и 6 см, а
угол между ними 150º.
Найдите
площадь этого
параллелограмма.
угол между ними 150º.
Найдите
площадь этого
параллелограмма.
2 вариант
Острый угол параллелограмма равен 30º, а высоты, проведенные из вершины тупого угла равны 4 см и 3 см.
Найдите
площадь этого параллелограмма.
Слайд 14
А
В
С
D
150º
10 cм
6 cм
В
С
D
30º
3 cм
4 cм
А
К
М
Н
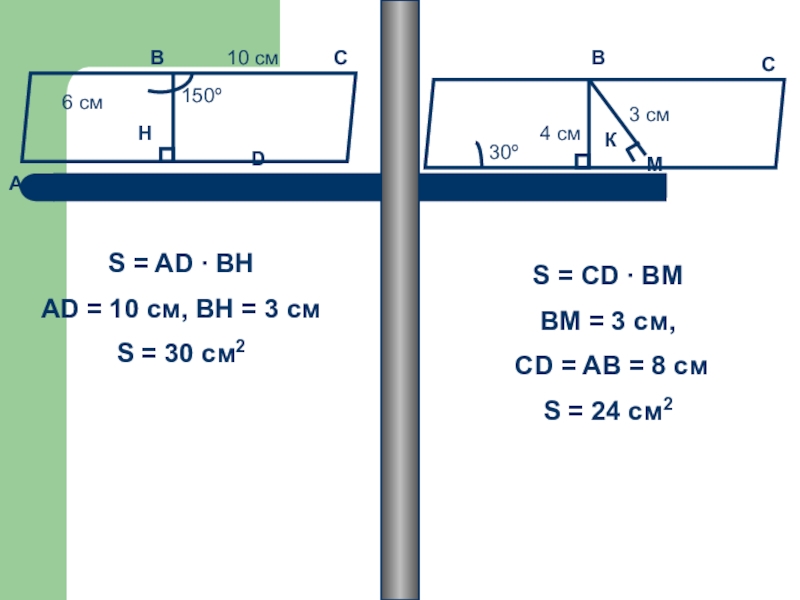
S = AD ∙ BH
AD = 10
cм, ВН = 3 см
S = 30 cм2
S = 30 cм2
S = CD ∙ BM
BM = 3 cм,
CD = AB = 8 cм
S = 24 cм2
Слайд 15Итоги урока
1. Достигли мы поставленной цели?
2. Какой главный итог нашего урока?
3.
Что мы использовали для достижения цели урока?
Домашнее задание:
п.123 стр. 184 теорема о площади параллелограмма,
№ 9, 11, 12 стр. 191
