- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии 8 класс на тему Теорема Пифагора
Содержание
- 1. Презентация к уроку геометрии 8 класс на тему Теорема Пифагора
- 2. Обобщить и систематизировать знания по темеЦель исследования:Если
- 3. Задачи исследования:Расширение познавательного интереса к изучению
- 4. Великий ученый Пифагор родился около 570г. до
- 5. Памятник Пифагору находится в порту города Пифагория
- 6. История теоремыИсторический обзор начнем с древнего Китая.
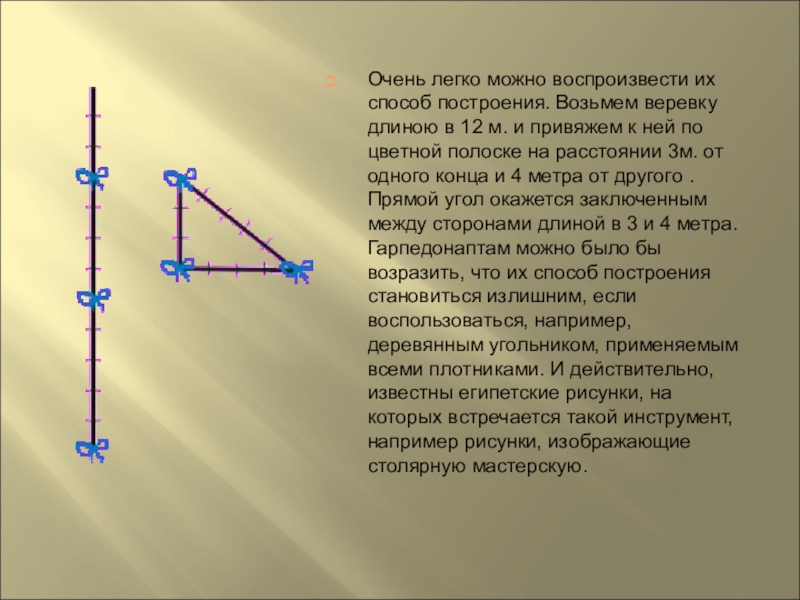
- 7. Очень легко можно воспроизвести их способ построения.
- 8. Этот способ применялся тысячелетия назад строителями египетских пирамид.СВ
- 9. Математические трактаты Древнего Китая дошли до нас
- 10. Заметим, что при таком доказательстве построения внутри
- 11. Несколько больше известно о теореме Пифагора у
- 12. "Заслугой первых греческих математиков, таких как Фалес,
- 13. Формулировки теоремыПриведем различные формулировки теоремы Пифагора в
- 14. В настоящее время известно, что эта теорема
- 15. В течение двух тысячелетий наиболее распространенным доказательством
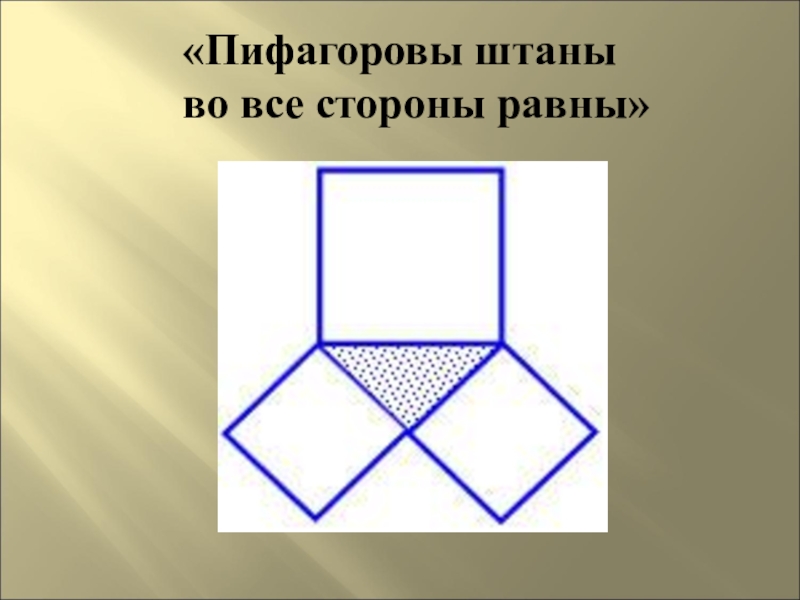
- 16. «Пифагоровы штаны во все стороны равны»
- 17. ПРОСТЕЙШИЕ ДОКАЗАТЕЛЬСТВАПростейшее доказательство теоремы получается в простейшем
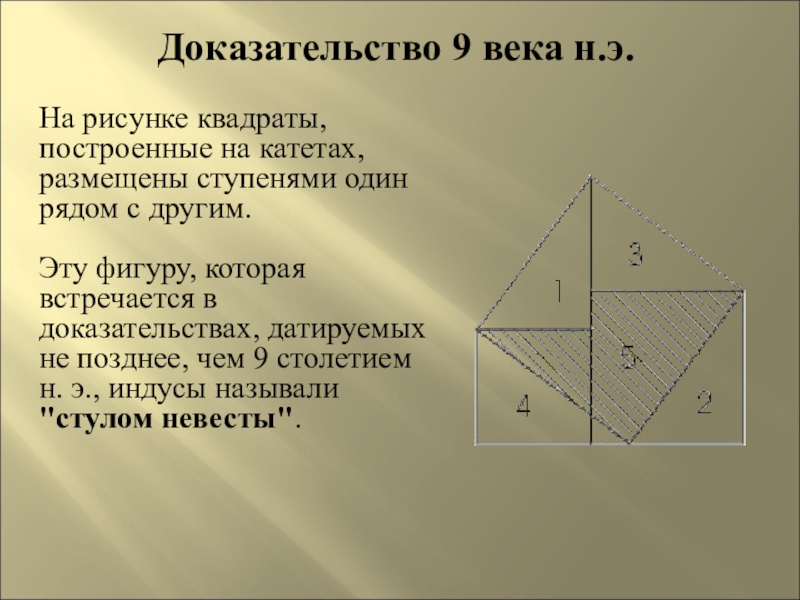
- 18. Доказательство 9 века н.э.На рисунке квадраты, построенные
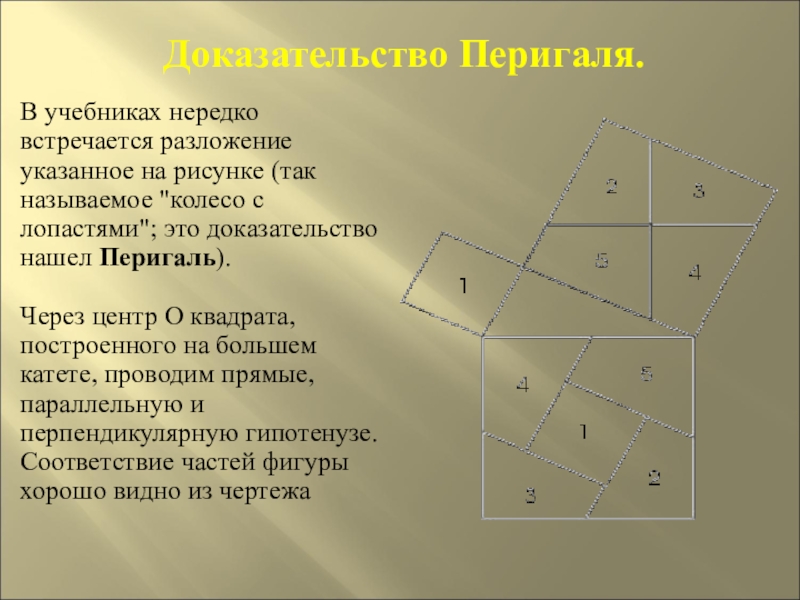
- 19. Доказательство Перигаля.В учебниках нередко встречается разложение указанное
- 20. Применение Теоремы ПифагораДиагональ d квадрата со стороной
- 21. Высота равностороннего треугольника Высота h равностороннего треугольника
- 22. Задача индийского математика XIIвека
- 23. Задача из учебника "Арифметика" Леонтия Магницкого«Случится
- 24. Слайд 24
- 25. В заключении еще раз хочется сказать о
- 26. ПОЛЕЗНЫЕ ССЫЛКИhttp://school-collection.edu.ru/catalog/rubr/7ae3b7e4-0a01-01b2-01d4-8209d17a43ff/54580/?interface=pupil&class=50&subject=18
- 27. СПАСИБО ЗА ВНИМАНИЕ
Слайд 1ТЕОРЕМА ПИФАГОРА
Автор работы - учитель математики
МБОУ Андреевская СОШ
Кунавина Вера Алексеевна
Слайд 2Обобщить и систематизировать знания по теме
Цель исследования:
Если дан нам треугольник,
И притом
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
И.Дырченко
Слайд 3 Задачи исследования:
Расширение познавательного интереса к изучению геометрии.
Разносторонний подход к изучению
Слайд 4
Великий ученый Пифагор родился около 570г. до н. э. на острове
По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.
Среди учителей юного Пифагора называетcя имена старца Гермодаманта и Ферекида Сиросского.
В Кротоне Пифагор учредил нечто вроде религиозно-этического братства, члены которого обязывались вести так называемый пифагорейский образ жизни.Это был одновременно и религиозный союз, и политический клуб, и научное общество.
…Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый , но злой, желает спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджегом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вкоре покончил жизнь самоубийством.
Биография Пифагора
Слайд 5Памятник Пифагору находится в порту города Пифагория и напоминает всем о
ПАМЯТЬ
Слайд 6История теоремы
Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает
"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Кантор (крупнейший немецкий историк математики) считает, что равенство
3 ² + 4 ² = 5²
было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).
По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Слайд 7Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в
Слайд 9 Математические трактаты Древнего Китая дошли до нас в редакции II в.
В IX книге "Математики" помещен чертеж, доказывающий теорему Пифагора (рис. ). Ключ к этому доказательству подобрать нетрудно. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а+b, а внутренний - квадрат со стороной с, построенный на гипотенузе
Слайд 10Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые
На последнем рисунке воспроизведен чертеж из трактата "Чжоу-би...". Здесь теорема Пифагора рассмотрена для египетского треугольника с катетами 3, 4 и гипотенузой 5 единиц измерения. Квадрат на гипотенузе содержит 25 клеток, а вписанный в него квадрат на большем катете - 16. Ясно, что оставшаяся часть содержит 9 клеток. Это и будет квадрат на меньшем катете.
Слайд 11Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте,
Слайд 12"Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является
Слайд 13Формулировки теоремы
Приведем различные формулировки теоремы Пифагора в переводе с греческого, латинского
У Евклида эта теорема гласит (дословный перевод):
"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".
В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так :
"Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".
В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так:
"В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".
Слайд 14В настоящее время известно, что эта теорема не была открыта Пифагором.
Например, что Пифагор в честь своего открытия принес в жертву богам 100 быков.
Слайд 15В течение двух тысячелетий наиболее распространенным доказательством теоремы Пифагора было придуманное
Евклид опускал высоту СН из вершины прямого угла на гипотенузу и доказывал, что её продолжение делит достроенный на гипотенузе квадрат на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах.
Чертёж, применяемый при доказательстве этой теоремы, в шутку называют «пифагоровы штаны». В течение долгого времени он считался одним из символов математической науки.
Слайд 17ПРОСТЕЙШИЕ ДОКАЗАТЕЛЬСТВА
Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника.
Слайд 18Доказательство 9 века н.э.
На рисунке квадраты, построенные на катетах, размещены ступенями
Эту фигуру, которая встречается в доказательствах, датируемых не позднее, чем 9 столетием н. э., индусы называли "стулом невесты".
Слайд 19Доказательство Перигаля.
В учебниках нередко встречается разложение указанное на рисунке (так называемое
Через центр O квадрата, построенного на большем катете, проводим прямые, параллельную и перпендикулярную гипотенузе. Соответствие частей фигуры хорошо видно из чертежа
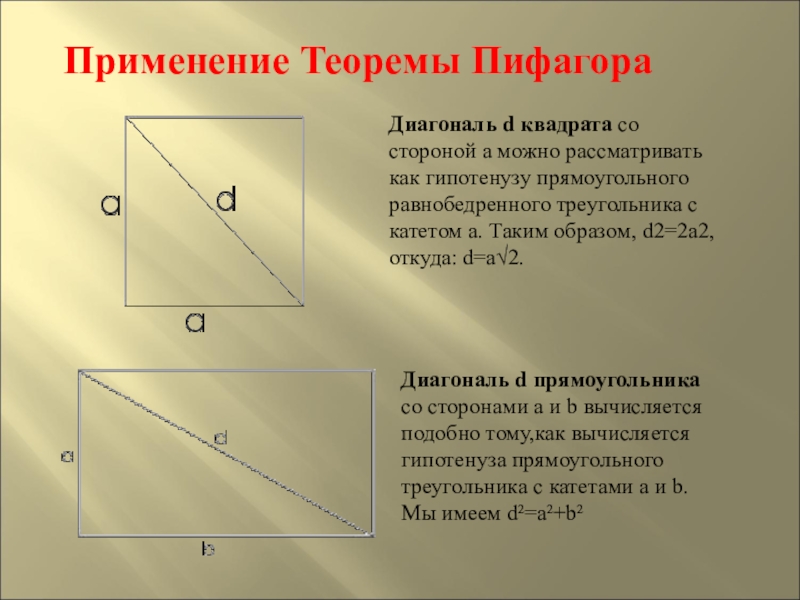
Слайд 20Применение Теоремы Пифагора
Диагональ d квадрата со стороной а можно рассматривать как
Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому,как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем d²=a²+b²
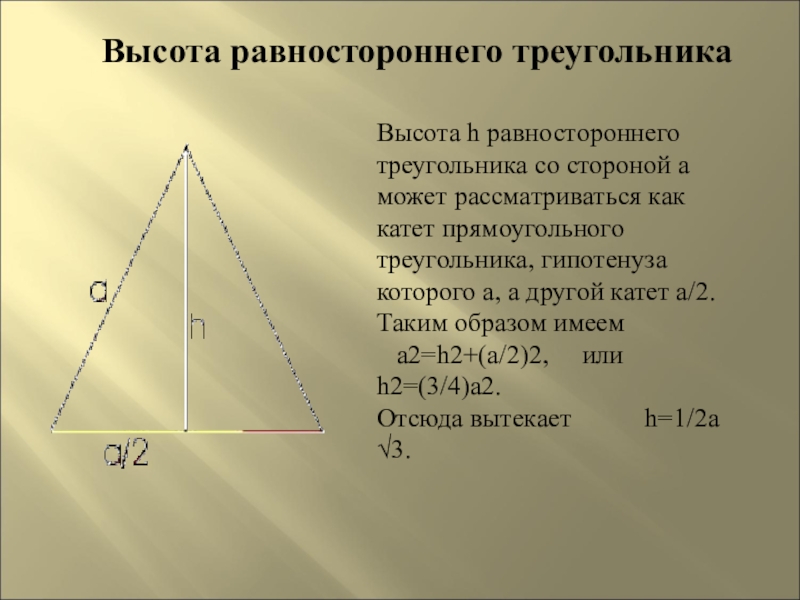
Слайд 21Высота равностороннего треугольника
Высота h равностороннего треугольника со стороной а может
a2=h2+(a/2)2, или h2=(3/4)a2.
Отсюда вытекает h=1/2а √3.
Слайд 22 Задача индийского математика XIIвека Бхаскары
"На берегу реки
Слайд 23 Задача из учебника "Арифметика" Леонтия Магницкого
«Случится некому человеку к стене
И обретете лестницу долготью 125 стоп.
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать»
Слайд 24 Задача из китайской "Математики
"Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его.
Спрашивается: какова глубина воды и какова длина камыша?"
Слайд 25В заключении еще раз хочется сказать о важности теоремы. Значение ее
Заключение
Суть истины вся в том, что нам она – навечно,
Когда хоть раз в прозрении её увидим свет,
И теорема Пифагора через столько лет
Для нас. Как для него, бесспорна, безупречна…
Отрывок из стихотворения А.Шамиссо
Слайд 26 ПОЛЕЗНЫЕ ССЫЛКИ
http://school-collection.edu.ru/catalog/rubr/7ae3b7e4-0a01-01b2-01d4-8209d17a43ff/54580/?interface=pupil&class=50&subject=18 - единая кол. Образ
http://school-collection.edu.ru/catalog/rubr/7ae3b7e4-0a01-01b2-01d4-8209d17a43ff/54581/?interface=pupil&class=50&subject=18 - Применение теоремы Пифагора
http://www.it-n.ru/board.aspx?cat_no=4510&tmpl=Thread&BoardId=4513&ThreadId=85690 - тест
http://www.edu-reforma.ru/load/2-1-0-723 -- разработка урока
http://www.it-n.ru/board.aspx?cat_no=4510&tmpl=Thread&BoardId=4513&ThreadId=85336 тренажер
http://multi-school.ucoz.ru/load/5-1-0-29- персональный сайт учителя
http://xn--www-qdd8aloyg.openclass.ru/dig-resource/39699 - открытый класс
http://rosedu.ru/detail_1185.html - Архив учебных программ