ДСОШ №4 с УИОП
г.Домодедово
Кириллина
Галина Александровна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Геометрия, 7 класс
Содержание
Задача №1. Из вершина прямого угла к гипотенузе прямоугольного треугольника проведена медиана. Найдите длину медианы, если длина гипотенузы равна 18 см.
Слайд 1
Самостоятельная работа по геометрии
с проверкой решения.
учитель математи
Учитель математики
МАОУ
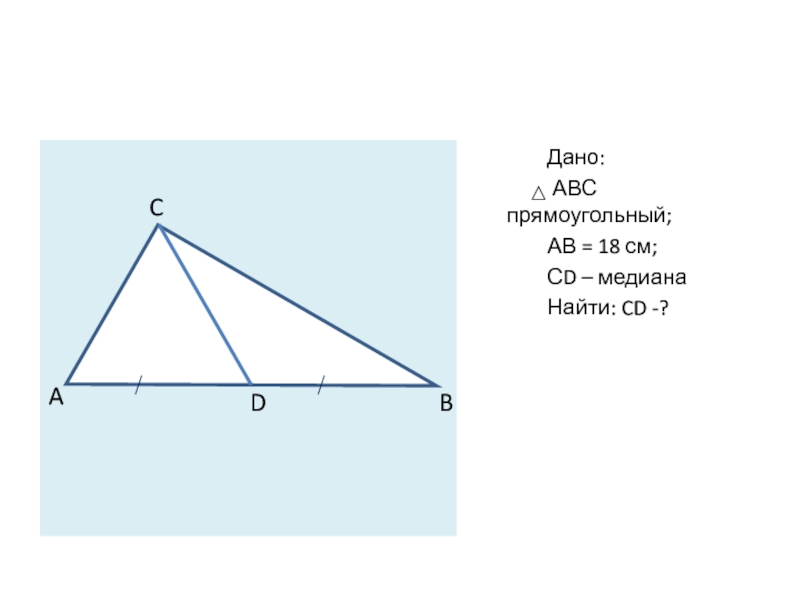
Слайд 2 Задача №1. Из вершина прямого угла к гипотенузе прямоугольного треугольника проведена
медиана. Найдите длину медианы, если длина гипотенузы равна 18 см.
Доказательная база:
Определение перпендикуляра.
Определение медианы треугольника.
Свойство параллельных прямых.
Признаки равенства прямоугольных треугольников.
Свойство медианы равнобедренного треугольника.
Определение равнобедренного треугольника.
Слайд 4Решение
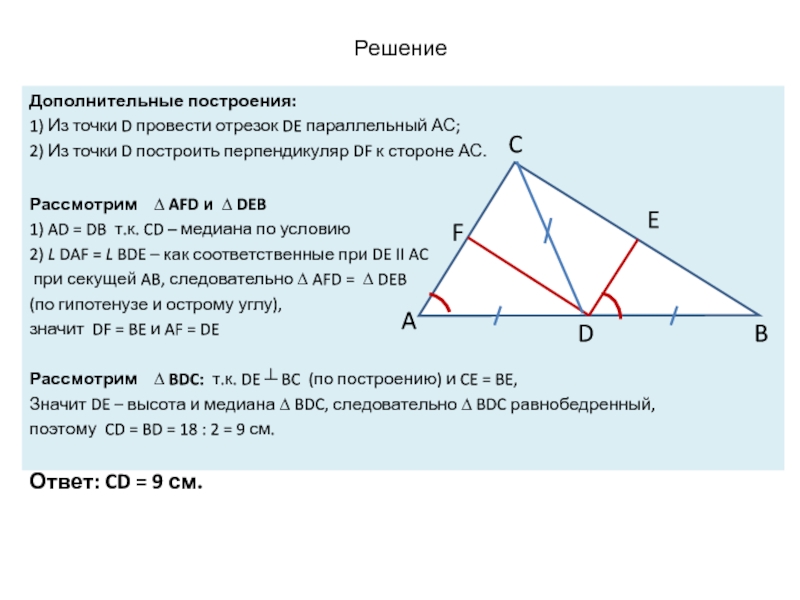
Дополнительные построения:
1) Из точки D провести отрезок DE параллельный АС;
2) Из
точки D построить перпендикуляр DF к стороне АС.
Рассмотрим ∆ AFD и ∆ DEB
1) AD = DB т.к. CD – медиана по условию
2) L DAF = L BDE – как соответственные при DE II AC
при секущей AB, следовательно ∆ AFD = ∆ DEB
(по гипотенузе и острому углу),
значит DF = BE и AF = DE
Рассмотрим ∆ BDC: т.к. DE ┴ BC (по построению) и CE = BE,
Значит DE – высота и медиана ∆ BDC, следовательно ∆ BDC равнобедренный,
поэтому CD = BD = 18 : 2 = 9 см.
Рассмотрим ∆ AFD и ∆ DEB
1) AD = DB т.к. CD – медиана по условию
2) L DAF = L BDE – как соответственные при DE II AC
при секущей AB, следовательно ∆ AFD = ∆ DEB
(по гипотенузе и острому углу),
значит DF = BE и AF = DE
Рассмотрим ∆ BDC: т.к. DE ┴ BC (по построению) и CE = BE,
Значит DE – высота и медиана ∆ BDC, следовательно ∆ BDC равнобедренный,
поэтому CD = BD = 18 : 2 = 9 см.
C
A
B
D
E
F
Ответ: CD = 9 см.
Слайд 5Задача №2. В равнобедренном треугольнике АВС к основанию АС проведена высота
ВН, равная 6 см, точка М – середина боковой стороны ВС. Найдите отрезок МН, если <АВС = 120˚
Доказательная база:
Определение равнобедренного треугольника.
Определение высоты треугольника.
Определение середины отрезка.
Определение медианы треугольника.
Теорема о биссектрисе равнобедренного треугольника, проведенной к основанию.
Теорема о сумме острых углов прямоугольного треугольника (1˚).
Свойство прямоугольных треугольников (2˚).
Слайд 6
Решение
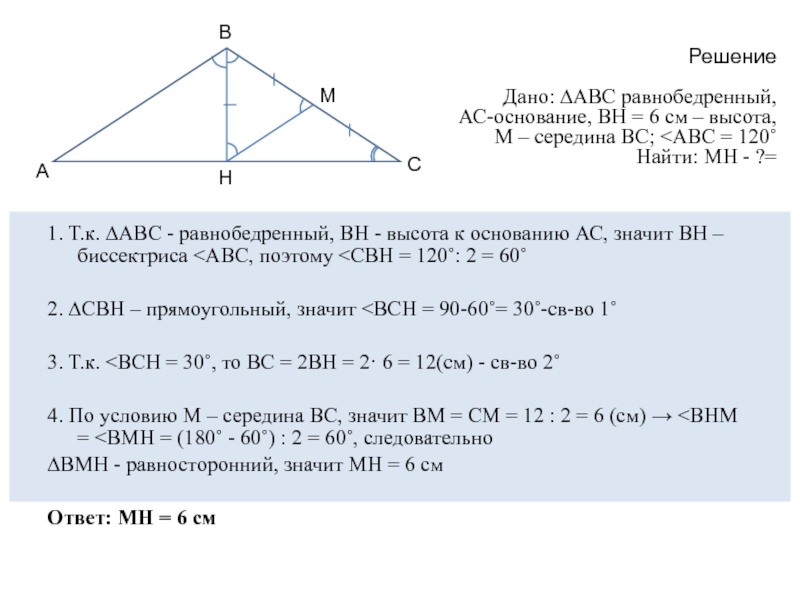
Дано: ∆АВС равнобедренный, АС-основание, ВН = 6 см – высота, М – середина ВС; <АВС = 120˚ Найти: МН - ?=
1. Т.к. ∆АВС - равнобедренный, ВН - высота к основанию АС, значит ВН – биссектриса <АВС, поэтому <СВН = 120˚: 2 = 60˚
2. ∆СВН – прямоугольный, значит <ВСН = 90-60˚= 30˚-св-во 1˚
3. Т.к. <ВСН = 30˚, то ВС = 2ВН = 2· 6 = 12(см) - св-во 2˚
4. По условию М – середина ВС, значит ВМ = СМ = 12 : 2 = 6 (см) → <ВНМ = <ВМН = (180˚ - 60˚) : 2 = 60˚, следовательно
∆ВМН - равносторонний, значит МН = 6 см
Ответ: МН = 6 см
A
B
H
C
M
