- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Построение сечений многогранников
Содержание
- 1. Построение сечений многогранников
- 2. «Скажи мне – и я забуду.
- 3. Многие художники,
- 4. МНОГОГРАННИК Многогранник - геометрическое тело, ограниченное со
- 5. Мы привыкли видеть как нарезаются продукты питания , а как будет выглядеть многогранник в разрезе ?
- 6. Вопросы, которые надо обсудитьЧто такое многогранник?Какой многогранник
- 7. Цели урока: Формирование у учащихся навыков решения
- 8. Взаимное расположение плоскости и многогранникаВАНет точек пересеченияОдна точка пересеченияПересечением является отрезокПересечением является плоскость
- 9. Слайд 9
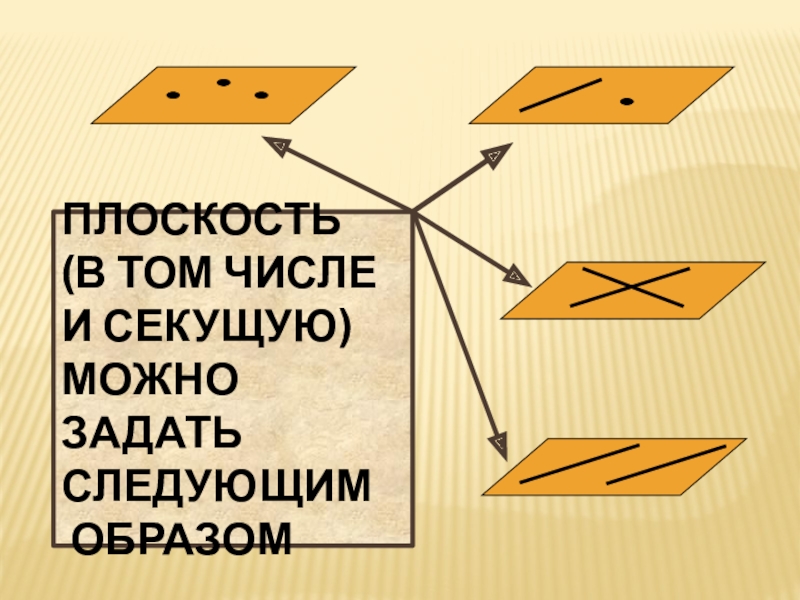
- 10. Плоскость (в том числе и секущую) можно задать следующим образом
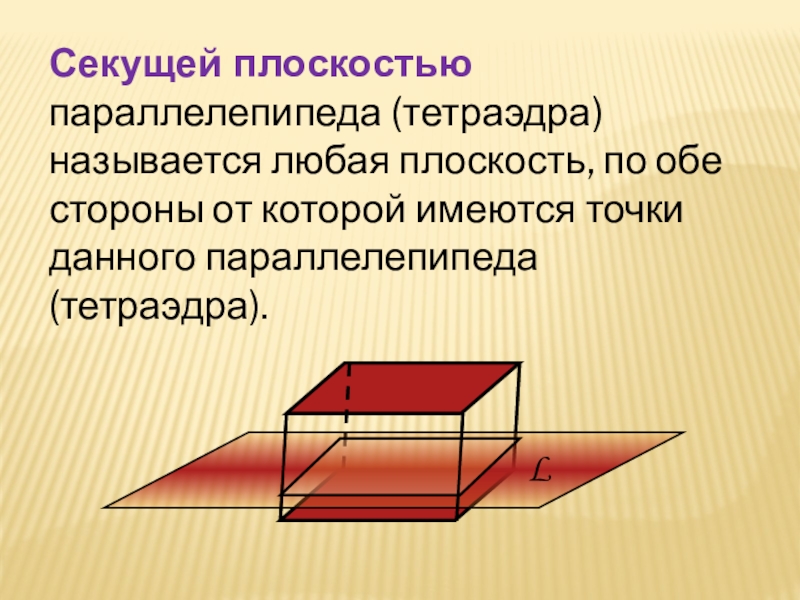
- 11. Секущей плоскостью параллелепипеда (тетраэдра) называется любая плоскость,
- 12. Построить сечение многогранника плоскостью –
- 13. Секущая плоскостьсечениеСекущая плоскость пересекает грани тетраэдра по
- 14. При этом необходимо учитывать следующее:1. Соединять можно
- 15. Какие многоугольники могут получиться в сечении ?Тетраэдр имеет 4 граниВ сечениях могут получиться:ЧетырехугольникиТреугольники
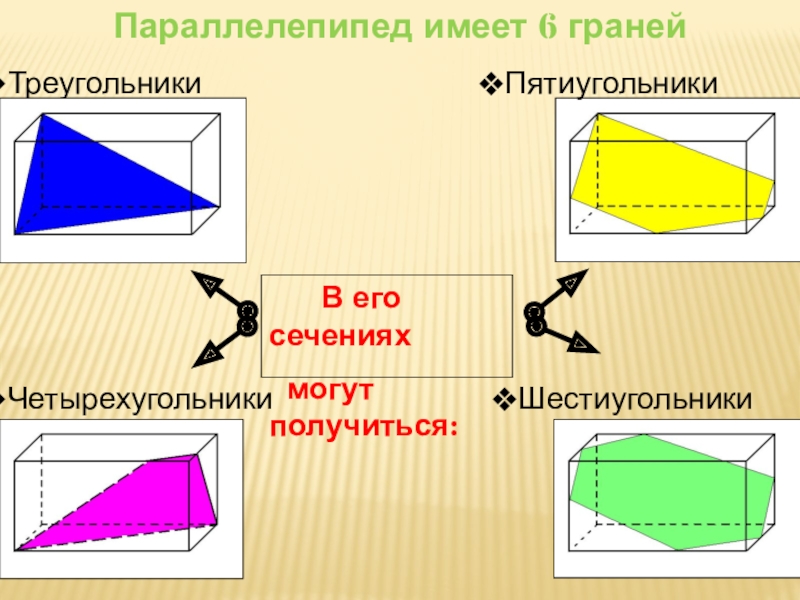
- 16. ТреугольникиПараллелепипед имеет 6 гранейЧетырехугольники ШестиугольникиПятиугольники В его сечениях могут получиться:
- 17. Блиц - опросЗадача блиц – опроса: ответить
- 18. АКСИОМЫпланиметриястереометрия1. Каждой прямой принадлежат по крайней мере
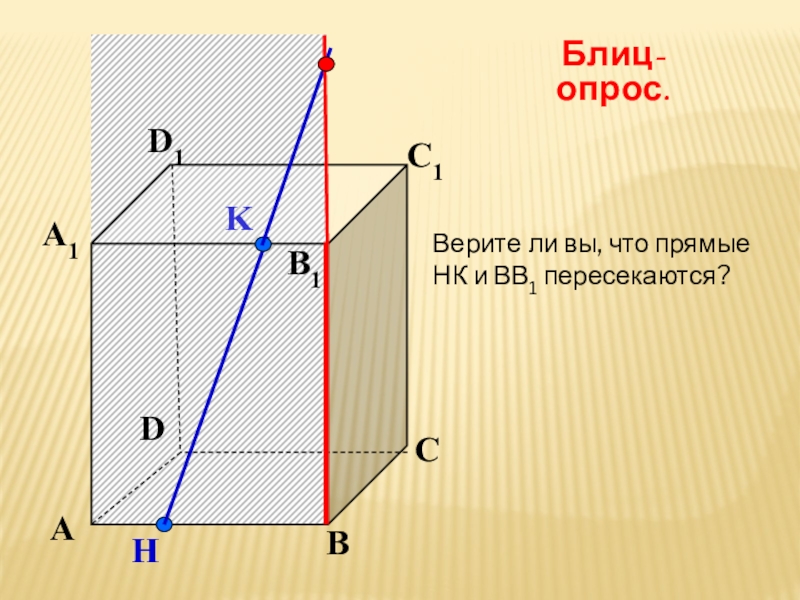
- 19. KАВСDА1D1С1B1HБлиц-опрос.Верите ли вы, что прямые НК и ВВ1 пересекаются?
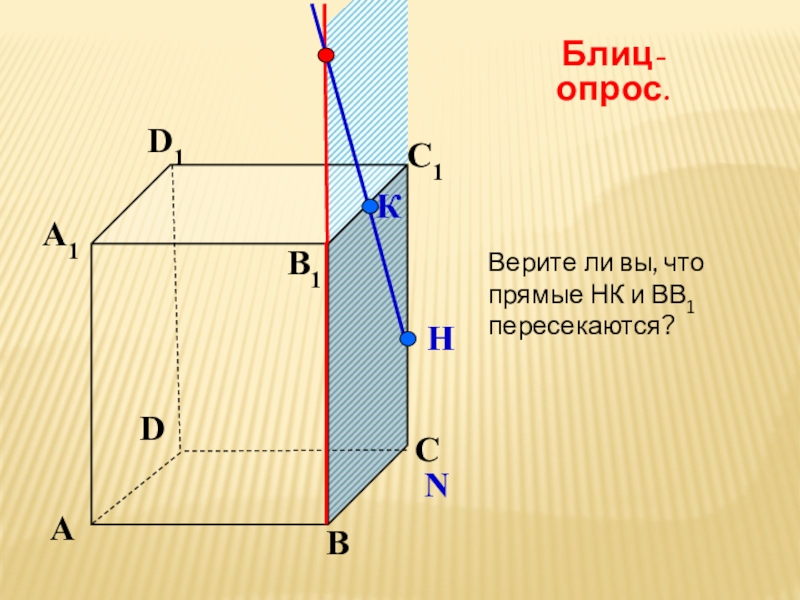
- 20. АВСDА1D1С1B1NКНБлиц-опрос. Верите ли вы,
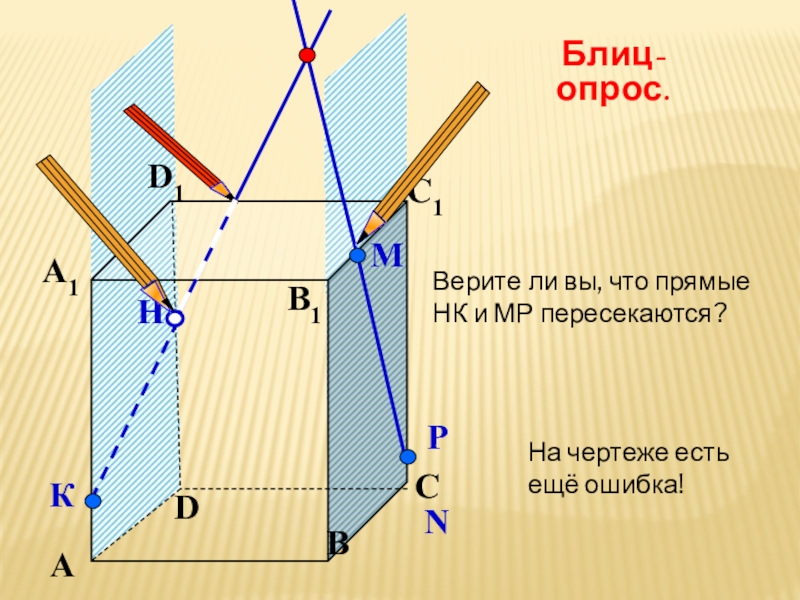
- 21. АВСDА1D1С1B1Верите ли вы, что прямые НК и МР пересекаются? NРНКМБлиц-опрос.На чертеже есть ещё ошибка!
- 22. АВСDА1D1С1B1Пересекаются ли прямые НR и А1В1? NНКБлиц-опрос.RПересекаются
- 23. Умение решать задачи – практическое искусство, подобное
- 24. Если две параллельные плоскости
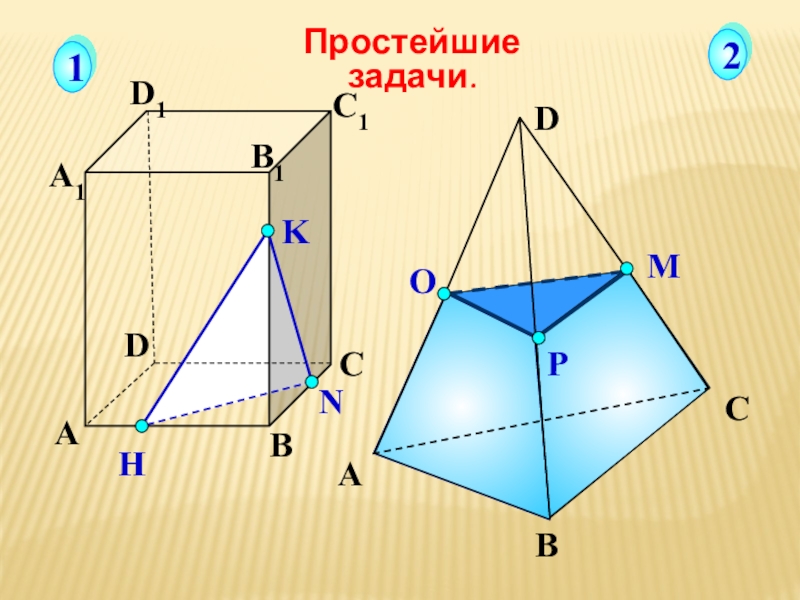
- 25. АВСDА1D1С1B1NHKПростейшие задачи.12
- 26. АВСDА1D1С1B1Диагональные сечения.56
- 27. АВСDА1D1С1B1NHО7K
- 28. Аксиоматический метод
- 29. ABCDKLMNFG Проводим через точки F и O
- 30. ABCDKLMNFG Шаг 2: ищем след секущей плоскости
- 31. ABCDKLMNFGШаг 3: делаем разрезы на других
- 32. CBADKLMNFGШаг 4: выделяем сечение многогранника Все разрезы
- 33. Самостоятельная работа.(с последующей проверкой)
- 34. PNMNPMNPMРешения варианта 1.Решения варианта 2.MNPMNPMNP
- 35. Правила для самоконтроля:Вершины сечения находятся только на
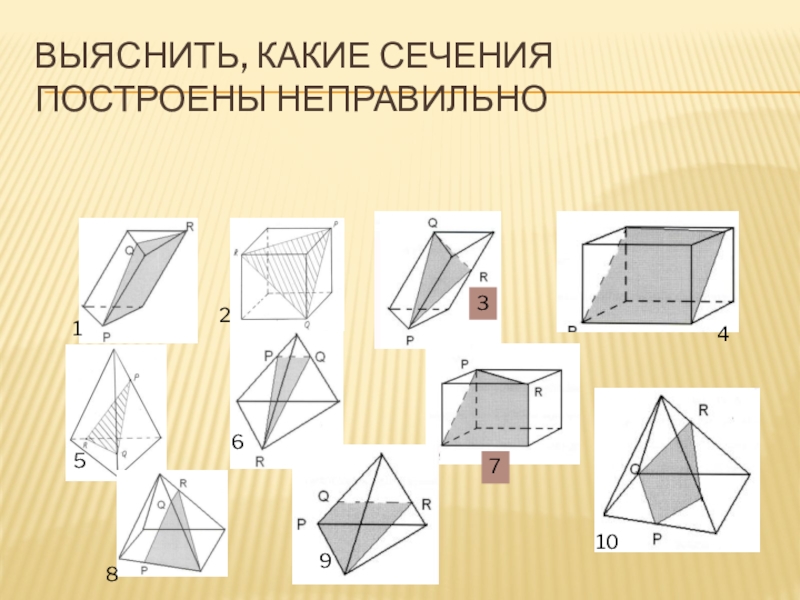
- 36. Выяснить, какие сечения построены неправильно12345687910
- 37. КроссвордБесконечная ровная поверхностьСторона грани многогранника.Основное понятие геометрии
- 38. Составить две задачи на
- 39. Слайд 39
- 40. Если вы хотите научиться плавать, то смело
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
Слайд 2«Скажи мне – и я забуду. Покажи мне – и я
Древняя китайская
пословица
Слайд 3
Многие художники, искажая законы перспективы, рисуют
Популярные художники Морис Эшер, Оскар Реутерсвард, Жос де Мей и другие, удивляли своими картинами математиков.
http://lib.world-mobile.net/culture/special/imp/imp-world-r.narod.ru/art/index.html
http://www.im-possible.info/english/art/mey/mey2.html
http://alone.sammit.kiev.ua/moremind/illusion/index.html
Это интересно!
Слайд 4МНОГОГРАННИК
Многогранник - геометрическое тело, ограниченное со всех сторон плоскими
Стороны граней называются ребрами многогранника, а концы ребер — вершинами многогранника
По числу граней различают четырехгранники, пятигранники и т. д.
Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней.
Выпуклый многогранник называется правильным, если все его грани — правильные одинаковые
многоугольники и все многогранные углы при вершинах равны. Существует 5 видов правильных многогранников:
тетраэдр
куб
октаэдр
додекаэдр
икосаэдр.
Слайд 5Мы привыкли видеть как нарезаются продукты питания , а как будет
Слайд 6Вопросы, которые надо обсудить
Что такое многогранник?
Какой многогранник называется выпуклым?
Что такое грань
Что значит построить сечение многогранника плоскостью?
Как могут располагаться относительно друг друга многогранник и плоскость?
Как задается плоскость?
Сколько точек необходимо чтобы однозначно провести прямую на плоскости?
Когда задача на построение сечения многогранника плоскостью считается решенной?
Какая фигура получается при пересечении двух плоскостей
Где располагается точка пересечения плоскости и прямой лежащей в другой плоскости?
Алгоритм построения сечений многогранников
Методы построения сечений многогранников
Слайд 7Цели урока:
Формирование у учащихся навыков решения задач на построение сечений
Обучающая цель:
Обобщить и систематизировать знания, умения и навыки при построении сечений многогранников методом следов.
Закрепление умений и навыков построения сечений различными методами в ходе решения позиционных задач;
Контроль усвоения учащимися знаний и отработка у них умений и навыков в области изучаемой темы.
Развивающая цель: формировать и развивать у учащихся логическое мышление, пространственное воображение, графическую культуру и математическую речь.
Воспитательная цель: воспитывать познавательный интерес к предмету воспитывать чувство сплоченности, взаимопомощи, воспитывать умения работать индивидуально над задачей
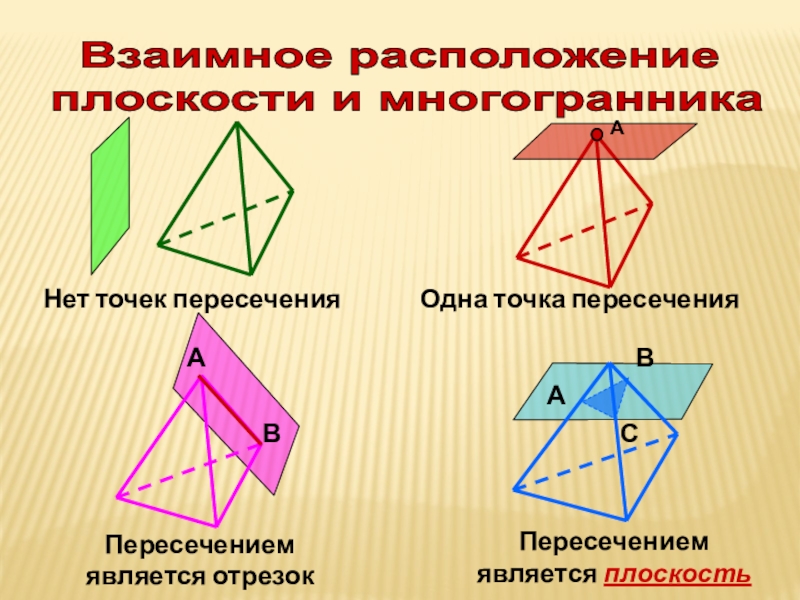
Слайд 8Взаимное расположение
плоскости и многогранника
В
А
Нет точек пересечения
Одна точка пересечения
Пересечением
является отрезок
Пересечением
является плоскость
Слайд 11Секущей плоскостью параллелепипеда (тетраэдра) называется любая плоскость, по обе стороны от
Слайд 12 Построить сечение многогранника плоскостью – это значит указать точки
Для построения сечения многогранника плоскостью нужно в плоскости каждой грани указать 2 точки, принадлежащие сечению, соединить их прямой и найти точки пересечения этой прямой с ребрами многогранника.
Слайд 13Секущая плоскость
сечение
Секущая плоскость пересекает грани тетраэдра по отрезкам.
Многоугольник, сторонами которого
Слайд 14При этом необходимо учитывать следующее:
1. Соединять можно только две точки, лежащие
в
Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками.
2. Секущая плоскость пересекает параллельные грани по параллельным отрезкам.
3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.
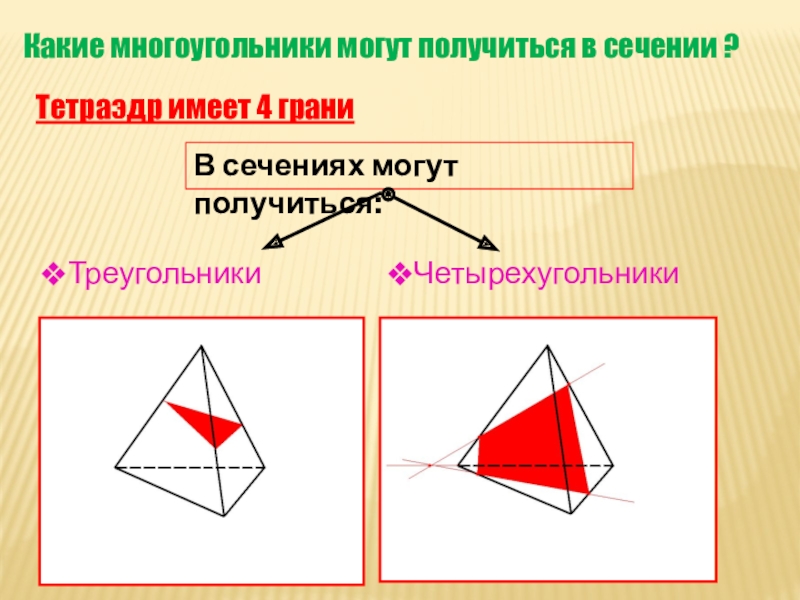
Слайд 15Какие многоугольники могут получиться в сечении ?
Тетраэдр имеет 4 грани
В сечениях
Четырехугольники
Треугольники
Слайд 16Треугольники
Параллелепипед имеет 6 граней
Четырехугольники
Шестиугольники
Пятиугольники
В его сечениях
могут получиться:
Слайд 17Блиц - опрос
Задача блиц – опроса: ответить на вопросы и обосновать
Слайд 18АКСИОМЫ
планиметрия
стереометрия
1. Каждой прямой принадлежат по крайней мере две точки
2. Имеются по
3. Через любые две точки проходит прямая, и притом только одна.
Характеризуют взаимное расположение точек и прямых
Основное понятие геометрии «лежать между»
4. Из трех точек прямой одна и только одна лежит между двумя другими.
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Слайд 21А
В
С
D
А1
D1
С1
B1
Верите ли вы, что прямые НК и МР пересекаются?
N
Р
Н
К
М
Блиц-опрос.
На чертеже
ещё ошибка!
Слайд 22А
В
С
D
А1
D1
С1
B1
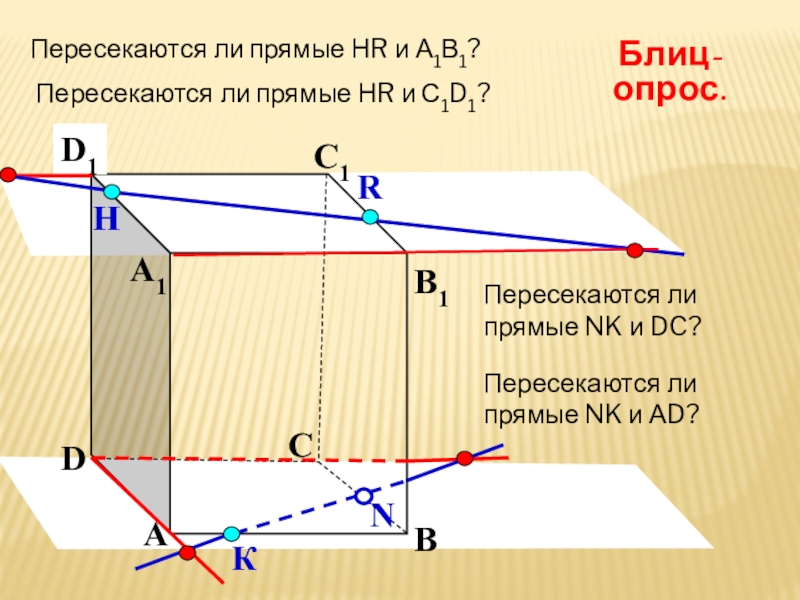
Пересекаются ли прямые НR и А1В1?
N
Н
К
Блиц-опрос.
R
Пересекаются ли прямые НR и
Пересекаются ли
прямые NK и DC?
Пересекаются ли
прямые NK и АD?
Слайд 23Умение решать задачи – практическое искусство, подобное плаванию, или катанию на
Д. Пойа
Как научиться решать задачи?
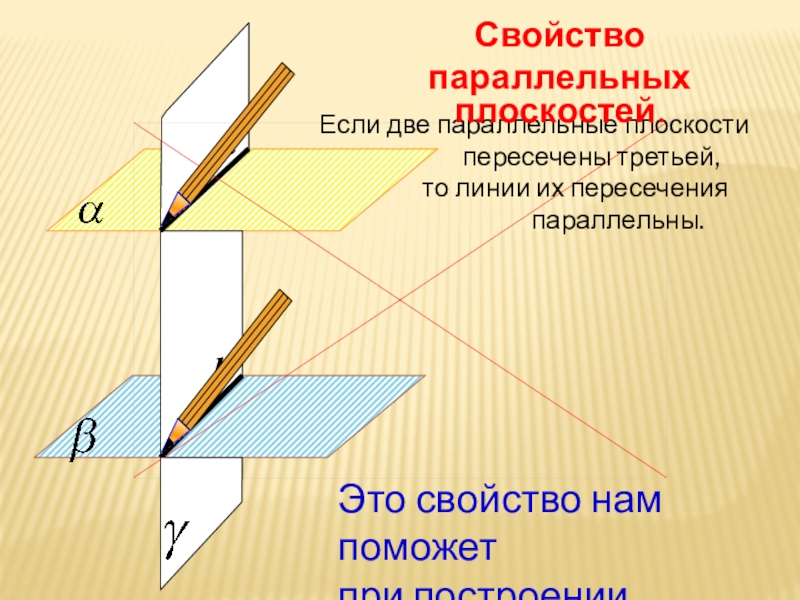
Слайд 24Если две параллельные плоскости
то линии их пересечения
параллельны.
Свойство
параллельных плоскостей.
Это свойство нам поможет
при построении сечений.
Слайд 28 Аксиоматический метод
Метод следов
Суть метода заключается в построении
Слайд 29A
B
C
D
K
L
M
N
F
G
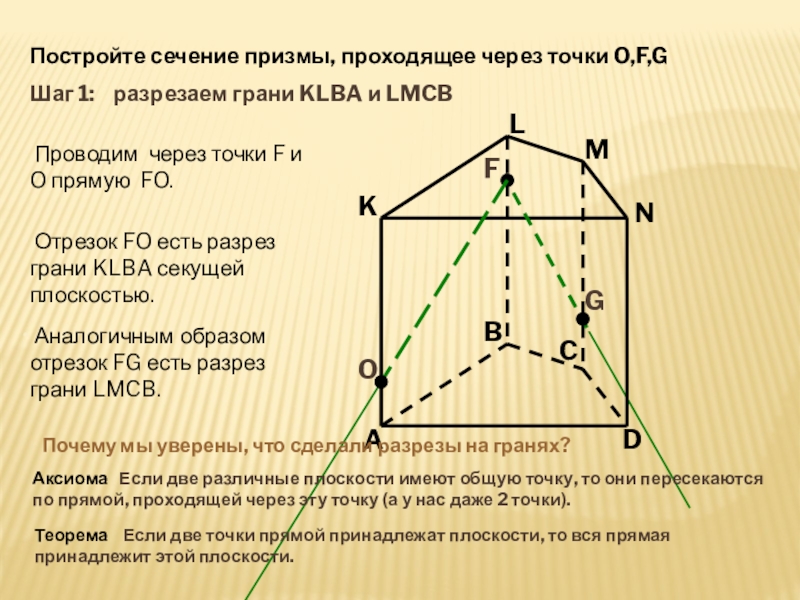
Проводим через точки F и O прямую FO.
O
Отрезок FO есть разрез грани KLBA секущей плоскостью.
Аналогичным образом отрезок FG есть разрез грани LMCB.
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Почему мы уверены, что сделали разрезы на гранях?
Постройте сечение призмы, проходящее через точки O,F,G
Шаг 1: разрезаем грани KLBA и LMCB
Слайд 30A
B
C
D
K
L
M
N
F
G
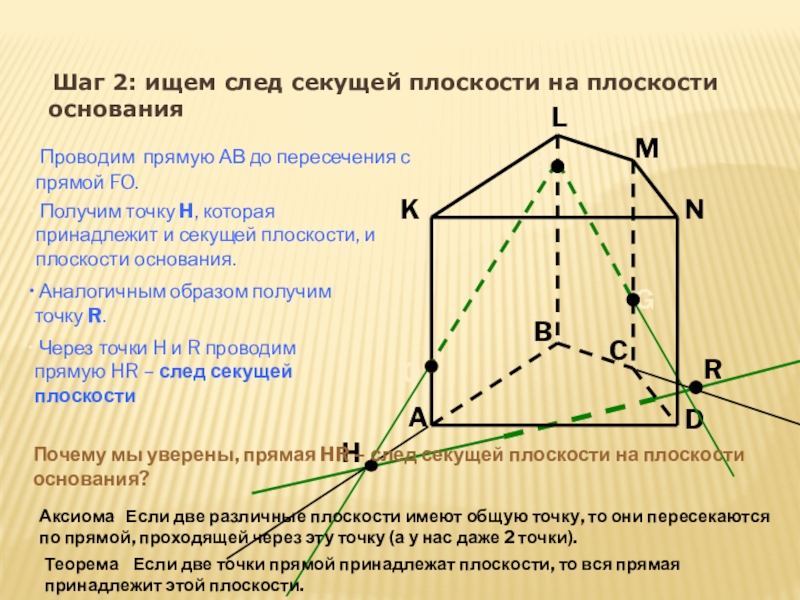
Шаг 2: ищем след секущей плоскости на плоскости основания
Проводим
O
Получим точку H, которая принадлежит и секущей плоскости, и плоскости основания.
Аналогичным образом получим точку R.
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Через точки H и R проводим прямую HR – след секущей плоскости
Почему мы уверены, прямая HR – след секущей плоскости на плоскости основания?
Слайд 31A
B
C
D
K
L
M
N
F
G
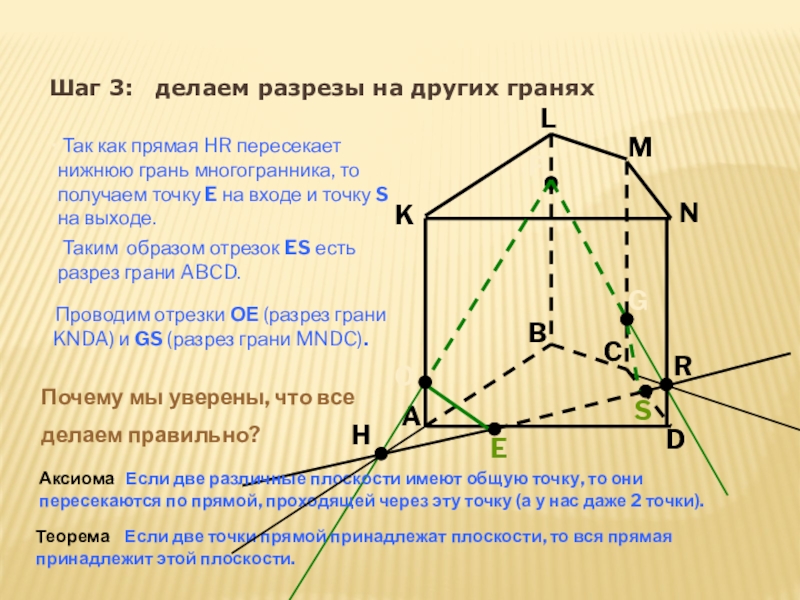
Шаг 3: делаем разрезы на других гранях
Так как прямая
O
Таким образом отрезок ES есть разрез грани ABCD.
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Проводим отрезки ОЕ (разрез грани KNDA) и GS (разрез грани MNDC).
Почему мы уверены, что все
делаем правильно?
Слайд 32C
B
A
D
K
L
M
N
F
G
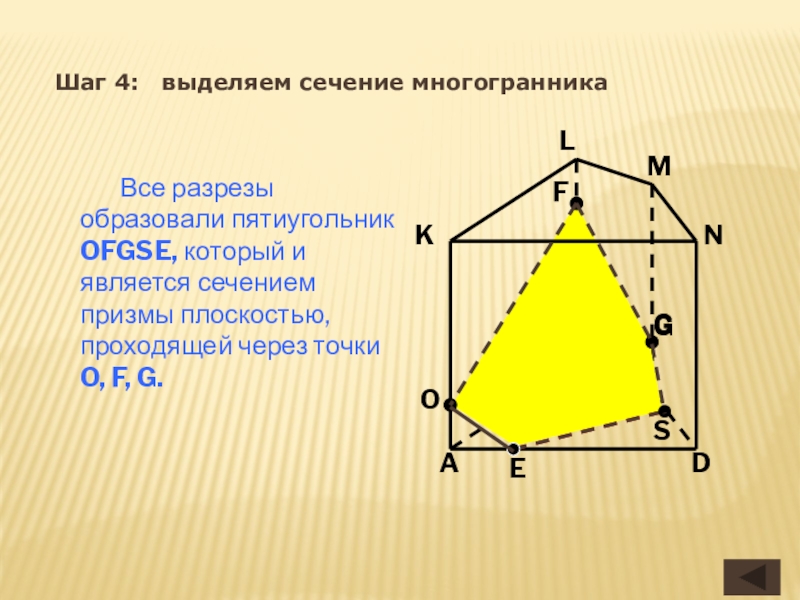
Шаг 4: выделяем сечение многогранника
Все разрезы образовали пятиугольник OFGSE, который
O
G
Слайд 35Правила для самоконтроля:
Вершины сечения находятся только на ребрах.
Стороны сечения находятся только
Секущая плоскость пересекает грань или плоскость грани, то только один раз.
Слайд 37Кроссворд
Бесконечная ровная поверхность
Сторона грани многогранника.
Основное понятие геометрии – место пересечения двух
Точка пересечения ребер многогранника.
Сторона многогранника.
Поверхность, составленная из многоугольников.
Раздел геометрии, изучающий фигуры в пространстве.
П
Л
О
С
К
О
Т
Ь
С
Р
Е
Б
Р
О
Т
Ч
К
О
А
Р
Ш
И
Н
А
В
Е
Г
Р
А
Н
Ь
О
Г
О
Г
Р
М
Н
Н
И
К
С
Т
А
Н
Е
О
М
Е
Т
Е
Р
Я
Р
И
Слайд 38Составить две задачи на построение сечений
Творческое домашнее задание
Слайд 40Если вы хотите научиться плавать, то смело входите в воду, а
(Д. Пойа)
СПАСИБО ЗА УРОК !