Выполнила: учитель математики Пустовалова Е. А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Построение правильных многоугольников с помощью циркуля и линейки.
Содержание
- 1. Построение правильных многоугольников с помощью циркуля и линейки.
- 2. Повторение.Какой многоугольник называется правильным?Приведите примеры правильных многоугольников.Какая
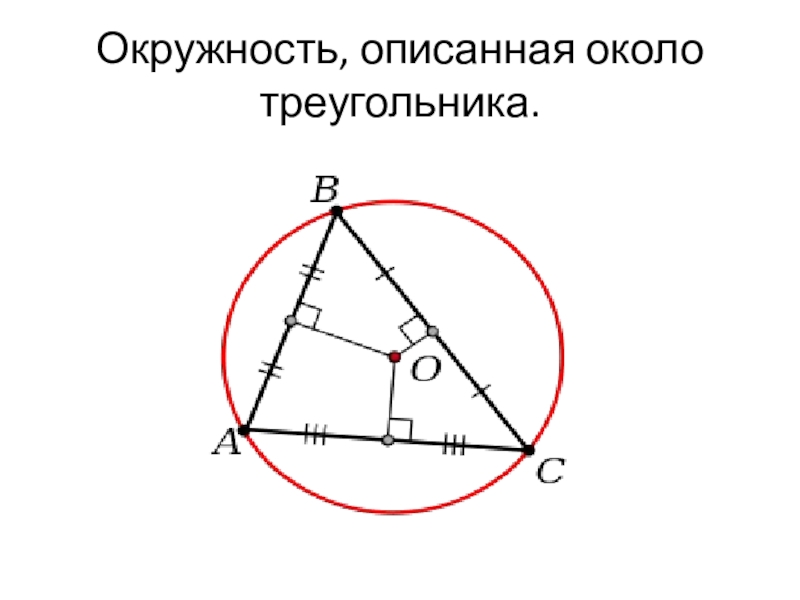
- 3. Окружность, описанная около треугольника.
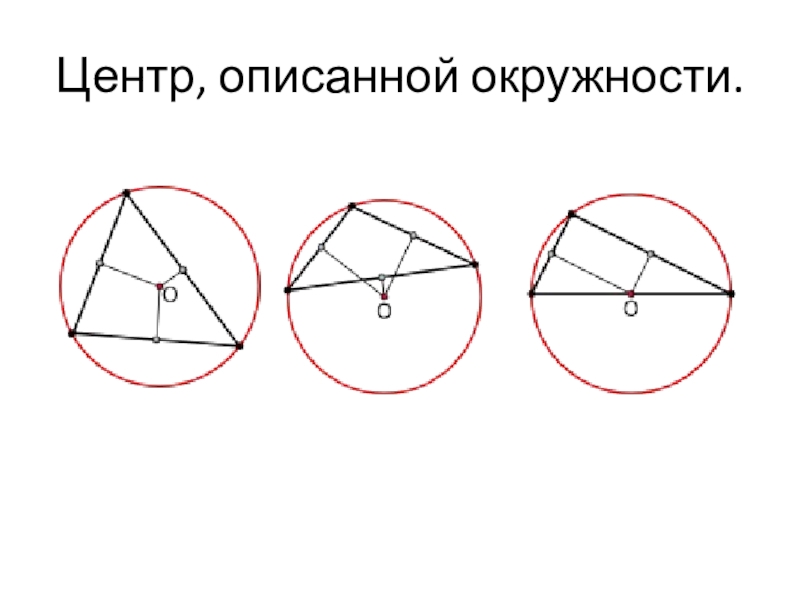
- 4. Центр, описанной окружности.
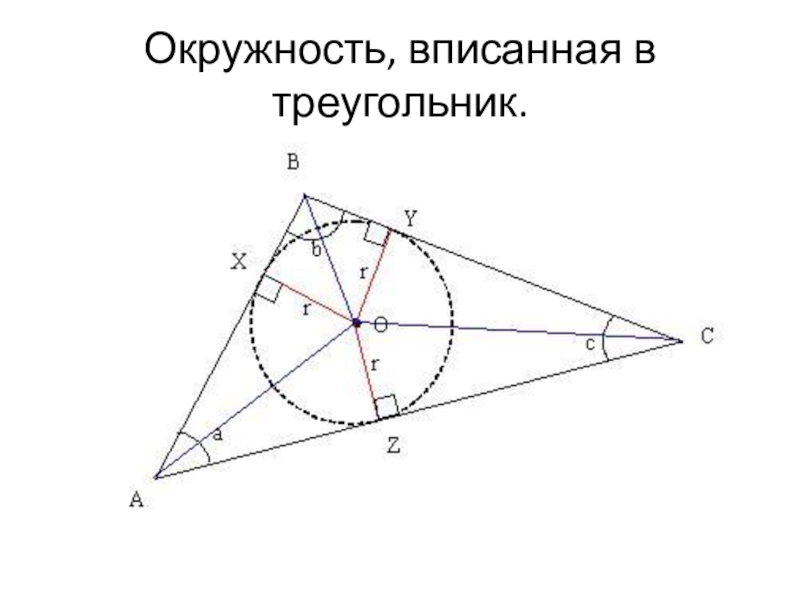
- 5. Окружность, вписанная в треугольник.
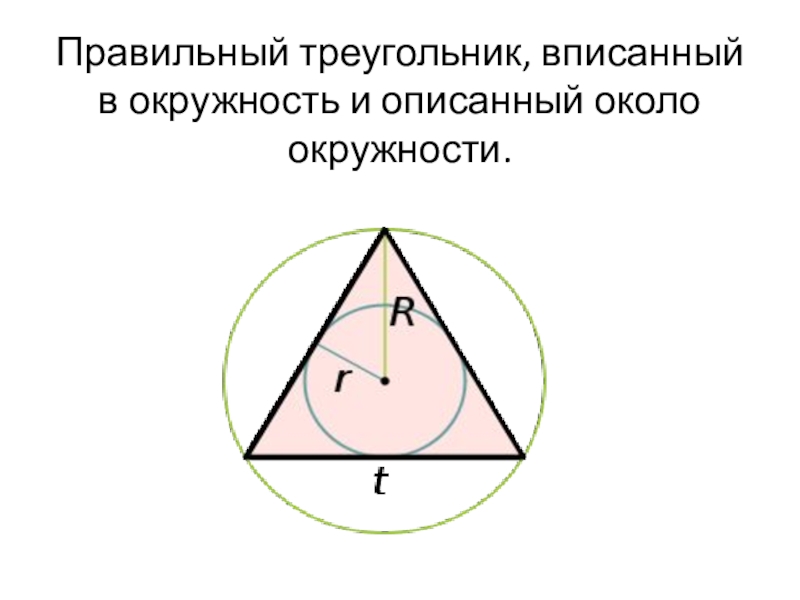
- 6. Правильный треугольник, вписанный в окружность и описанный около окружности.
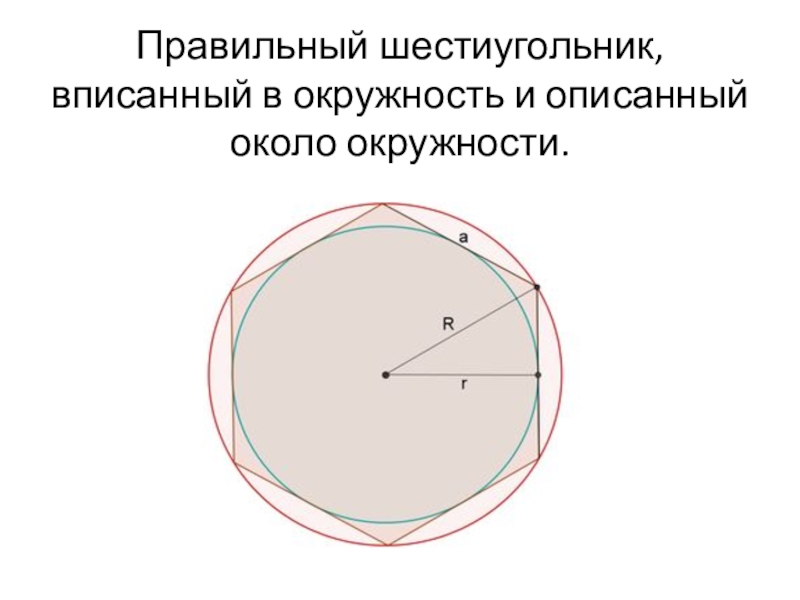
- 7. Правильный шестиугольник, вписанный в окружность и описанный около окружности.
- 8. Центр правильного многоугольника. Центры окружностей ,описанной
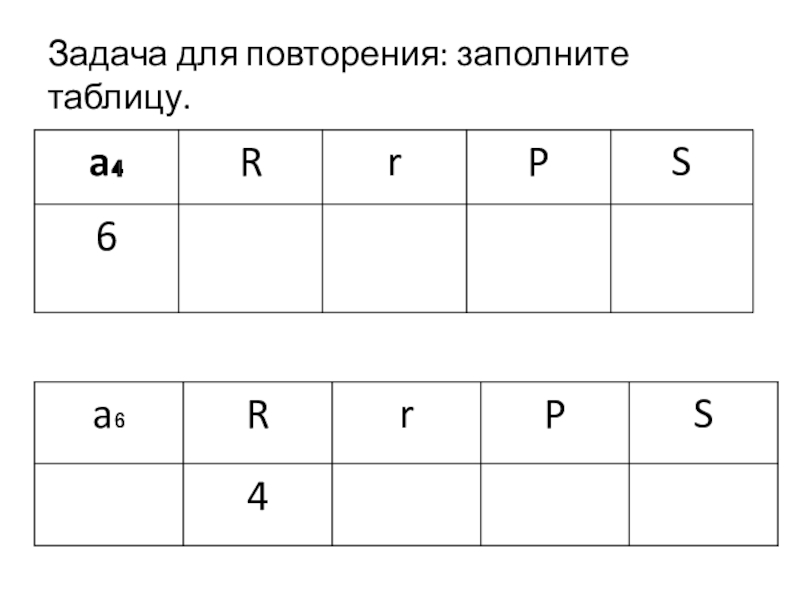
- 9. Задача для повторения: заполните таблицу.
- 10. Новая тема.Построение правильного треугольника.Построение правильного шестиугольника.Построение правильного восьмиугольника.
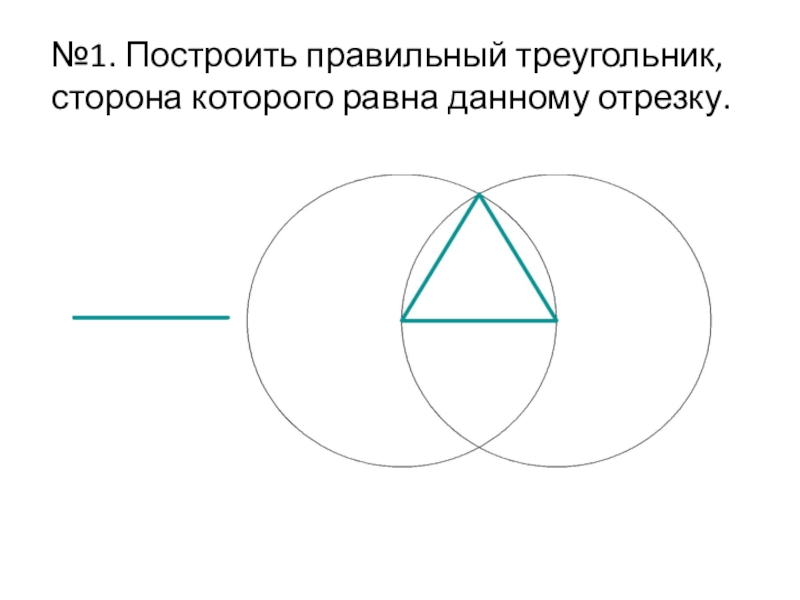
- 11. №1. Построить правильный треугольник, сторона которого равна данному отрезку.
- 12. №2. Построить правильный шестиугольник, сторона которого равна
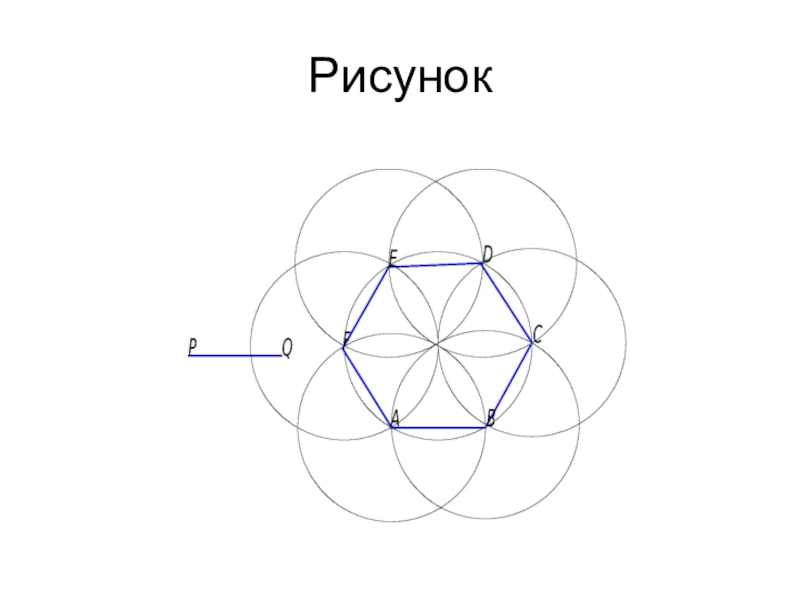
- 13. Рисунок
- 14. №3.Дан правильный 4-угольник. Построить правильный 8-угольник.Дано:Решение:1) Опишем
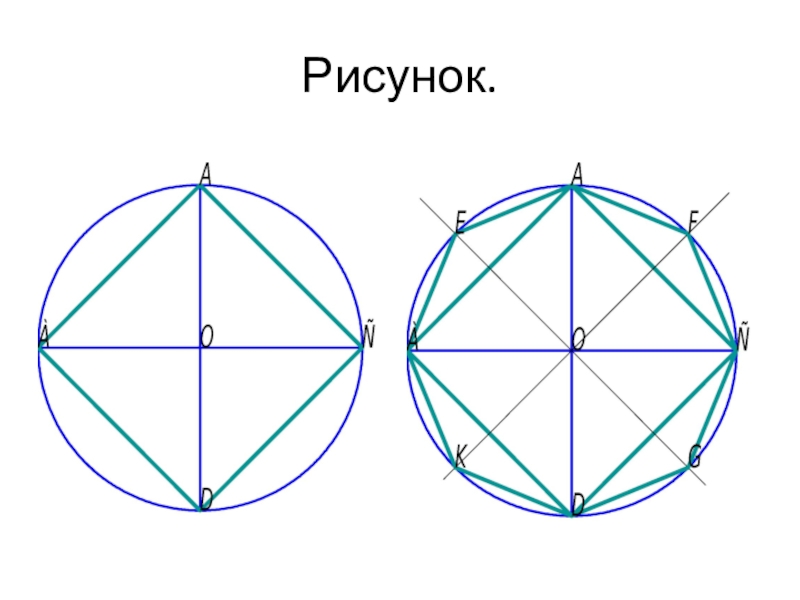
- 15. Рисунок.
- 16. Цепочка построения.4-угольник→8-угольник (8=2*4) → 16-угольник (16=2*8)
- 17. Домашнее задание.Глава 12,§ 1 повторить, пункт 109
- 18. Спасибо за внимание!
Слайд 1 Построение правильных многоугольников с помощью циркуля и линейки в системе компьютерного
Слайд 2Повторение.
Какой многоугольник называется правильным?
Приведите примеры правильных многоугольников.
Какая окружность называется описанной около
Какая окружность называется вписанной в многоугольник?
Слайд 8Центр правильного многоугольника.
Центры окружностей ,описанной около правильного многоугольника и
Слайд 10Новая тема.
Построение правильного треугольника.
Построение правильного шестиугольника.
Построение правильного восьмиугольника.
Слайд 12№2. Построить правильный шестиугольник, сторона которого равна данному отрезку PQ.
Дано :
P
Решение:
1) Воспользуемся формулой а=R (сторона шести-угольника равна радиусу описанной окружности).
2)Построим окружность радиуса PQ;
3)Отметим на окружности произвольную точку А.
4)Построим окружность (А, PQ).
5)Получим точку В.
6) Построим окружность (В, PQ).
7) Получим точку С.
8)Осталось аналогично построить еще 3 точки: D, E, F.
9) Соединим точки отрезками: AB, BC, CD, DE, EF, FA.
10) Получили искомый правильный 6-угольник ABCDEF.
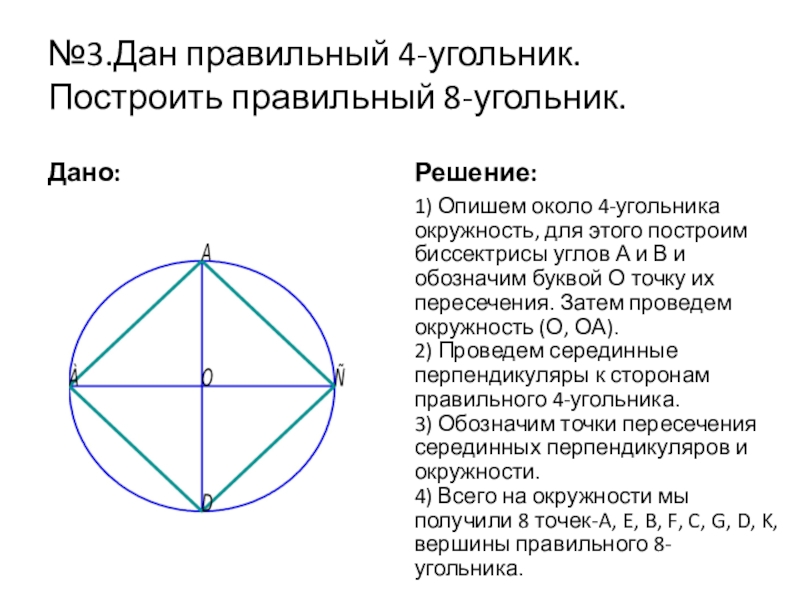
Слайд 14№3.Дан правильный 4-угольник. Построить правильный 8-угольник.
Дано:
Решение:
1) Опишем около 4-угольника окружность, для
2) Проведем серединные перпендикуляры к сторонам правильного 4-угольника.
3) Обозначим точки пересечения серединных перпендикуляров и окружности.
4) Всего на окружности мы получили 8 точек-A, E, B, F, C, G, D, K, вершины правильного 8-угольника.
Слайд 17Домашнее задание.
Глава 12,§ 1 повторить, пункт 109 учить.
На листе формата А₄
№1094.