(1,2)
№24 (1,2)
№25 (1,2)
№26 (1,2)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Подготовка к ОГЭ модуль алгебра , геометрия 2 часть
Содержание
- 1. Подготовка к ОГЭ модуль алгебра , геометрия 2 часть
- 2. Модуль «Алгебра»
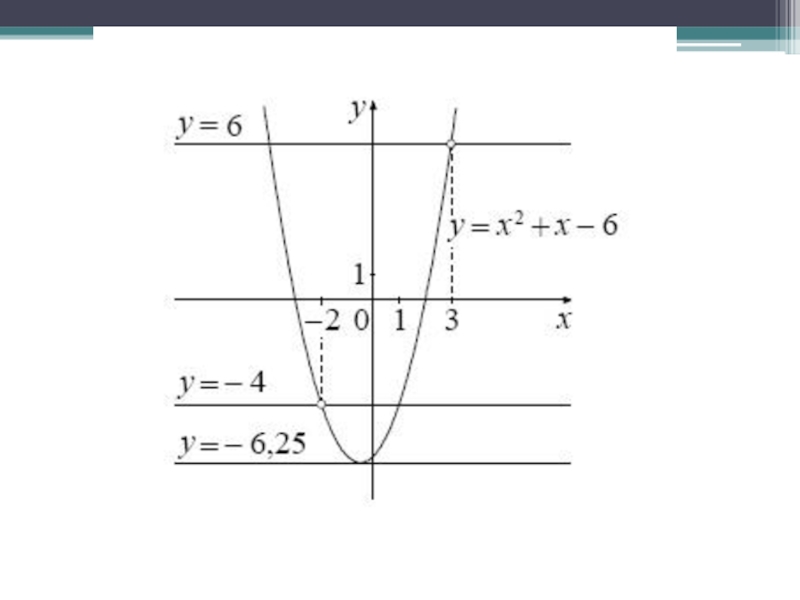
- 3. Задание 23 Постройте график функции и определите, при каких значениях параметра прямая имеет с графиком ровно одну общую точку.
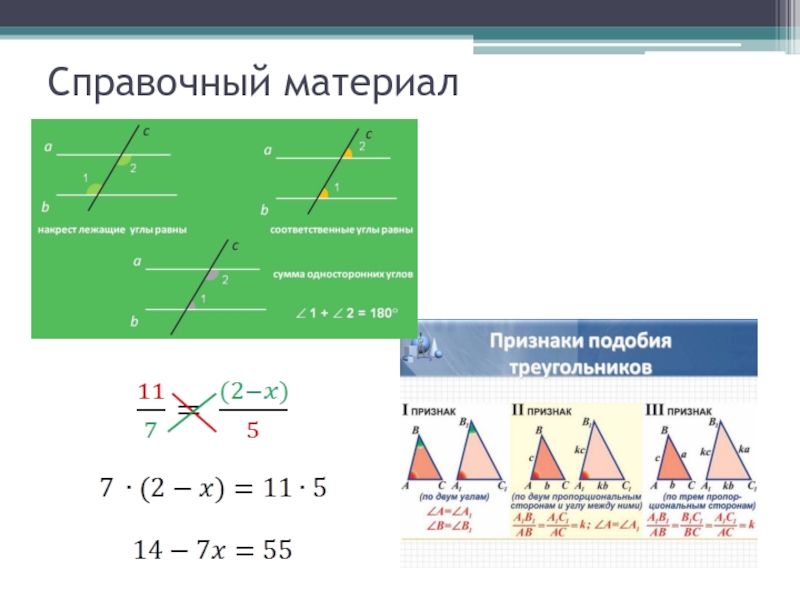
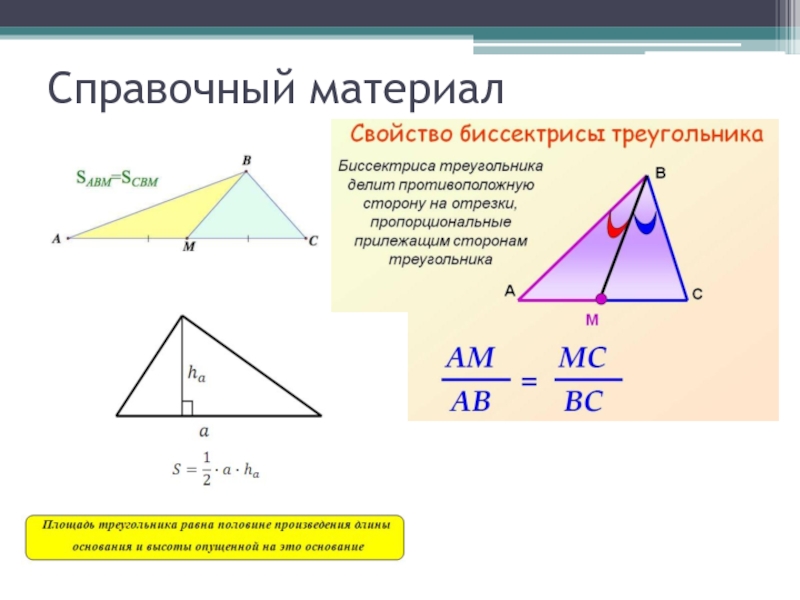
- 4. Справочный материал
- 5. Слайд 5
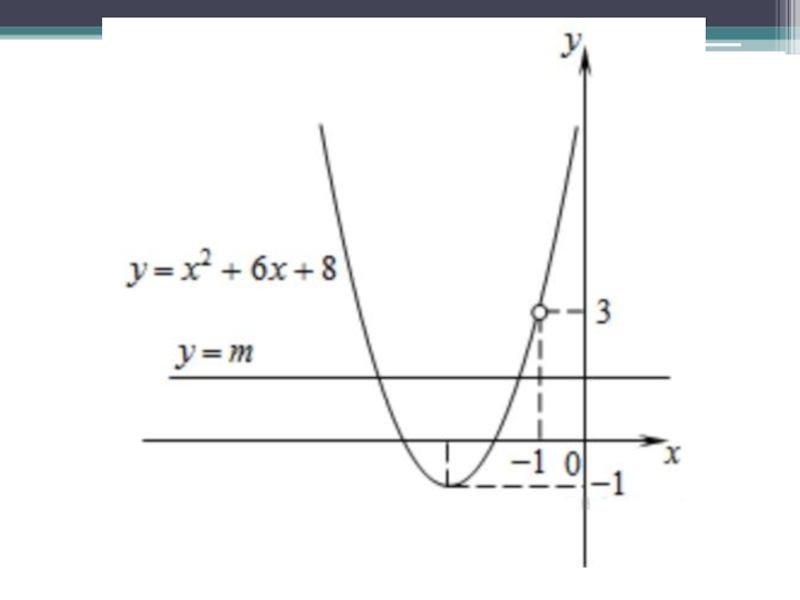
- 6. Задание 23Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно одну общую точку.
- 7. Слайд 7
- 8. Слайд 8
- 9. Модуль «Геометрия»
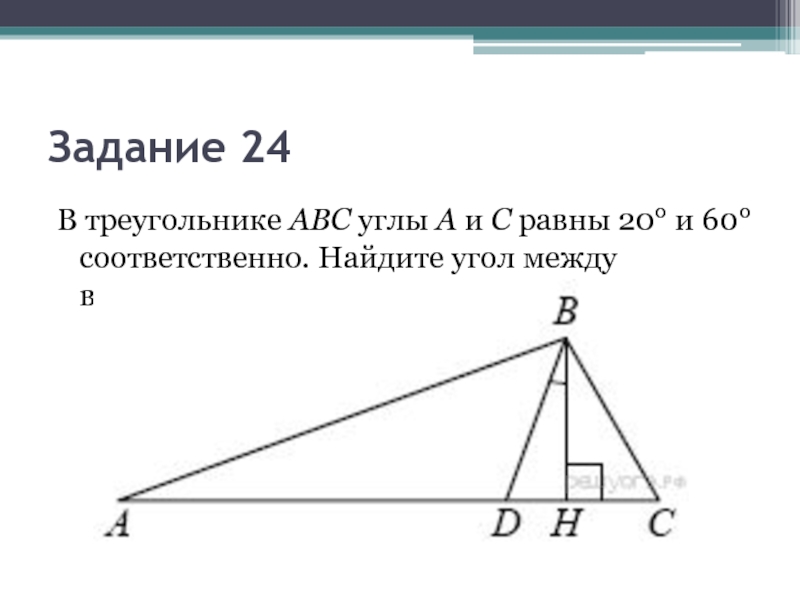
- 10. Задание 24В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
- 11. Справочный материал
- 12. Задание 24 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 13, AC = 65, NC = 28.
- 13. Справочный материал
- 14. Задание 25 Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1равны.
- 15. Справочный материал
- 16. Задание 25Докажите, что биссектрисы углов при основании равнобедренного треугольника равны.
- 17. Справочный материал
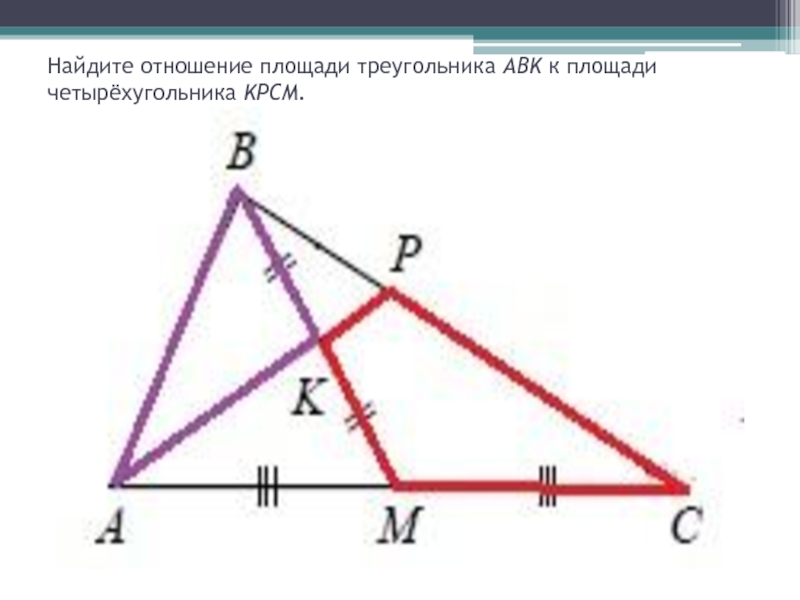
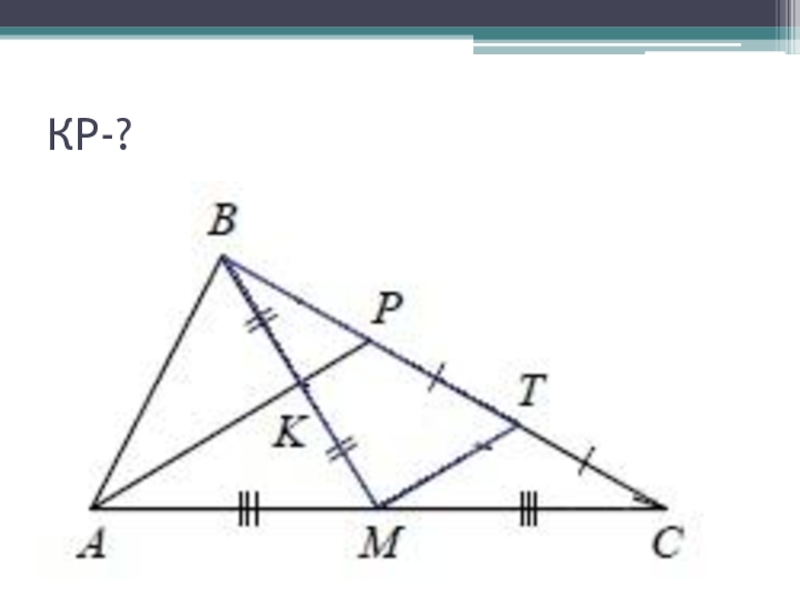
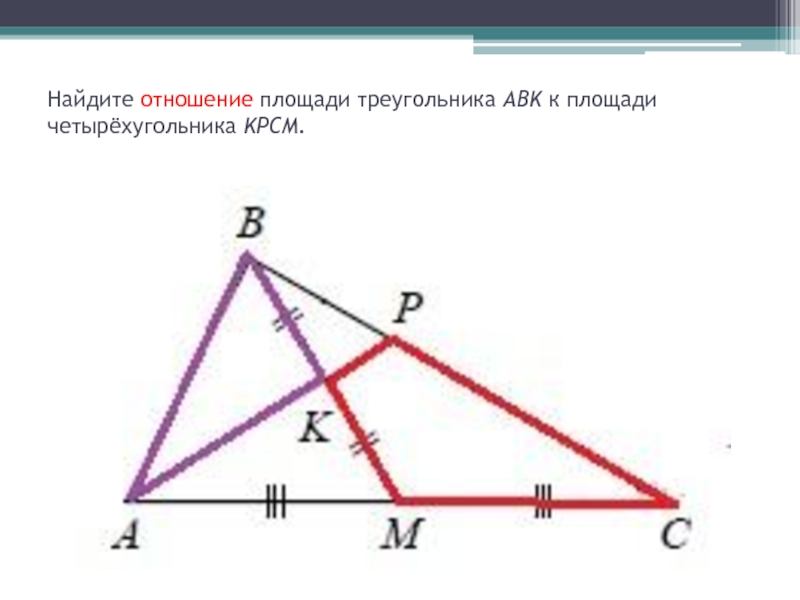
- 18. Задание 26Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону
- 19. Справочный материал
- 20. Слайд 20
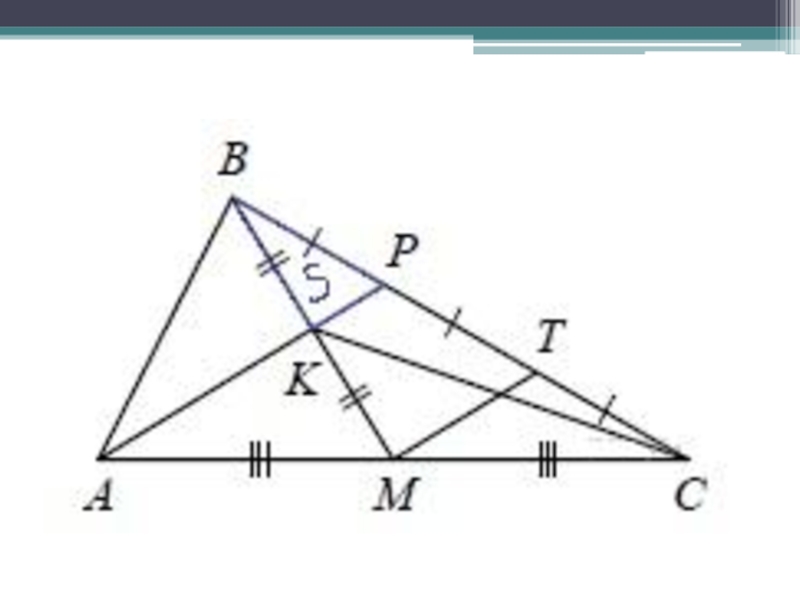
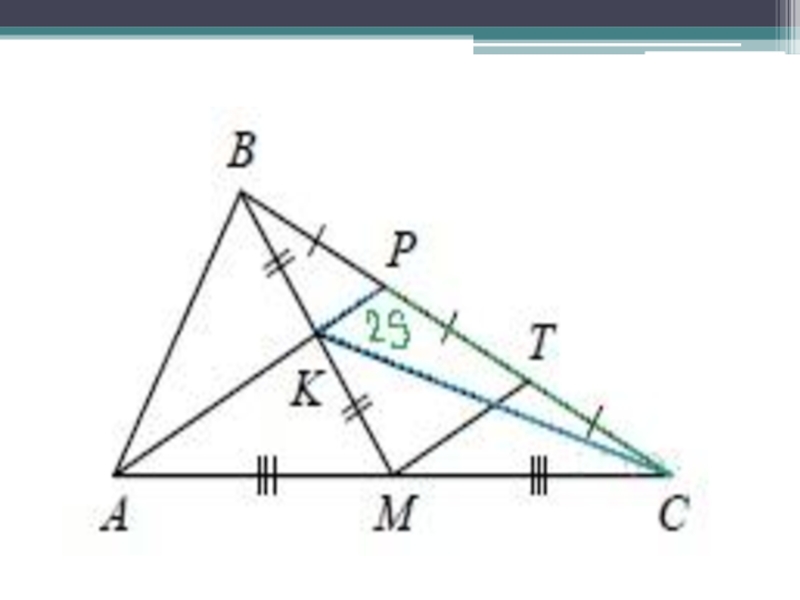
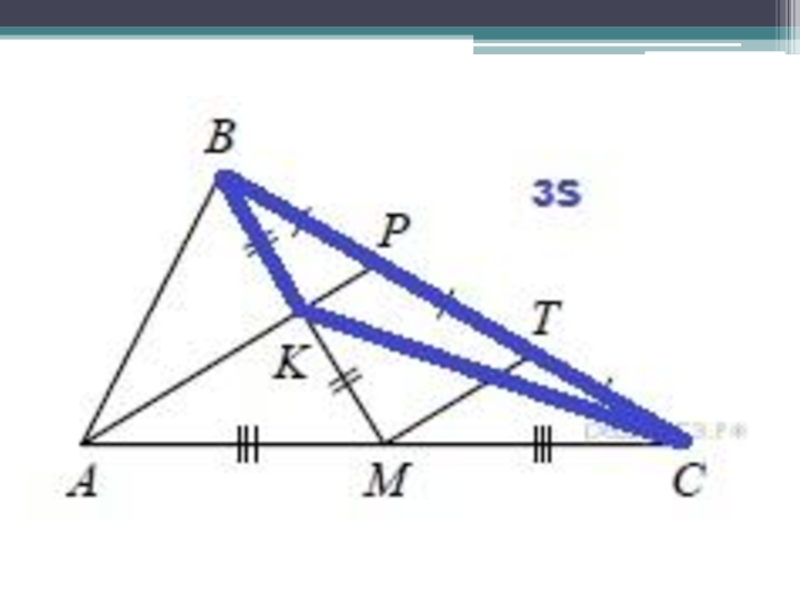
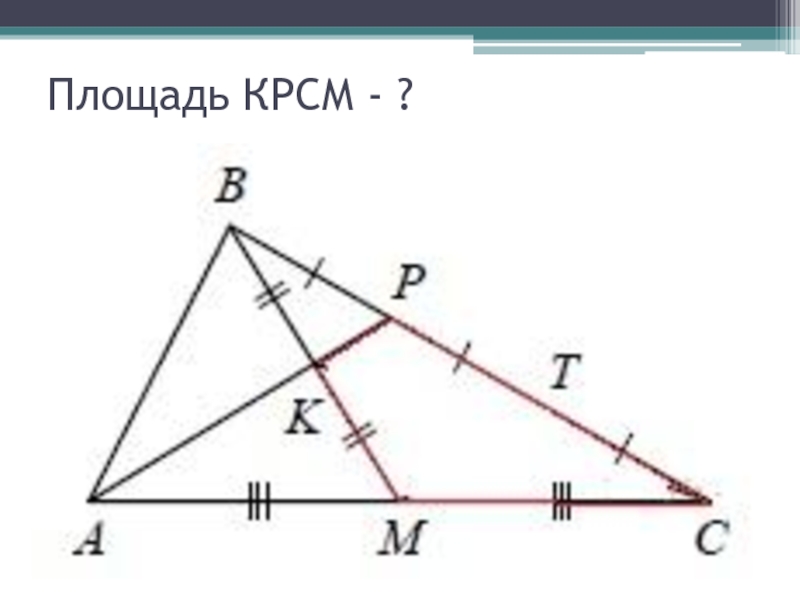
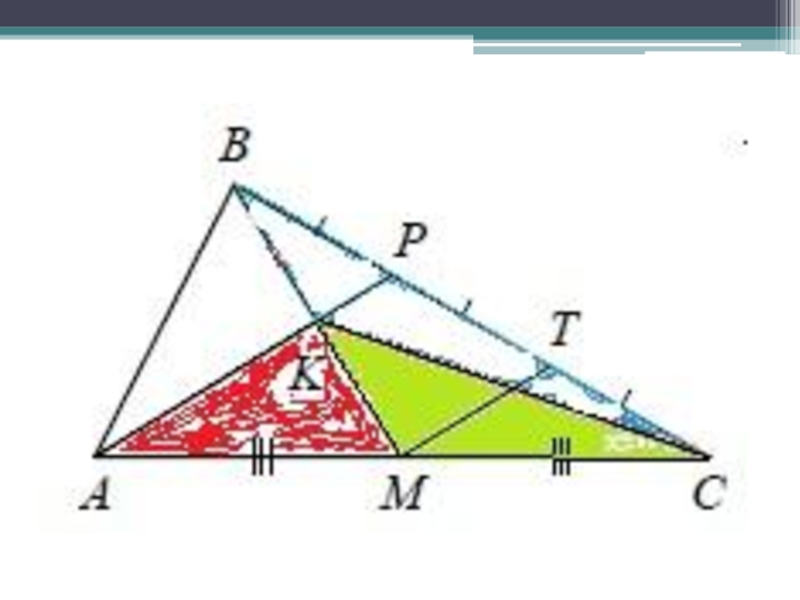
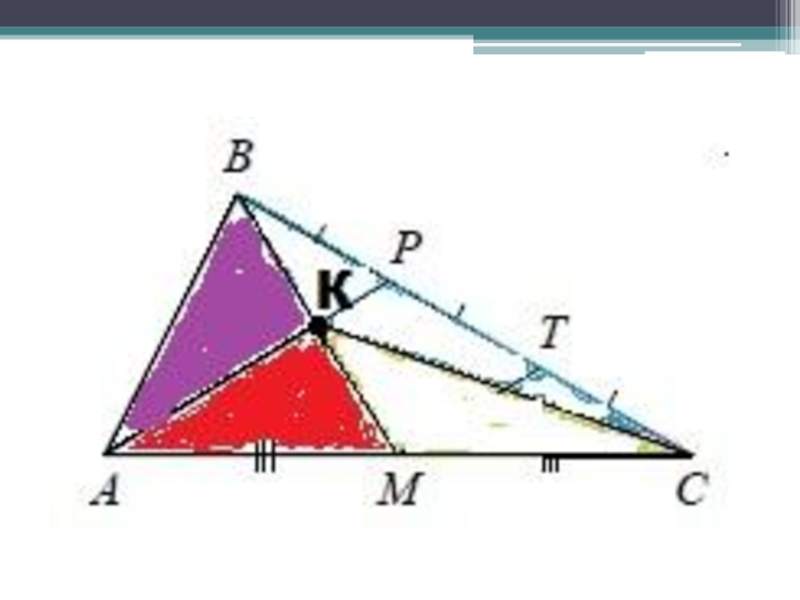
- 21. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
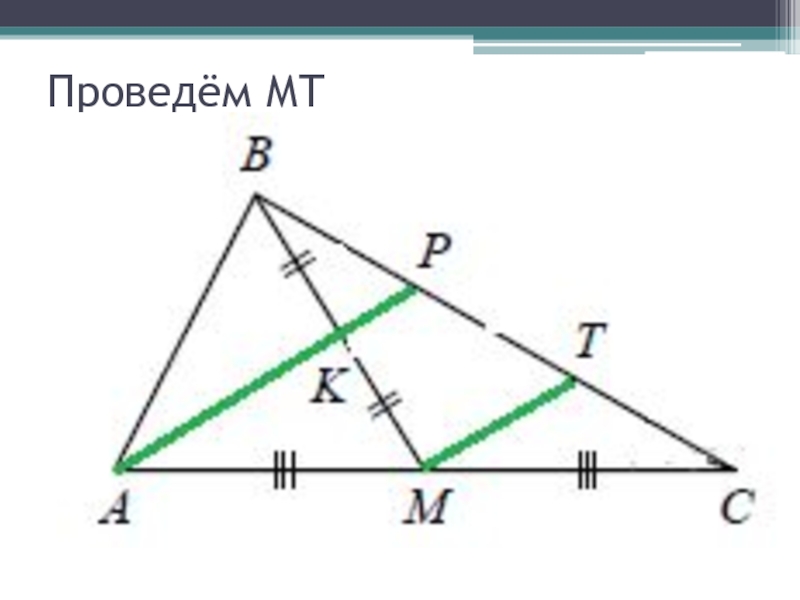
- 22. Проведём МТ
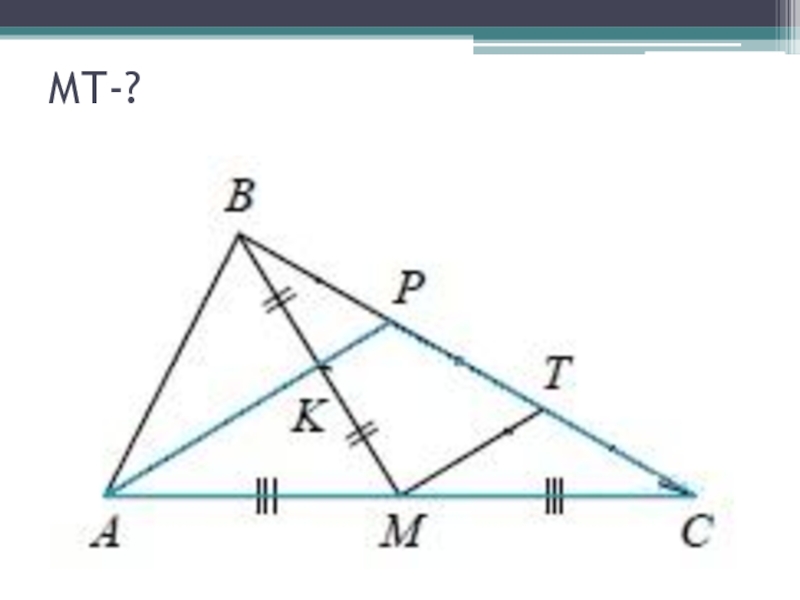
- 23. МТ-?
- 24. КР-?
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
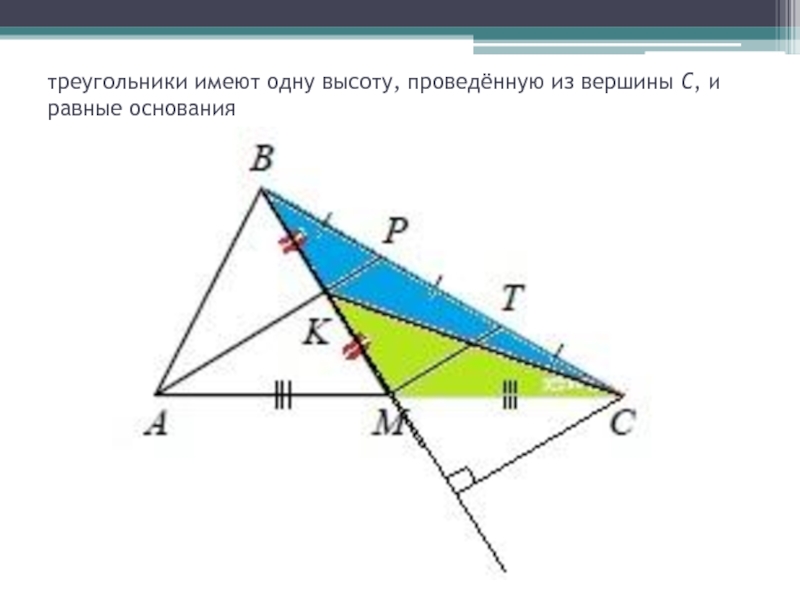
- 28. треугольники имеют одну высоту, проведённую из вершины С, и равные основания
- 29. Площадь КРСМ - ?
- 30. Слайд 30
- 31. Слайд 31
- 32. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
- 33. Задание 26Площадь треугольника ABC равна 80. Биссектриса AD пересекает медиану BK в точке E, при этом BD:CD=1:3. Найдите площадь четырехугольника EDCK.
- 34. Справочный материал
- 35. Слайд 35
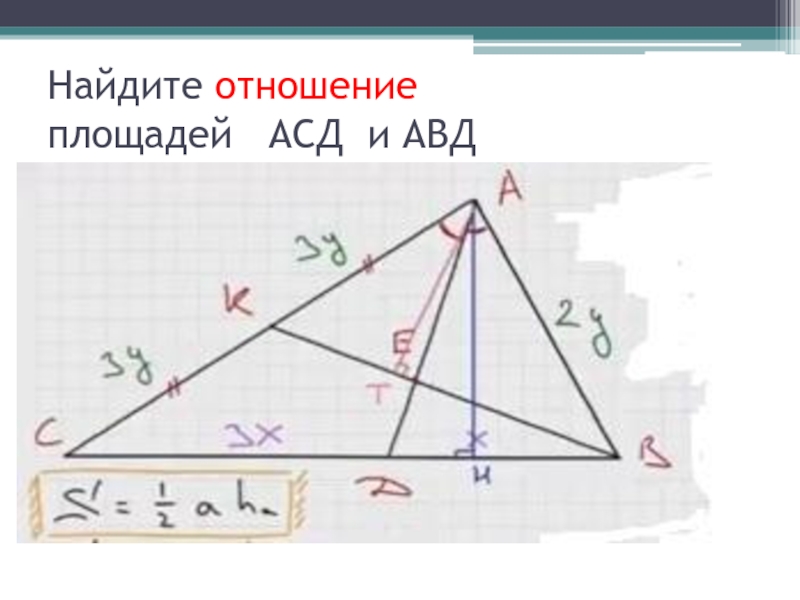
- 36. Найдите отношение площадей АСД и АВД
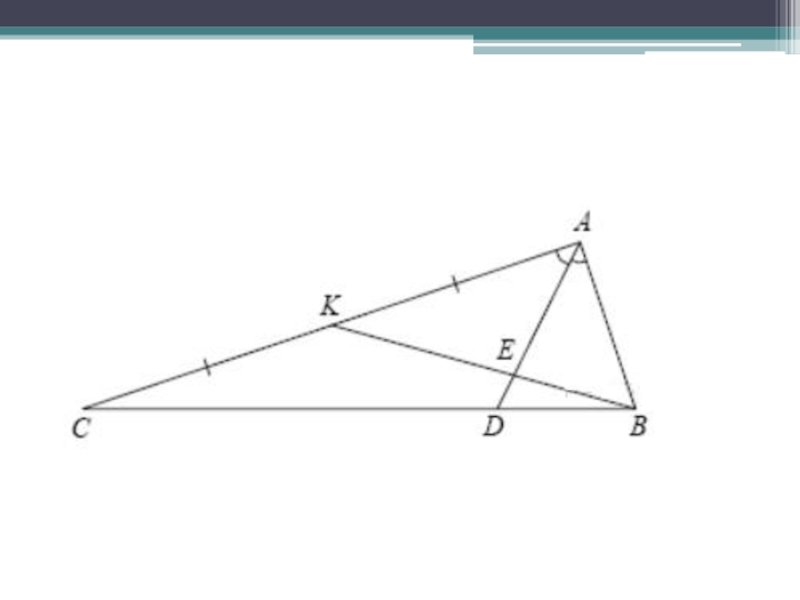
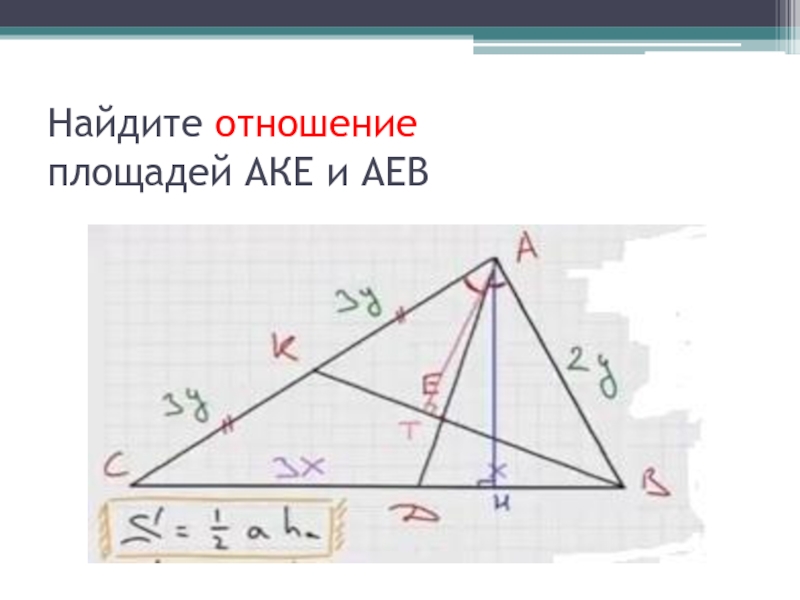
- 37. Найдите отношение площадей АКЕ и АЕВ
- 38. Слайд 38
Модуль «Алгебра»
Слайд 1Подготовка к ОГЭ
Автор: учитель математики
МОБУ «Троицкая СОШ»
Шуринова Екатерина Викторовна
План
№23
Слайд 3Задание 23
Постройте график функции и определите, при каких значениях параметра прямая имеет с графиком
ровно одну общую точку.
Слайд 6Задание 23
Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно
одну общую точку.
Слайд 10Задание 24
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и
биссектрисой BD.
Слайд 12Задание 24
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 13, AC = 65, NC = 28.
Слайд 14Задание 25
Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1равны.
Слайд 18Задание 26
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P.
Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Слайд 33Задание 26
Площадь треугольника ABC равна 80. Биссектриса AD пересекает медиану BK в точке E, при этом BD:CD=1:3. Найдите площадь
четырехугольника EDCK.