- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Подготовка к ГИА по математике Все о треугольниках
Содержание
- 1. Подготовка к ГИА по математике Все о треугольниках
- 2. СодержаниеОпределение, элементы, внешний уголВиды треугольниковПризнаки равенства треугольниковПризнаки
- 3. Треугольник – фигура, состоящая из трёх
- 4. Виды треугольниковОстроугольный – все углы острыеПрямоугольный –
- 5. Признаки равенства треугольников1. По двум сторонам и
- 6. Признаки равенства прямоугольных треугольников1. По двум катетам
- 7. Признаки подобия треугольников1. По двум углам Если
- 8. Признаки подобия прямоугольных треугольников 1. По острому углуЕсли
- 9. Медиана треугольникаМедиана треугольника – отрезок, соединяющий вершину
- 10. Свойства медиан треугольника1. Медианы точкой пересечения делятся
- 11. Свойства медиан треугольникаЕсли О – точка пересечения
- 12. Биссектриса треугольникаБиссектриса треугольника – отрезок биссектрисы угла треугольника от вершины угла до противолежащей стороны.
- 13. Свойства биссектрис треугольника1. Биссектрисы треугольника пересекаются в
- 14. Высота треугольникаВысота треугольника – перпендикуляр, проведенный из вершины треугольника к прямой, на которой лежит противолежащая сторона.
- 15. Свойства высот треугольника1. Высоты треугольника или их
- 16. Свойства высот треугольника3. Высота на сторону с
- 17. Средняя линия треугольникаСредняя линия треугольника – отрезок,
- 18. Свойства треугольников1. Сумма углов треугольника равна 180°2.
- 19. Свойства треугольников5. Прямая СD делит ∆АВС на
- 20. Свойства треугольников6. Теорема синусов Стороны треугольника пропорциональны
- 21. Свойства треугольников 7. Теорема косинусов Квадрат
- 22. Соотношение между сторонами и углами треугольникаВ треугольнике:
- 23. Свойства равнобедренного треугольника1. В равнобедренном треугольнике углы
- 24. Свойства равнобедренного треугольника3. В равнобедренном треугольнике медианы
- 25. Свойства прямоугольного треугольника1. Гипотенуза больше катета2. Сумма
- 26. Свойства прямоугольного треугольника5. Высота, опущенная из
- 27. Свойства прямоугольного треугольника7. Пропорциональные отрезки в прямоугольном
- 28. б) Каждый катет есть среднее пропорциональное
- 29. Свойства прямоугольного треугольника8. Тригонометрические функции острого угла
- 30. Свойства подобных треугольников1. У подобных треугольников АВС и А1В1С1: 1)
- 31. Свойства подобных треугольников2. Отношение периметров подобных треугольников
- 32. Формулы площади треугольникаПроизвольный треугольник: S =
- 33. ИсточникиЛ.С. Атанасян. Учебник геометрии 7-9.М.: «Просвещение», 2009
СодержаниеОпределение, элементы, внешний уголВиды треугольниковПризнаки равенства треугольниковПризнаки подобия треугольниковМедиана, свойства медианБиссектриса, свойства биссектрисВысота, свойства высотСредняя линия треугольникаСвойства треугольников Соотношение между сторонами и углами треугольникаСвойства равнобедренного треугольникаСвойства прямоугольного треугольникаСвойства подобных треугольниковФормулы площади треугольника
Слайд 2Содержание
Определение, элементы, внешний угол
Виды треугольников
Признаки равенства треугольников
Признаки подобия треугольников
Медиана, свойства медиан
Биссектриса,
свойства биссектрис
Высота, свойства высот
Средняя линия треугольника
Свойства треугольников
Соотношение между сторонами и углами треугольника
Свойства равнобедренного треугольника
Свойства прямоугольного треугольника
Свойства подобных треугольников
Формулы площади треугольника
Высота, свойства высот
Средняя линия треугольника
Свойства треугольников
Соотношение между сторонами и углами треугольника
Свойства равнобедренного треугольника
Свойства прямоугольного треугольника
Свойства подобных треугольников
Формулы площади треугольника
Слайд 3
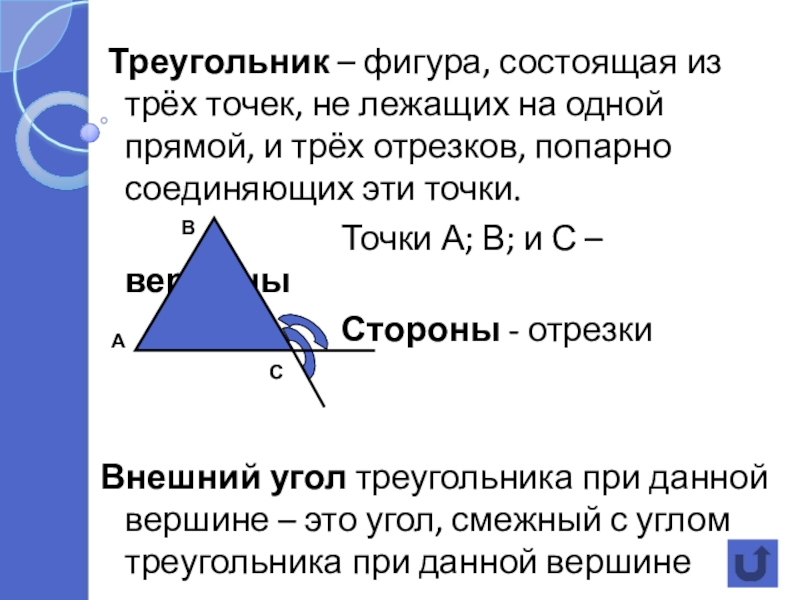
Треугольник – фигура, состоящая из трёх точек, не лежащих на
одной прямой, и трёх отрезков, попарно соединяющих эти точки.
Точки А; В; и С – вершины
Стороны - отрезки
Внешний угол треугольника при данной вершине – это угол, смежный с углом треугольника при данной вершине
Точки А; В; и С – вершины
Стороны - отрезки
Внешний угол треугольника при данной вершине – это угол, смежный с углом треугольника при данной вершине
А
В
С
Слайд 4Виды треугольников
Остроугольный – все углы острые
Прямоугольный – один угол прямой
Тупоугольный –
один угол тупой
Разносторонний – все стороны разной длины
Равнобедренный – две стороны (боковые) равны
Равносторонний – все стороны равны (правильный)
Разносторонний – все стороны разной длины
Равнобедренный – две стороны (боковые) равны
Равносторонний – все стороны равны (правильный)
Слайд 5Признаки равенства треугольников
1. По двум сторонам и углу между ними
Если АВ = А1 В1 ТО ∆ АВС= ∆ А1 В1С1
АС =А1С1
<А = <А1
2. По стороне и прилежащим к ней углам
Если АВ = А1 В1 ТО ∆ АВС= ∆ А1 В1С1
<А = <А1
<в = <в1
3. По трём сторонам
Если АВ = А1 В1 ТО ∆ АВС= ∆ А1 В1С1
ВС = В1 С1
АС = А1 С1
АС =А1С1
<А = <А1
2. По стороне и прилежащим к ней углам
Если АВ = А1 В1 ТО ∆ АВС= ∆ А1 В1С1
<А = <А1
<в = <в1
3. По трём сторонам
Если АВ = А1 В1 ТО ∆ АВС= ∆ А1 В1С1
ВС = В1 С1
АС = А1 С1
Слайд 6Признаки равенства прямоугольных треугольников
1. По двум катетам
Если АС
=А1С1 ТО ∆ АВС= ∆ А1 В1С1
ВС=В1С1
2. По катету и острому углу
Если АС =А1С1 ТО ∆ АВС= ∆ А1 В1С1
<А = <А1
3. По гипотенузе и острому углу
Если АВ = А1 В1 ТО ∆ АВС= ∆ А1 В1С1
<А = <А1
4. По гипотенузе и катету
Если АВ = А1 В1 ТО ∆ АВС= ∆ А1 В1С1
АС =А1С1
ВС=В1С1
2. По катету и острому углу
Если АС =А1С1 ТО ∆ АВС= ∆ А1 В1С1
<А = <А1
3. По гипотенузе и острому углу
Если АВ = А1 В1 ТО ∆ АВС= ∆ А1 В1С1
<А = <А1
4. По гипотенузе и катету
Если АВ = А1 В1 ТО ∆ АВС= ∆ А1 В1С1
АС =А1С1
А
А1
В
В1
С
С1
Слайд 7Признаки подобия треугольников
1. По двум углам
Если
<В = <В1, то ∆ АВС ~ ∆ А1 В1С1
2. По двум сторонам и углу между ними
Если АВ/А1В1 = АС/А1С1; <А = <А1 то
∆ АВС ~ ∆ А1 В1С1
3. По трем сторонам
Если АВ/А1В1 = АС/А1С1 = ВС/В1С1, то
∆ АВС ~ ∆ А1 В1С1
2. По двум сторонам и углу между ними
Если АВ/А1В1 = АС/А1С1; <А = <А1 то
∆ АВС ~ ∆ А1 В1С1
3. По трем сторонам
Если АВ/А1В1 = АС/А1С1 = ВС/В1С1, то
∆ АВС ~ ∆ А1 В1С1
Слайд 8Признаки подобия прямоугольных треугольников
1. По острому углу
Если
то ∆ АВС ~ ∆ А1 В1С1
2. По двум катетам
АС/А1С1 = ВС/В1С1, то ∆ АВС ~ ∆ А1 В1С1
3. По гипотенузе и катету
АВ/А1В1 = АС/А1С1, то ∆ АВС ~ ∆ А1 В1С1
2. По двум катетам
АС/А1С1 = ВС/В1С1, то ∆ АВС ~ ∆ А1 В1С1
3. По гипотенузе и катету
АВ/А1В1 = АС/А1С1, то ∆ АВС ~ ∆ А1 В1С1
А
А1
В
В1
С
С1
Слайд 9Медиана треугольника
Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей
стороны
Медианы пересекаются в одной точке (центр тяжести треугольника).
Медианы пересекаются в одной точке (центр тяжести треугольника).
Слайд 10Свойства медиан треугольника
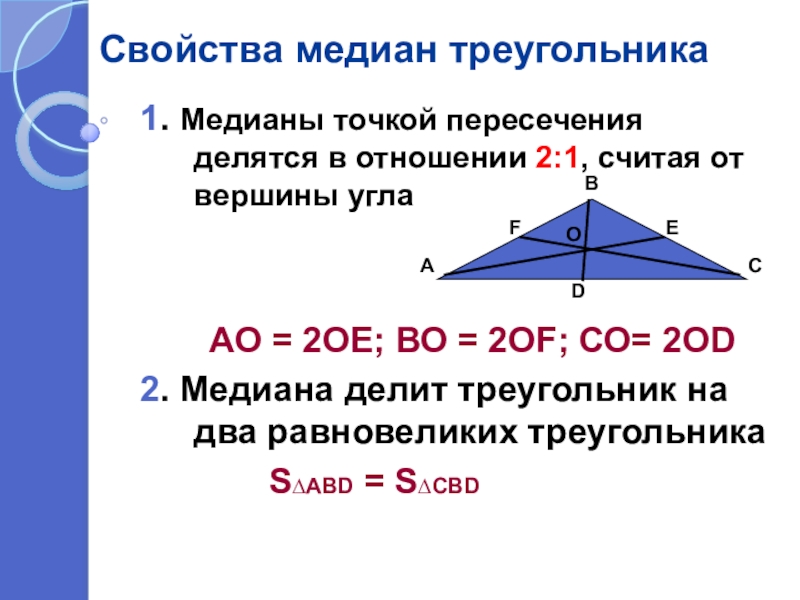
1. Медианы точкой пересечения делятся в отношении 2:1, считая
от вершины угла
АО = 2ОЕ; ВО = 2ОF; СО= 2ОD
2. Медиана делит треугольник на два равновеликих треугольника
S∆АВD = S∆СВD
АО = 2ОЕ; ВО = 2ОF; СО= 2ОD
2. Медиана делит треугольник на два равновеликих треугольника
S∆АВD = S∆СВD
А
В
С
О
Е
F
D
Слайд 11Свойства медиан треугольника
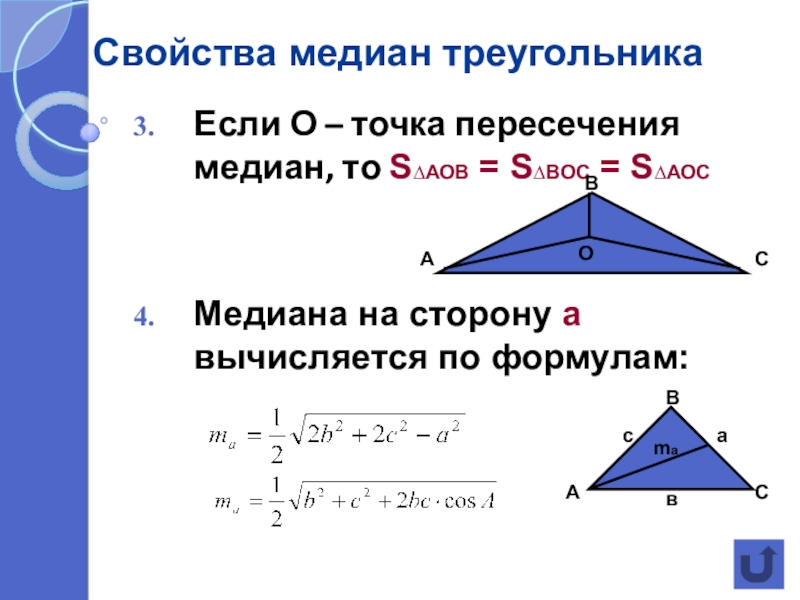
Если О – точка пересечения медиан, то S∆АОВ =
S∆ВОС = S∆АОС
Медиана на сторону а вычисляется по формулам:
Медиана на сторону а вычисляется по формулам:
А
В
С
О
А
В
С
а
в
с
ma
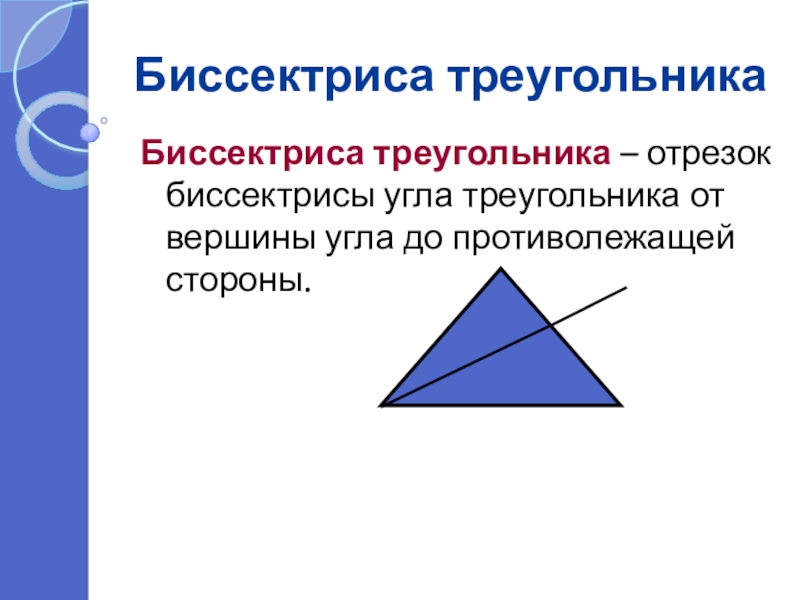
Слайд 12Биссектриса треугольника
Биссектриса треугольника – отрезок биссектрисы угла треугольника от вершины угла
до противолежащей стороны.
Слайд 13Свойства биссектрис треугольника
1. Биссектрисы треугольника пересекаются в одной точке – центре
вписанной в треугольник окружности
2. Если СD – биссектриса угла С ∆АВС, то: 1) АD : ВD=АС : ВС
2) S∆АСD : S∆ВСD=АС : ВС
2. Если СD – биссектриса угла С ∆АВС, то: 1) АD : ВD=АС : ВС
2) S∆АСD : S∆ВСD=АС : ВС
А
В
С
D
Слайд 14Высота треугольника
Высота треугольника – перпендикуляр, проведенный из вершины треугольника к прямой,
на которой лежит противолежащая сторона.
Слайд 15Свойства высот треугольника
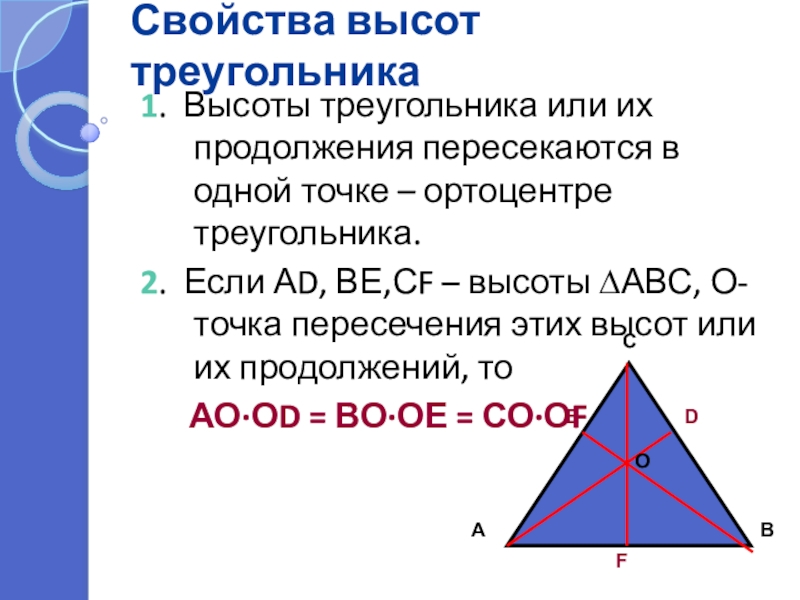
1. Высоты треугольника или их продолжения пересекаются в одной
точке – ортоцентре треугольника.
2. Если АD, ВЕ,СF – высоты ∆АВС, О- точка пересечения этих высот или их продолжений, то
АО·ОD = ВО·ОЕ = СО·ОF
2. Если АD, ВЕ,СF – высоты ∆АВС, О- точка пересечения этих высот или их продолжений, то
АО·ОD = ВО·ОЕ = СО·ОF
А
С
В
D
Е
F
О
Слайд 16Свойства высот треугольника
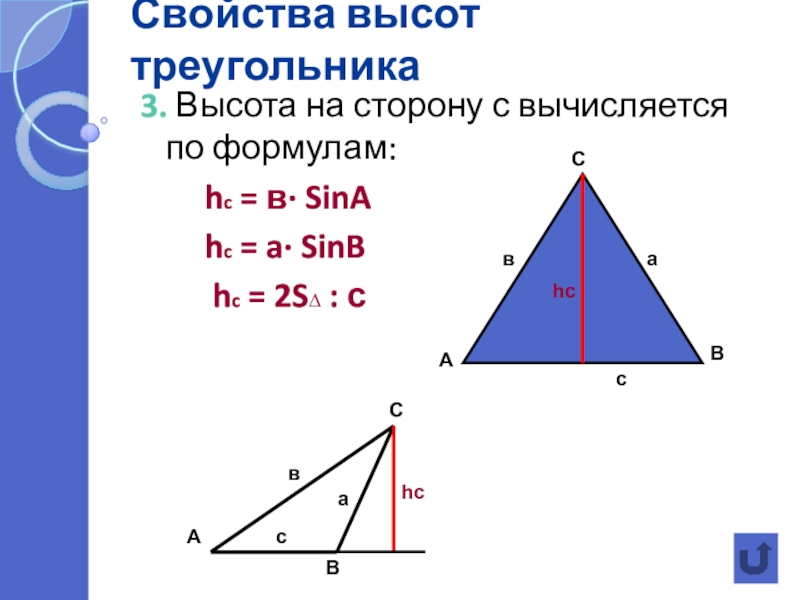
3. Высота на сторону с вычисляется по формулам:
hc = в· SinA
hc = a· SinB
hc = 2S∆ : с
hc = a· SinB
hc = 2S∆ : с
А
В
С
а
в
с
hc
hc
А
С
В
а
в
с
Слайд 17Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух сторон
треугольника
Свойство средней линии:
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
MN II AB и MN=1/2·AB
Свойство средней линии:
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
MN II AB и MN=1/2·AB
M
N
Слайд 18Свойства треугольников
1. Сумма углов треугольника равна 180°
2. Внешний угол треугольника равен
сумме двух углов треугольника, не смежных с ним.
3. В треугольнике против большей стороны лежит больший угол, против большего угла – большая сторона.
4. Неравенство треугольника.
Каждая сторона треугольника меньше суммы двух других его сторон
3. В треугольнике против большей стороны лежит больший угол, против большего угла – большая сторона.
4. Неравенство треугольника.
Каждая сторона треугольника меньше суммы двух других его сторон
Слайд 19Свойства треугольников
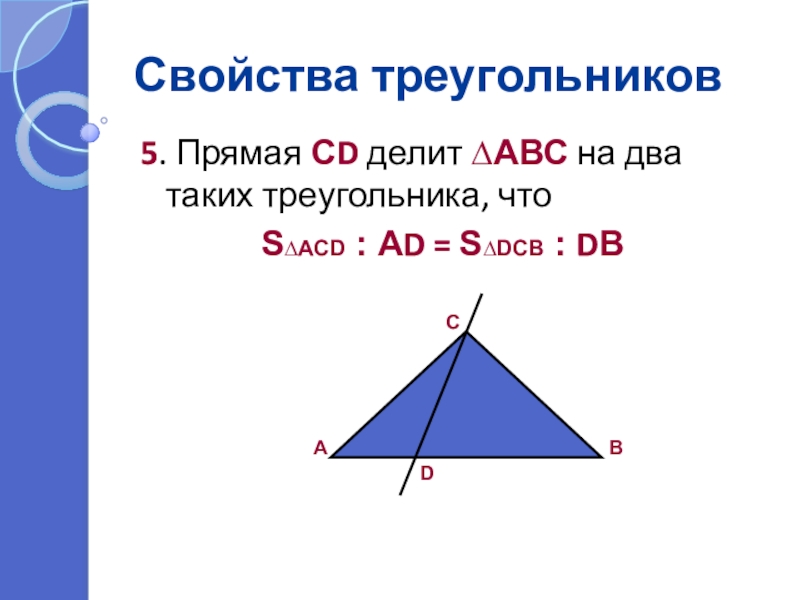
5. Прямая СD делит ∆АВС на два таких треугольника, что
S∆АСD : АD = S∆DСВ : DВ
А
В
С
D
Слайд 20Свойства треугольников
6. Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов:
а : SinA = b : SinB = c : SinC = 2R
где R – радиус окружности, описанной около треугольника
где R – радиус окружности, описанной около треугольника
Слайд 21Свойства треугольников
7. Теорема косинусов
Квадрат любой стороны треугольника равен
сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:
а² = в² + с² - 2вс·СоsА
в² = а² + с² - 2ас·СоsВ
с² = а² + в² - 2ав·СоsС
а² = в² + с² - 2вс·СоsА
в² = а² + с² - 2ас·СоsВ
с² = а² + в² - 2ав·СоsС
Слайд 22Соотношение между сторонами и углами треугольника
В треугольнике:
1) против большей стороны
лежит больший угол;
2) обратно, против большего угла
лежит большая сторона
3) В прямоугольном треугольнике
гипотенуза больше катета
4) Если два угла треугольника равны, то треугольник равнобедренный
2) обратно, против большего угла
лежит большая сторона
3) В прямоугольном треугольнике
гипотенуза больше катета
4) Если два угла треугольника равны, то треугольник равнобедренный
Слайд 23Свойства равнобедренного треугольника
1. В равнобедренном треугольнике углы при основании равны
2. В
равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Слайд 24Свойства равнобедренного треугольника
3. В равнобедренном треугольнике медианы (соответственно высоты и биссектрисы),
проведенные из вершин при основании, равны.
Слайд 25Свойства прямоугольного треугольника
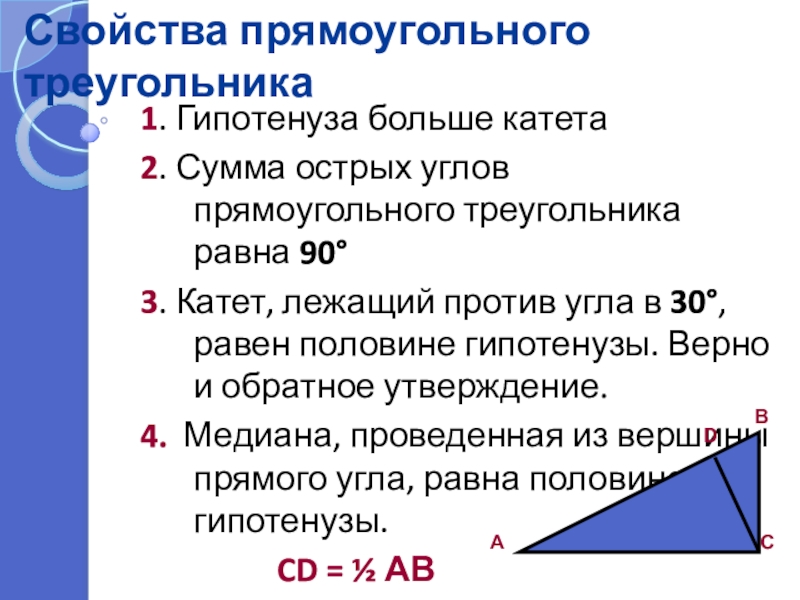
1. Гипотенуза больше катета
2. Сумма острых углов прямоугольного треугольника
равна 90°
3. Катет, лежащий против угла в 30°, равен половине гипотенузы. Верно и обратное утверждение.
4. Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
CD = ½ АВ
3. Катет, лежащий против угла в 30°, равен половине гипотенузы. Верно и обратное утверждение.
4. Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
CD = ½ АВ
А
В
С
D
Слайд 26 Свойства прямоугольного треугольника
5. Высота, опущенная из прямого угла делит прямоугольный
треугольник на два подобных треугольника, которые подобны и исходному треугольнику
6. Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
с² = а² + в²
Египетский треугольник: 3; 4 и 5
Пифагоровы треугольники: 5; 12 и 13
8; 15 и 17 7; 24 и 25
6. Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
с² = а² + в²
Египетский треугольник: 3; 4 и 5
Пифагоровы треугольники: 5; 12 и 13
8; 15 и 17 7; 24 и 25
с
а
в
h
Слайд 27Свойства прямоугольного треугольника
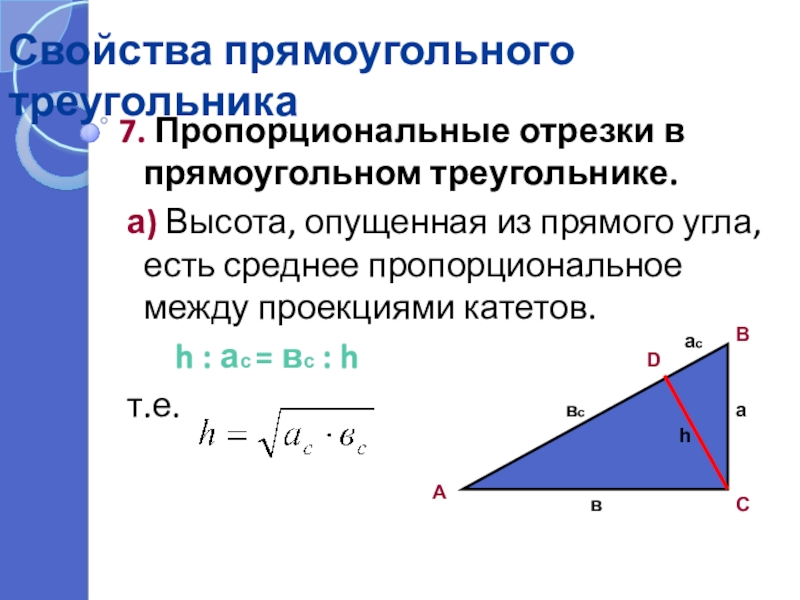
7. Пропорциональные отрезки в прямоугольном треугольнике.
а) Высота, опущенная
из прямого угла, есть среднее пропорциональное между проекциями катетов.
h : ас = вс : h
т.е.
h : ас = вс : h
т.е.
А
В
С
D
а
в
h
вс
ас
Слайд 28
б) Каждый катет есть среднее пропорциональное между гипотенузой и проекцией
катета на гипотенузу:
а : с = ас : а, т.е.
в : с = вс : в, т.е.
в) Высота, опущенная на гипотенузу, делит гипотенузу на отрезки, которые относятся так же как относятся квадраты прилежащих катетов:
ас : вс = а² : в²
а : с = ас : а, т.е.
в : с = вс : в, т.е.
в) Высота, опущенная на гипотенузу, делит гипотенузу на отрезки, которые относятся так же как относятся квадраты прилежащих катетов:
ас : вс = а² : в²
а
в
ас
вс
Слайд 29Свойства прямоугольного треугольника
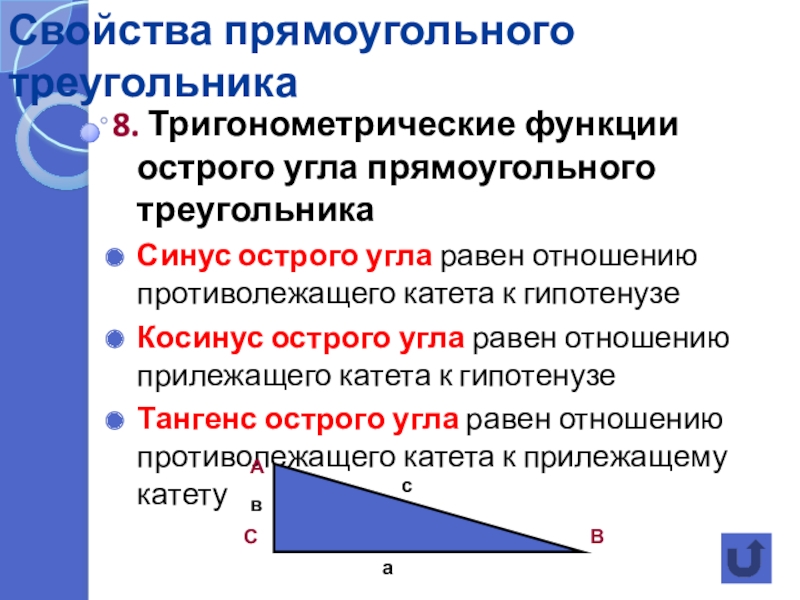
8. Тригонометрические функции острого угла прямоугольного треугольника
Синус острого угла
равен отношению противолежащего катета к гипотенузе
Косинус острого угла равен отношению прилежащего катета к гипотенузе
Тангенс острого угла равен отношению противолежащего катета к прилежащему катету
Косинус острого угла равен отношению прилежащего катета к гипотенузе
Тангенс острого угла равен отношению противолежащего катета к прилежащему катету
А
В
С
в
а
с
Слайд 30 Свойства подобных треугольников
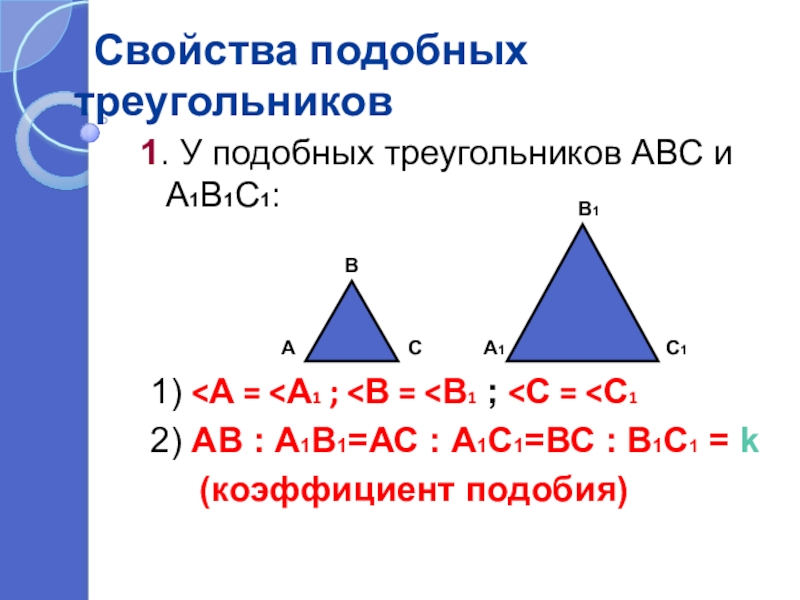
1. У подобных треугольников АВС и А1В1С1:
1)
<А = <А1 ; <В = <В1 ; <С = <С1
2) АВ : А1В1=АС : А1С1=ВС : В1С1 = k
(коэффициент подобия)
2) АВ : А1В1=АС : А1С1=ВС : В1С1 = k
(коэффициент подобия)
А
В
С
А1
В1
С1
Слайд 31Свойства подобных треугольников
2. Отношение периметров подобных треугольников равно коэффициенту подобия.
P∆ABC : P∆A1B1C1 = k
3. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S∆ABC : S∆A1B1C1 = k²
3. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S∆ABC : S∆A1B1C1 = k²
Слайд 32Формулы площади треугольника
Произвольный треугольник:
S = ½ · аhа =
½ · вhв = ½ · сhс ;
S = ½·ab·SinС= ½· aс·SinВ= ½· вс·SinА;
где р- полупериметр
Прямоугольный треугольник:
S = ½ · ав, где а и в - катеты
Правильный треугольник:
S = (а²√3) : 4
S = ½·ab·SinС= ½· aс·SinВ= ½· вс·SinА;
где р- полупериметр
Прямоугольный треугольник:
S = ½ · ав, где а и в - катеты
Правильный треугольник:
S = (а²√3) : 4
Слайд 33Источники
Л.С. Атанасян. Учебник геометрии 7-9.М.: «Просвещение», 2009 г.
Т.С. Степанова. Математика. Весь
школьный курс в таблицах., Минск, «Букмастер»,2012
https://www.google.com/search?hl=ru&site=imghp&tbm=isch&source=hp&biw=1382&bih=732&q=%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0&oq=%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0&gs_l=img.1.0.0l10.11499.13684.0.20805.10.7.0.3.3.0.113.481.6j1.7.0...0.0...1ac.1.7.img.ZRxa7gaF-MI#imgrc=hBP2SMLPpmMX9M%3A%3BLrDnnfsdseyC3M%3Bhttp%253A%252F%252Fimg16.slando.ua%252Fimages_slandocomua%252F74852745_1_644x461_podgotovka-k-zno-matematika-harkov.jpg%3Bhttp%253A%252F%252Fkharkov.kha.slando.ua%252Fobyavlenie%252Fpodgotovka-k-zno-matematika-ID5e1v1.html%3B527%3B461
