- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Площади многоугольников
Содержание
- 1. Площади многоугольников
- 2. ВведениеТема «Площади многоугольников» является неотъемлемой частью школьного
- 3. Что же такое площадь многоугольника?Площадь многоугольника –
- 4. Вычисление площадей в древностиВавилоняне еще 4-5 тысяч
- 5. Древний КитайЕсли брать во внимание Китай, то
- 6. Древний ЕгипетВ древнем Египте около 4000 лет
- 7. Единицы измерения площадейТакими мерами являются квадраты, стороны
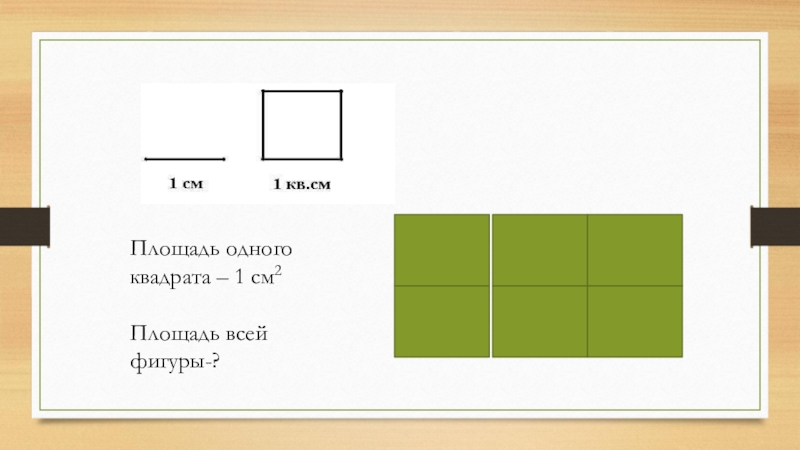
- 8. Площадь одного квадрата – 1 см2Площадь всей фигуры-?
- 9. Свойства площадейСвойство1. Равные многоугольники имеют равные площадиЗадачаПлощадь
- 10. Свойство 2. Если многоугольник составлен из нескольких
- 11. Найдите площадь данной фигурыДля того, чтобы найти
- 12. Слайд 12
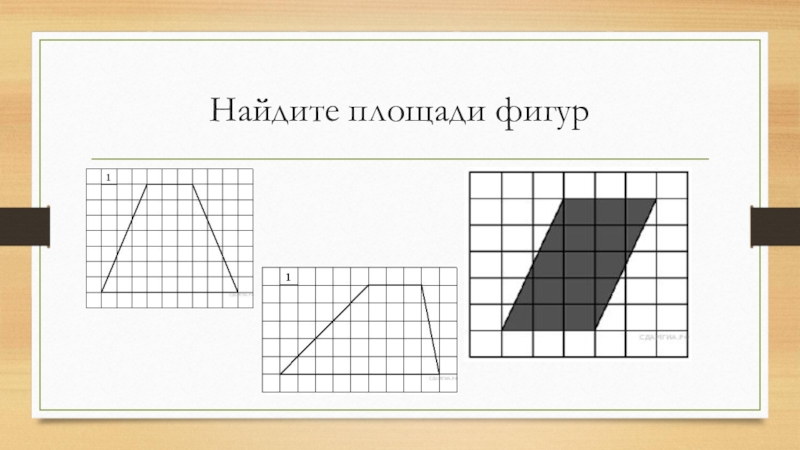
- 13. Найдите площади фигур
ВведениеТема «Площади многоугольников» является неотъемлемой частью школьного курса математики, что весьма логично. Ведь само возникновение геометрии связано с потребностью людей сравнивать земельные участки той или иной формы. В школьном курсе геометрии изучается множество различных способов нахождения
Слайд 2Введение
Тема «Площади многоугольников» является неотъемлемой частью школьного курса математики, что весьма
логично. Ведь само возникновение геометрии связано с потребностью людей сравнивать земельные участки той или иной формы. В школьном курсе геометрии изучается множество различных способов нахождения площадей геометрических фигур, которые часто применяются не только при решении математических задач, но и в повседневной жизни.
Слайд 3Что же такое площадь многоугольника?
Площадь многоугольника – это величина той части
фигуры. Которую занимает многоугольник.
Площадь многоугольника – выражается положительным числом.
Площадь многоугольника показывает сколько раз единица измерения или ее части укладываются в данном многоугольнике.
Площадь многоугольника – выражается положительным числом.
Площадь многоугольника показывает сколько раз единица измерения или ее части укладываются в данном многоугольнике.
Слайд 4Вычисление площадей в древности
Вавилоняне еще 4-5 тысяч лет назад умели определять
площадь прямоугольника и трапеции в квадратных единицах. С давних времен квадрат считался наиболее идеальной фигурой для измерения площадей.
Измерение производилось с помощью веревки. Геометрические познания вавилонян превышали египетские.
Измерение производилось с помощью веревки. Геометрические познания вавилонян превышали египетские.
Слайд 5Древний Китай
Если брать во внимание Китай, то стоит обратить свое внимание,
что там мерой площади являлся прямоугольник. Когда каменщики определяли площадь прямоугольной стены дома, они перемножали высоту и ширину стены. Отсюда и принятое в геометрии определение: площадь прямоугольника равна произведению его смежных сторон. Обе стороны должны быть выражены в одинаковых единицах измерения.
Слайд 6Древний Египет
В древнем Египте около 4000 лет назад пользовались похожими приемами,
что и мы, для измерения площади прямоугольника, треугольника и трапеции: основание треугольника делилось пополам, и умножалось на высоту; для трапеции же сумма параллельных сторон делилась пополам и умножалась на высоту.
Слайд 7Единицы измерения площадей
Такими мерами являются квадраты, стороны которых равны какой-нибудь линейной
мере: метру. дециметру, сантиметру. миллиметру.
При измерении площадей, имеющих большие размеры, за меру может быть принят квадрат, сторона которого равна километру.
Квадрат, сторона которого равна какой-нибудь линейной единице, называется квадратной единицей: квадратным метрам, квадратным сантиметром, квадратным километром и т.д.
Измерить площадь какой-либо геометрической фигуры – значит узнать, сколько тех или иных квадратных единиц содержится в фигуре, площадь которой измеряется.
При измерении площадей, имеющих большие размеры, за меру может быть принят квадрат, сторона которого равна километру.
Квадрат, сторона которого равна какой-нибудь линейной единице, называется квадратной единицей: квадратным метрам, квадратным сантиметром, квадратным километром и т.д.
Измерить площадь какой-либо геометрической фигуры – значит узнать, сколько тех или иных квадратных единиц содержится в фигуре, площадь которой измеряется.
Слайд 9Свойства площадей
Свойство1.
Равные многоугольники имеют равные площади
Задача
Площадь параллелограмма ABCD – 30
кв. см Чему равна площадь треугольника АВD?
Многоугольники, имеющие равные площади называются равновеликими.
Многоугольники, имеющие равные площади называются равновеликими.
Слайд 10Свойство 2.
Если многоугольник составлен из нескольких многоугольников, то его площадь
равна сумме площадей этих многоугольников.
S1=S2+S3
Если многоугольник разрезан на несколько многоугольников и из него составлен другой многоугольник, то такие многоугольники называют равносоставленными.
S1=S2+S3
Если многоугольник разрезан на несколько многоугольников и из него составлен другой многоугольник, то такие многоугольники называют равносоставленными.
Слайд 11Найдите площадь данной фигуры
Для того, чтобы найти площадь данной фигуры нужно
воспользоваться формулой Пика.
где В — количество целочисленных точек внутри многоугольника,
а Г — количество целочисленных точек на границе многоугольника
где В — количество целочисленных точек внутри многоугольника,
а Г — количество целочисленных точек на границе многоугольника
.