- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
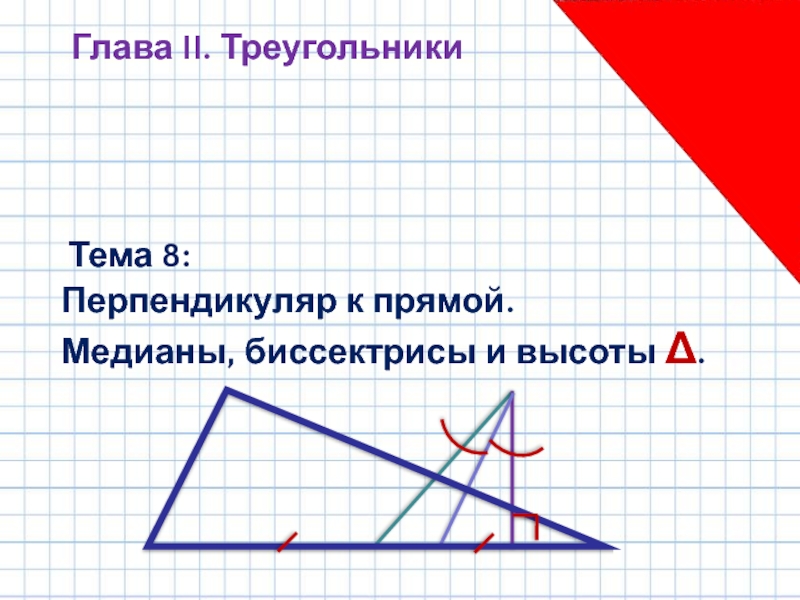
Презентация, доклад на тему Перпендикуляр к прямой. Медианы, биссектрисы и высоты
Содержание
- 1. Перпендикуляр к прямой. Медианы, биссектрисы и высоты
- 2. АТеорема: из точки, не лежащей на прямой,
- 3. Опр.: медиана Δ − это отрезок, соединяющий
- 4. Замечание: любой треугольник имеет 3 медианы, 3
- 5. 2. Биссектрисы Δ пересекаются в одной точке,
- 6. Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом! Анатоль Франс
Слайд 2А
Теорема: из точки, не лежащей на прямой, можно провести перпендикуляр к
Точка H называется основанием перпендикуляра.
Опр.: отрезок AH называется перпендикуляром к прямой a, если прямые AH и a перпендикулярны.
H
a
Д-во: 1) о существовании перпендикуляра для точки A ∉ a − прочитать в учебнике (стр. 32);
2) о единственности перпендикуляра. Предположим,
что можно провести ещё один перпендикуляр AH1 из точки A ∉ a к прямой a. Но тогда прямые AH⊥a и AH1⊥a пересекаются в точке A, что противоречит теореме о перпендикулярных прямых. Следовательно, перпендикуляр единственен.
Ч Т д
H1
Слайд 3
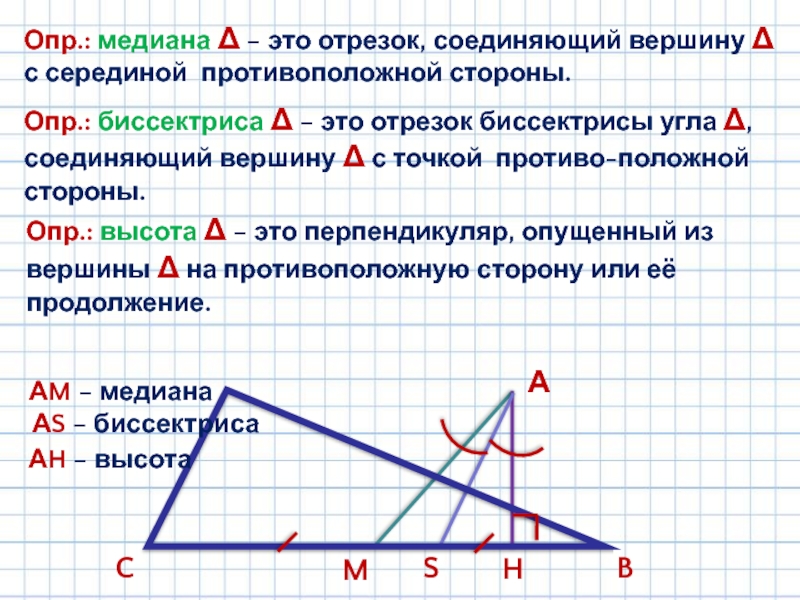
Опр.: медиана Δ − это отрезок, соединяющий вершину Δ с серединой
А
B
C
M
Опр.: биссектриса Δ − это отрезок биссектрисы угла Δ, соединяющий вершину Δ с точкой противо-положной стороны.
S
Опр.: высота Δ − это перпендикуляр, опущенный из вершины Δ на противоположную сторону или её продолжение.
H
АM − медиана
АS − биссектриса
АH − высота
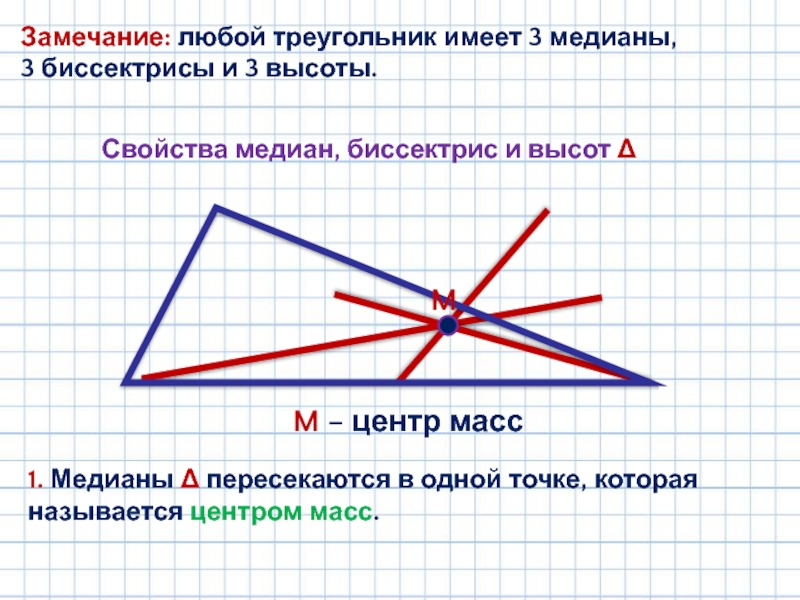
Слайд 4Замечание: любой треугольник имеет 3 медианы,
3 биссектрисы и 3 высоты.
Свойства
1. Медианы Δ пересекаются в одной точке, которая называется центром масс.
M
M − центр масс
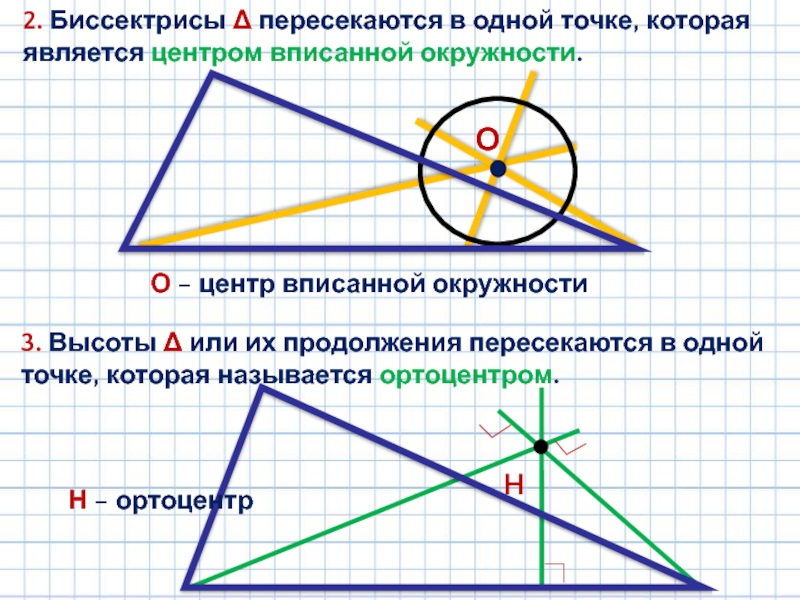
Слайд 52. Биссектрисы Δ пересекаются в одной точке, которая является центром вписанной
О − центр вписанной окружности
О
3. Высоты Δ или их продолжения пересекаются в одной точке, которая называется ортоцентром.
H
Н − ортоцентр
Слайд 6
Учиться можно только весело… Чтобы переваривать знания, надо поглощать
Анатоль Франс