- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Ортогональная проекция многоугольника и ее площадь
Содержание
- 1. Ортогональная проекция многоугольника и ее площадь
- 2. Задача № 1Большее основание равнобедренной трапеции, принадлежит
- 3. Виды проектирования:центральное параллельноеПрямоугольное(ортогональное)косоугольное
- 4. Свойства ортогонального проектированияПроекцией прямой является прямая.Проекцией параллельных
- 5. Ортогональная проекция фигуры на плоскость:lBAαB1A1A1 B1 – ортогональная проекция АВ на α
- 6. Ортогональная проекция фигуры на плоскость:lABCαA1B1C1Δ А1 В1 С1 – ортогональная проекция Δ АВС на плоскостьα
- 7. ΔАВС и ΔА1 В1 С1 могут быть
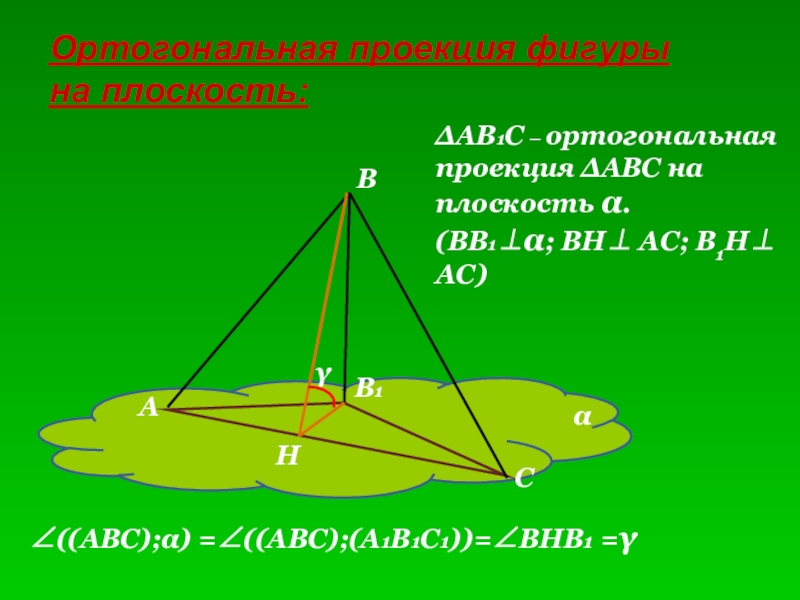
- 8. Ортогональная проекция фигуры на плоскость:ВАСВ1αНγΔАВ1С – ортогональная
- 9. S ΔAB1C =S ΔABC ⋅ cosγПлощадь ортогональной
- 10. ВАСВ1αНγΔАВ1С – ортогональная проекция ΔАВС на плоскость α.(ВВ1⊥α; ВН⊥ АС; В1Н⊥ АС)∠((АВС);α) =∠((АВС);(А1В1С1))=∠ВНВ1 =γ
- 11. Через сторону АС = 10 см равностороннего
- 12. Ортогональной проекцией треугольника, площадь которого 420 является
- 13. Задание на дом:П. 34, №№ 48, 49(1)
Задача № 1Большее основание равнобедренной трапеции, принадлежит плоскости α, которая с плоскостью трапеции образует угол 60°. Зная, что основания трапеции 15 см и 5 см, а боковая сторона 5 см, найти расстояние между меньшим основанием
Слайд 2Задача № 1
Большее основание равнобедренной трапеции, принадлежит плоскости α, которая с
плоскостью трапеции образует угол 60°. Зная, что основания трапеции 15 см и 5 см, а боковая сторона 5 см, найти расстояние между меньшим основанием и плоскостью α и угол между диагональю трапеции и плоскостью α.
Слайд 4Свойства ортогонального
проектирования
Проекцией прямой является прямая.
Проекцией параллельных прямых
являются параллельные
прямые.
Сохраняется отношение отрезков, лежащих на параллельных прямых.
Сохраняется отношение отрезков, лежащих на параллельных прямых.
Слайд 6Ортогональная проекция фигуры
на плоскость:
l
A
B
C
α
A1
B1
C1
Δ А1 В1 С1 – ортогональная проекция
Δ АВС на плоскостьα
Слайд 7ΔАВС и ΔА1 В1 С1 могут быть равны,
а могут быть и
не равны.
РАВНЫ: если (АВС)⏐⏐ α.
НЕ РАВНЫ: если угол между их
плоскостями 0°< γ <90°.
РАВНЫ: если (АВС)⏐⏐ α.
НЕ РАВНЫ: если угол между их
плоскостями 0°< γ <90°.
Ортогональная проекция фигуры
на плоскость:
Слайд 8Ортогональная проекция фигуры
на плоскость:
В
А
С
В1
α
Н
γ
ΔАВ1С – ортогональная
проекция ΔАВС на
плоскость
α.
(ВВ1⊥α; ВН⊥ АС; В1Н⊥ АС)
(ВВ1⊥α; ВН⊥ АС; В1Н⊥ АС)
∠((АВС);α) =∠((АВС);(А1В1С1))=∠ВНВ1 =γ
Слайд 9S ΔAB1C =S ΔABC ⋅ cosγ
Площадь ортогональной проекции
треугольника равна произведению площади
треугольника
на косинус угла между их
плоскостями.
плоскостями.
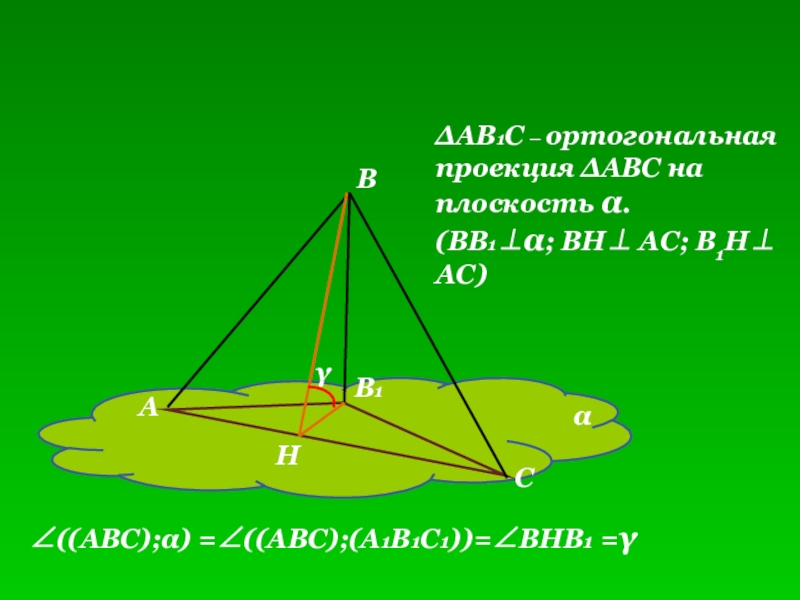
Слайд 10
В
А
С
В1
α
Н
γ
ΔАВ1С – ортогональная
проекция ΔАВС на
плоскость α.
(ВВ1⊥α; ВН⊥ АС; В1Н⊥
АС)
∠((АВС);α) =∠((АВС);(А1В1С1))=∠ВНВ1 =γ
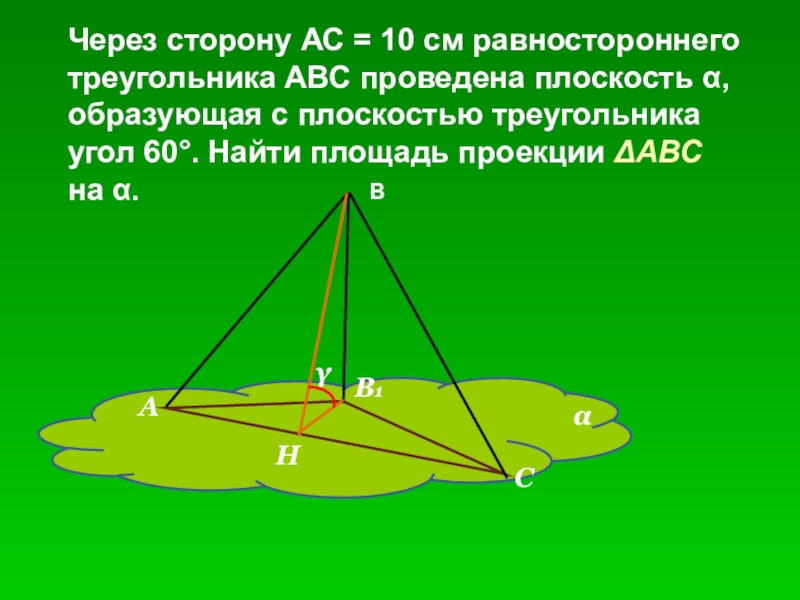
Слайд 11Через сторону АС = 10 см равностороннего
треугольника АВС проведена плоскость
α,
образующая с плоскостью треугольника
угол 60°. Найти площадь проекции ΔАВС
на α.
образующая с плоскостью треугольника
угол 60°. Найти площадь проекции ΔАВС
на α.
А
С
В1
α
Н
γ
В
Слайд 12Ортогональной проекцией треугольника,
площадь которого 420 является
треугольник со сторонами 39;
17; 28 см.
Найдите угол между плоскостями.
Дополнительно:
В правильной пирамиде боковое ребро
6 см наклонено к плоскости основания
под углом 60°. Найти периметр
основания, площадь основания.
Найдите угол между плоскостями.
Дополнительно:
В правильной пирамиде боковое ребро
6 см наклонено к плоскости основания
под углом 60°. Найти периметр
основания, площадь основания.