математики МКОУ СШ № 2
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Нестандартные приёмы решения задач ЕГЭ по стереометрии
Содержание
- 1. Нестандартные приёмы решения задач ЕГЭ по стереометрии
- 2. Задача 1сделаем дополнительные построения
- 3. достроим до параллелепипедаГде будет лежать центр описанной
- 4. 2 точки у нас есть, нужна точка
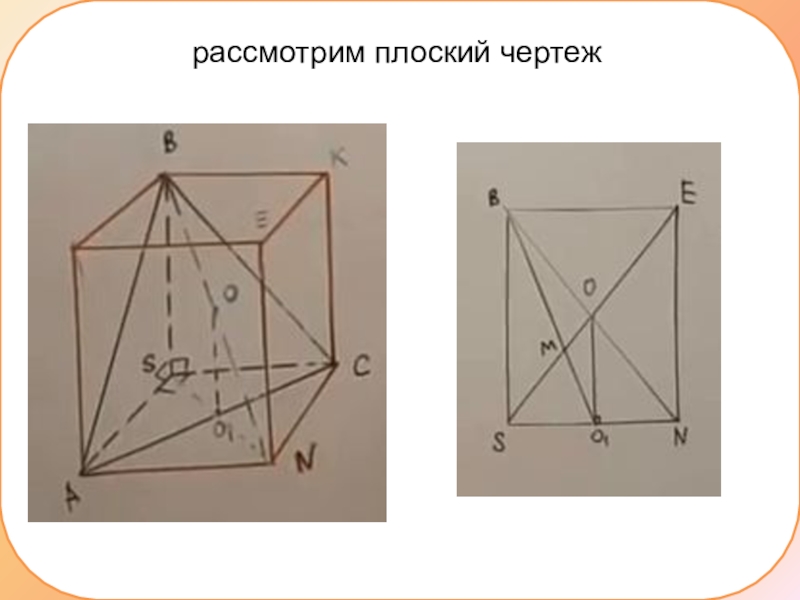
- 5. рассмотрим плоский чертеж
- 6. Слайд 6
- 7. б) найдем радиус сферы вписанной в эту пирамидуВ каком случае сфера вписана в пирамиду?
- 8. б) найдем радиус сферы вписанной в эту
- 9. б) найдем радиус сферы вписанной в эту
- 10. Слайд 10
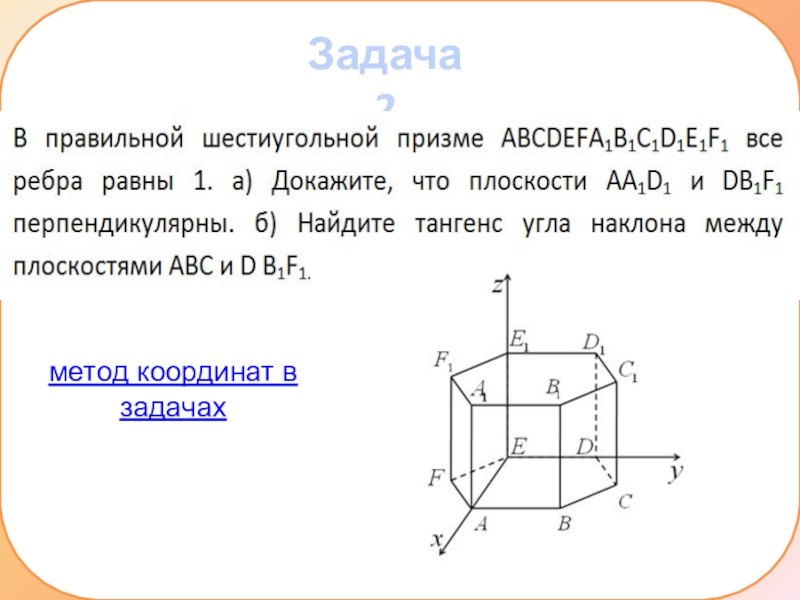
- 11. Задача 2метод координат в задачах
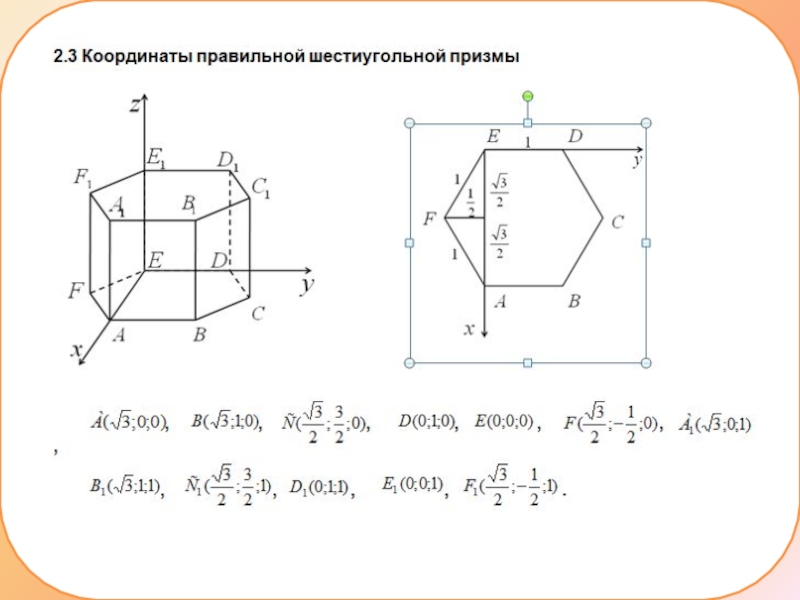
- 12. Слайд 12
- 13. Немного теорииуравнение плоскостиугол между двумя плоскостямиесли cos ᵩ = 0, то плоскости будут перпендикулярны.
- 14. Немного теориисоставим уравнение плоскостисоставим уравнение плоскости
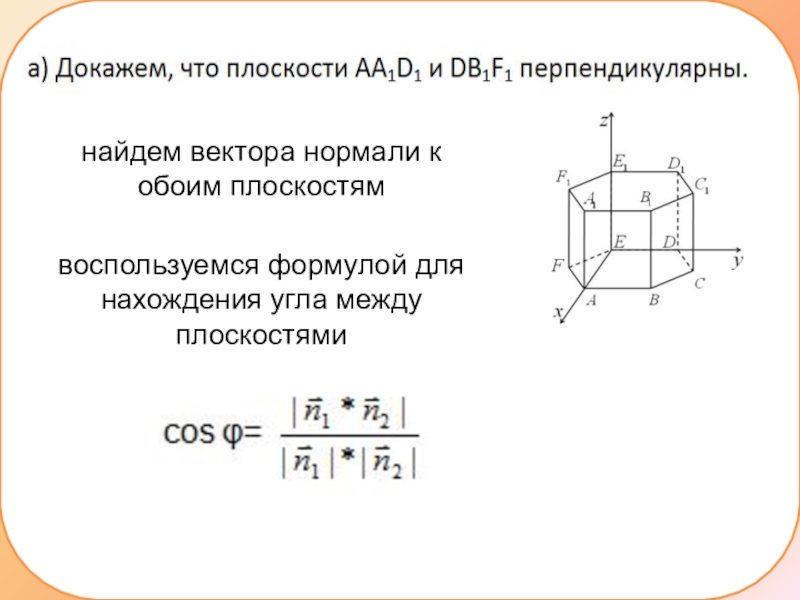
- 15. найдем вектора нормали к обоим плоскостямвоспользуемся формулой для нахождения угла между плоскостями
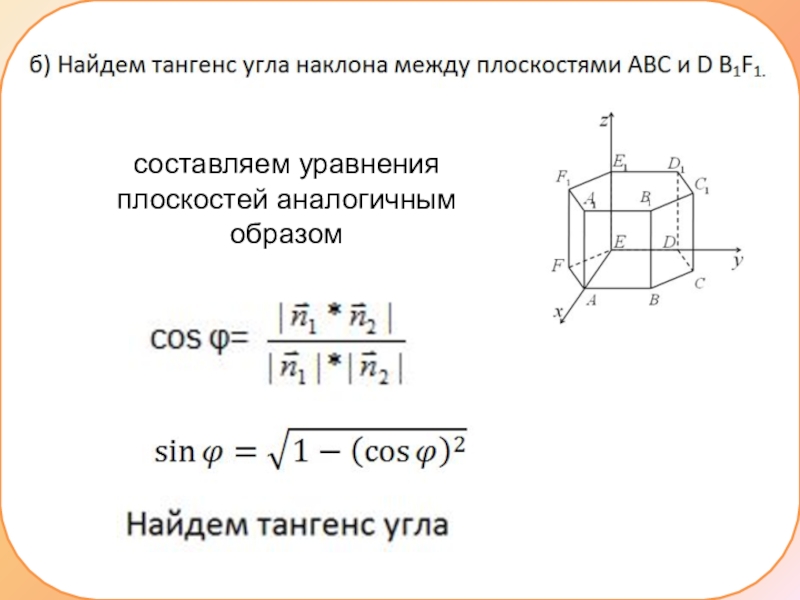
- 16. составляем уравнения плоскостей аналогичным образом
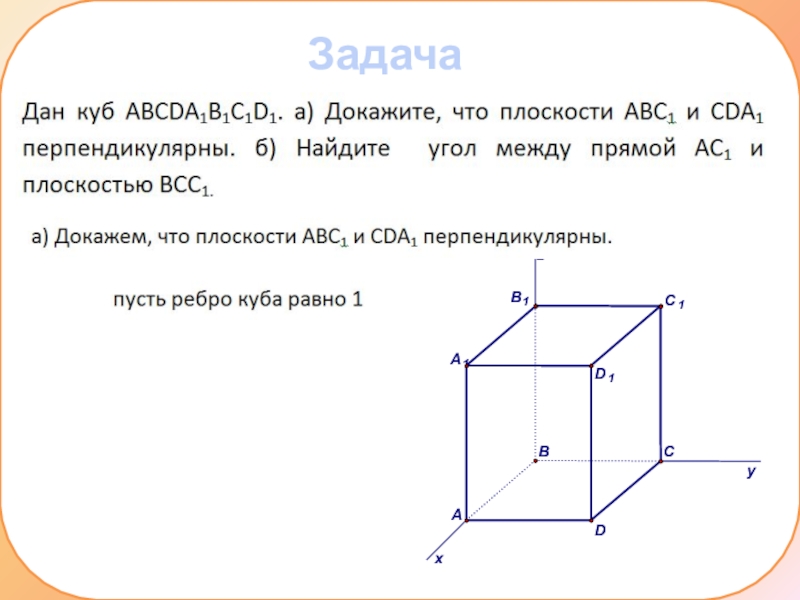
- 17. Задача 3
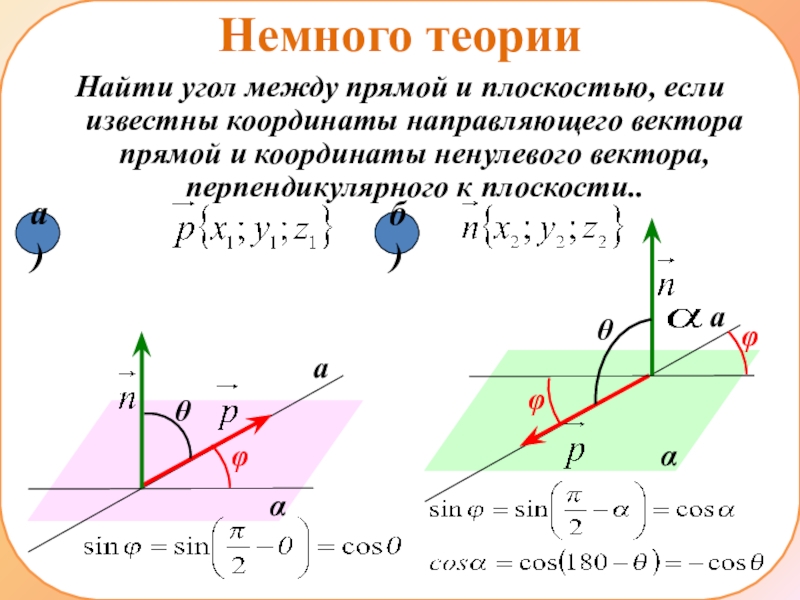
- 18. Немного теорииНайти угол между прямой и плоскостью,
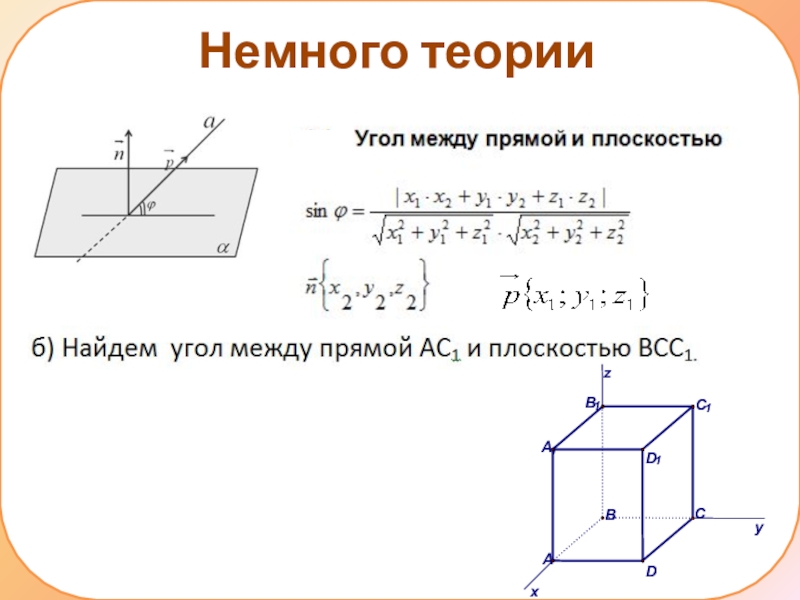
- 19. Немного теории
- 20. Задачи для самостоятельного решения
- 21. Задачи для самостоятельного решения
- 22. Спасибо за внимание!
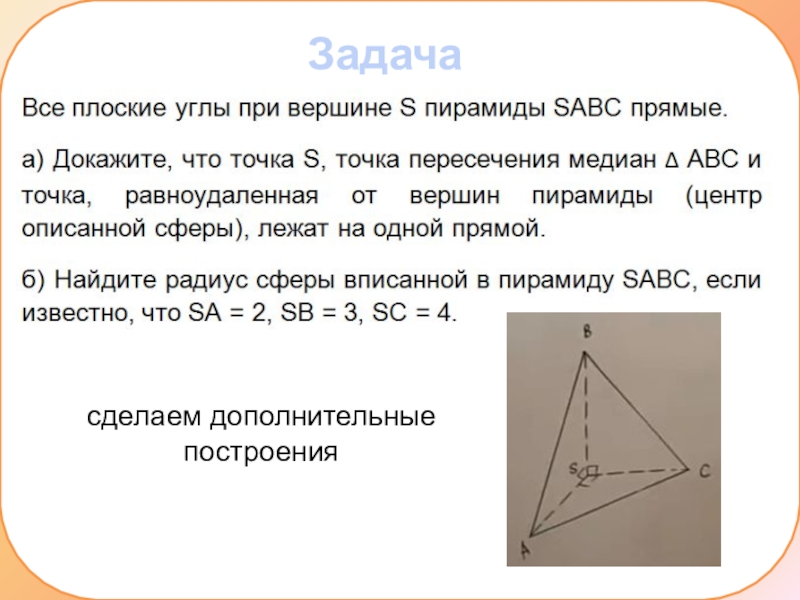
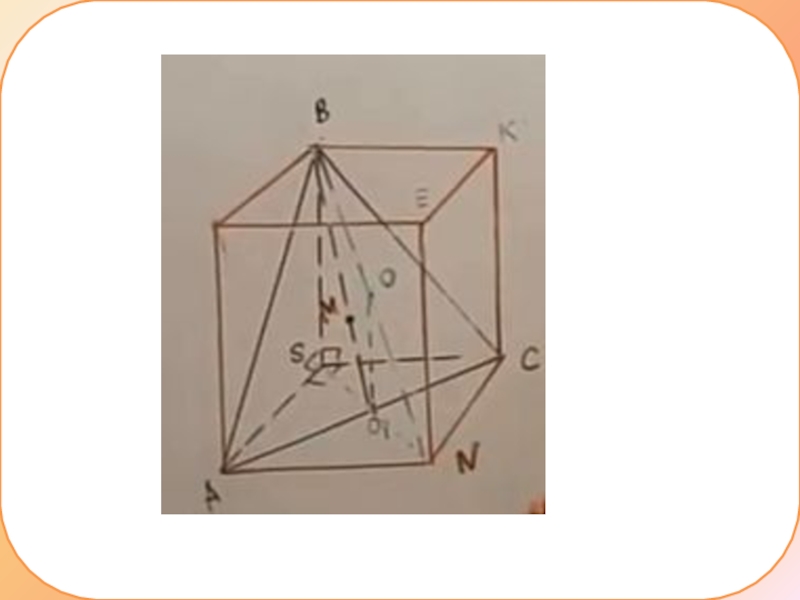
Задача 1сделаем дополнительные построения
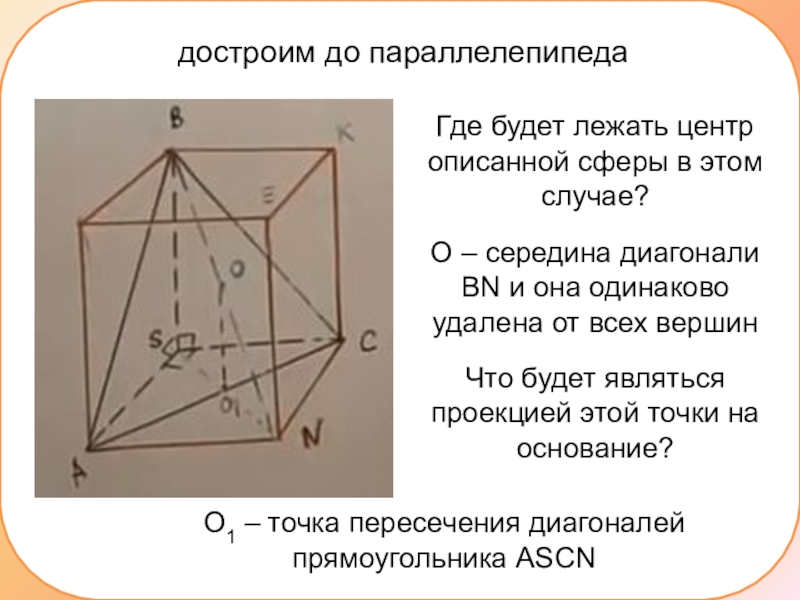
Слайд 3достроим до параллелепипеда
Где будет лежать центр описанной сферы в этом случае?
О
– середина диагонали ВN и она одинаково удалена от всех вершин
Что будет являться проекцией этой точки на основание?
О1 – точка пересечения диагоналей прямоугольника АSCN
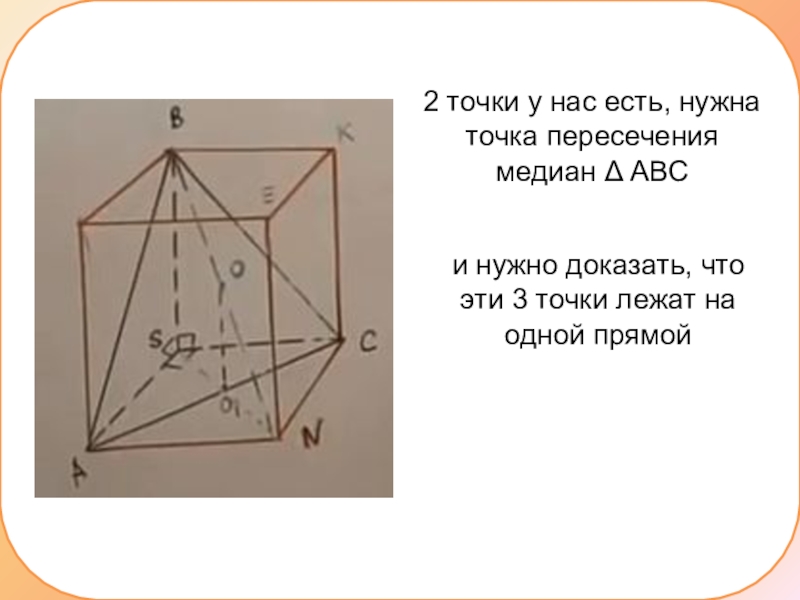
Слайд 42 точки у нас есть, нужна точка пересечения медиан Δ АВС
и
нужно доказать, что эти 3 точки лежат на одной прямой
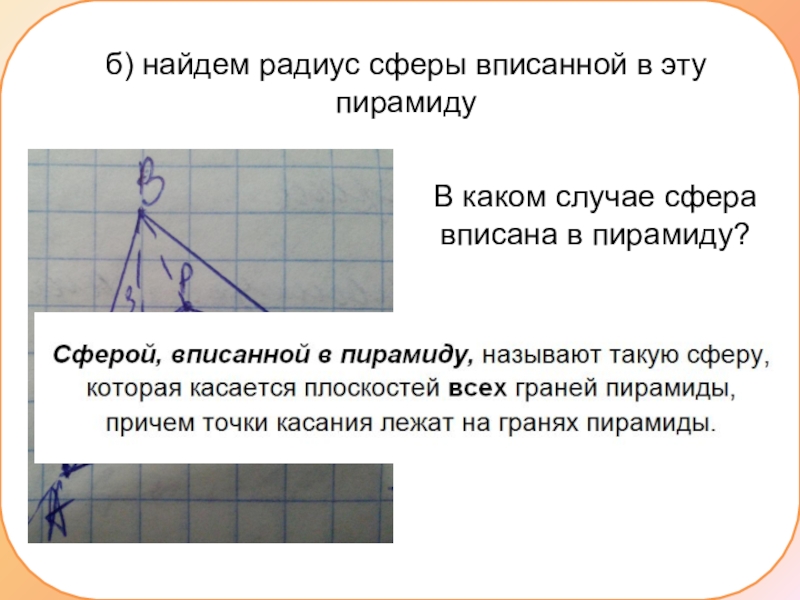
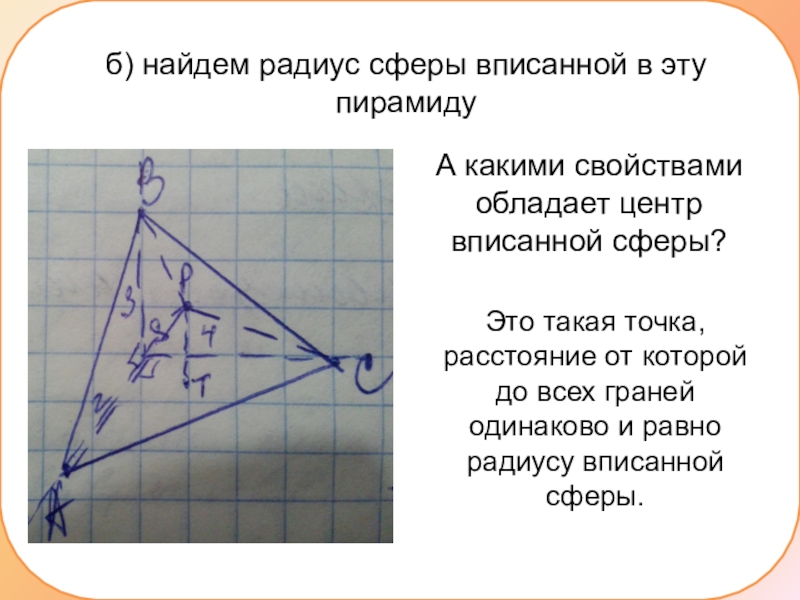
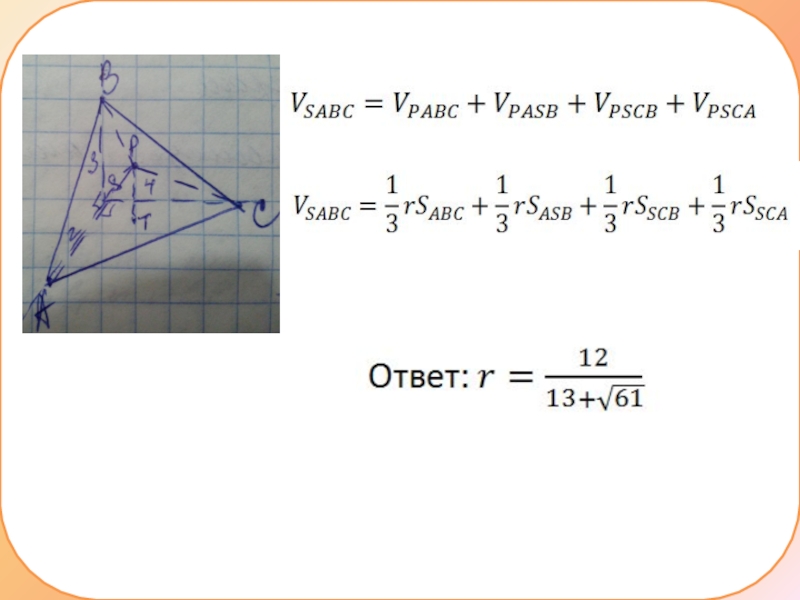
Слайд 8б) найдем радиус сферы вписанной в эту пирамиду
А какими свойствами обладает
центр вписанной сферы?
Это такая точка, расстояние от которой до всех граней одинаково и равно радиусу вписанной сферы.
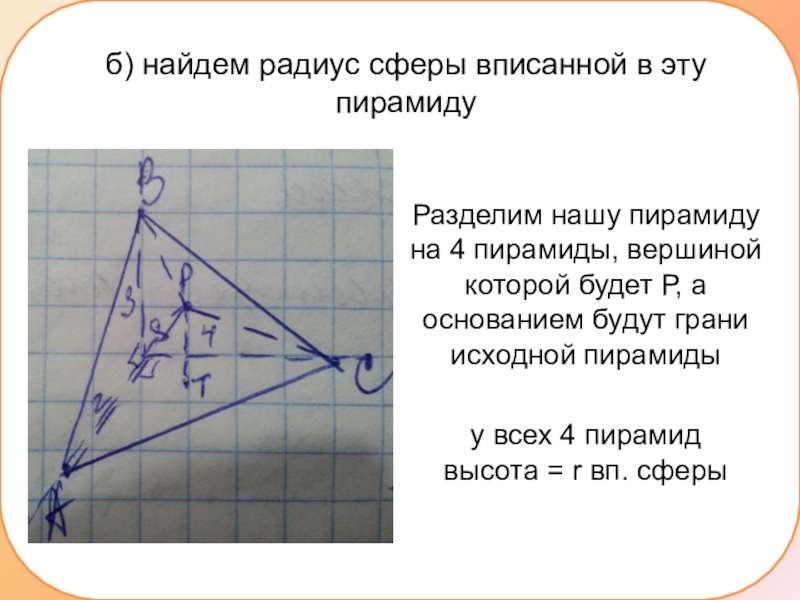
Слайд 9б) найдем радиус сферы вписанной в эту пирамиду
Разделим нашу пирамиду на
4 пирамиды, вершиной которой будет Р, а основанием будут грани исходной пирамиды
у всех 4 пирамид высота = r вп. сферы
Слайд 13Немного теории
уравнение плоскости
угол между двумя плоскостями
если cos ᵩ = 0, то
плоскости будут перпендикулярны.
Слайд 15найдем вектора нормали к обоим плоскостям
воспользуемся формулой для нахождения угла между
плоскостями
Слайд 18Немного теории
Найти угол между прямой и плоскостью, если известны координаты направляющего
вектора прямой и координаты ненулевого вектора, перпендикулярного к плоскости..
а)
б)
α
а
φ
θ
α
а
φ
φ
θ