- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Методы решения геометрической задачи
Содержание
- 1. Методы решения геометрической задачи
- 2. 1 способ. Используя определение. Найти
- 3. Проведем DH⊥АС, следовательно по тереме о трех
- 4. 2 способ. Метод объемов (использование вспомогательной
- 5. Прямоугольный параллелепипед — параллелепипед, все грани которого
- 6. :Ответ: Вычислим площадь треугольника ACD Вычислим площадь треугольника АСD1, используя формулу Герона Ответ: . Ответ: .
- 7. 3 способ. Координатный метод. Пусть
- 8. Уравнение плоскости ACD1 примет вид Пусть aх+by+cz+d=0 –
- 9. 4 способ. Векторный метод. Введем базис (рис. 4) , .
- 10. Поэтому Далее имеем: ак к имее: : Ответ:
Слайд 2
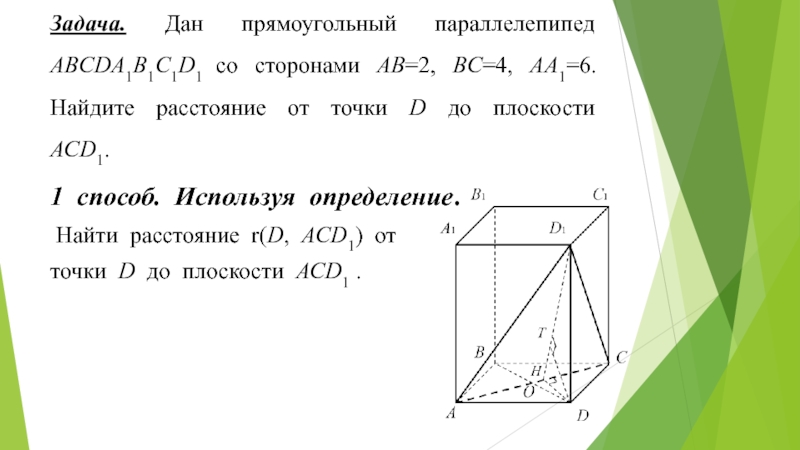
1 способ. Используя определение.
Найти расстояние r(D, АСD1) от
точки
Задача. Дан прямоугольный параллелепипед АBСDA1B1C1D1 со сторонами AB=2, BC=4, AA1=6. Найдите расстояние от точки D до плоскости АСD1.
Слайд 3Проведем DH⊥АС, следовательно по тереме о трех перпендикулярах D1H⊥АС и (DD1H)⊥АС. Проведем
Из прямоугольного треугольника D1DH найдем гипотенузу D1H и высоту DT
Ответ:
.
Слайд 4
2 способ. Метод объемов
(использование вспомогательной пирамиды).
Задачи данного типа можно свести
Слайд 5Прямоугольный параллелепипед — параллелепипед, все грани которого являются прямоугольниками. AB=CD=2, BC=AD=4, AA1=6. Искомым
Вычисляя, вторым способом за основание примем ∆ ACD, тогда
Приравняем правые части последних двух равенств, получим
Из прямоугольных треугольников АСD, ADD1, CDD1 найдем гипотенузы, используя теорему Пифагора
Слайд 6:
Ответ:
Вычислим площадь треугольника ACD
Вычислим площадь треугольника АСD1, используя формулу Герона
Ответ:
.
Ответ:
.
Слайд 73 способ. Координатный метод. Пусть дана точка M(x0,y0,z0) и плоскость α,
Слайд 8Уравнение плоскости ACD1 примет вид
Пусть aх+by+cz+d=0 – уравнение плоскости ACD1.
Подставляя